
2020中考数学线段最值问题之阿波罗尼斯圆(阿氏圆)
【知识背景】
阿波罗尼斯与阿基米德、欧几里德齐名,被称为亚历山大时期数学三巨匠。阿波罗尼斯对圆锥曲线有深刻而系统的研究,其主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是其研究成果之一,本文主要讲述阿波罗尼斯圆在线段最值中的应用,下文中阿波罗尼斯圆简称为“阿氏圆”。
【定 义】
阿氏圆是指:平面上的一个动点P 到两个定点A ,B 的距离的比值等于k ,且k≠1的点P 的轨迹称之为阿氏圆。即:
)1(≠=k k PB
PA
,如下图所示:
上图为用几何画板画出的动点P 的轨迹,分别是由图中红色和蓝色两部分组成的的圆,由于是静态文档的形式,无法展示动图,有兴趣的可以用几何画板试一试。
【几何证明】
证明方法一:初中纯几何知识证明:阿氏圆在高中数学阶段可以建立直角坐标系,用解析几何的方式来确定其方程。但在初中阶段,限于知识的局限性,我们可以采用纯几何的证明方式,在证明前需要先明白角平分线定理及其逆定理,请看下文: 知识点1:内角平分线定理及逆定理
若AD 是∠BAC 的角平分线,则有:
CD
BD
AC AB =
。即“两腰之比”等于“两底边之比”。 其逆定理也成立:即CD
BD
AC AB =
,则有:AD 是∠BAC 的角平分线。
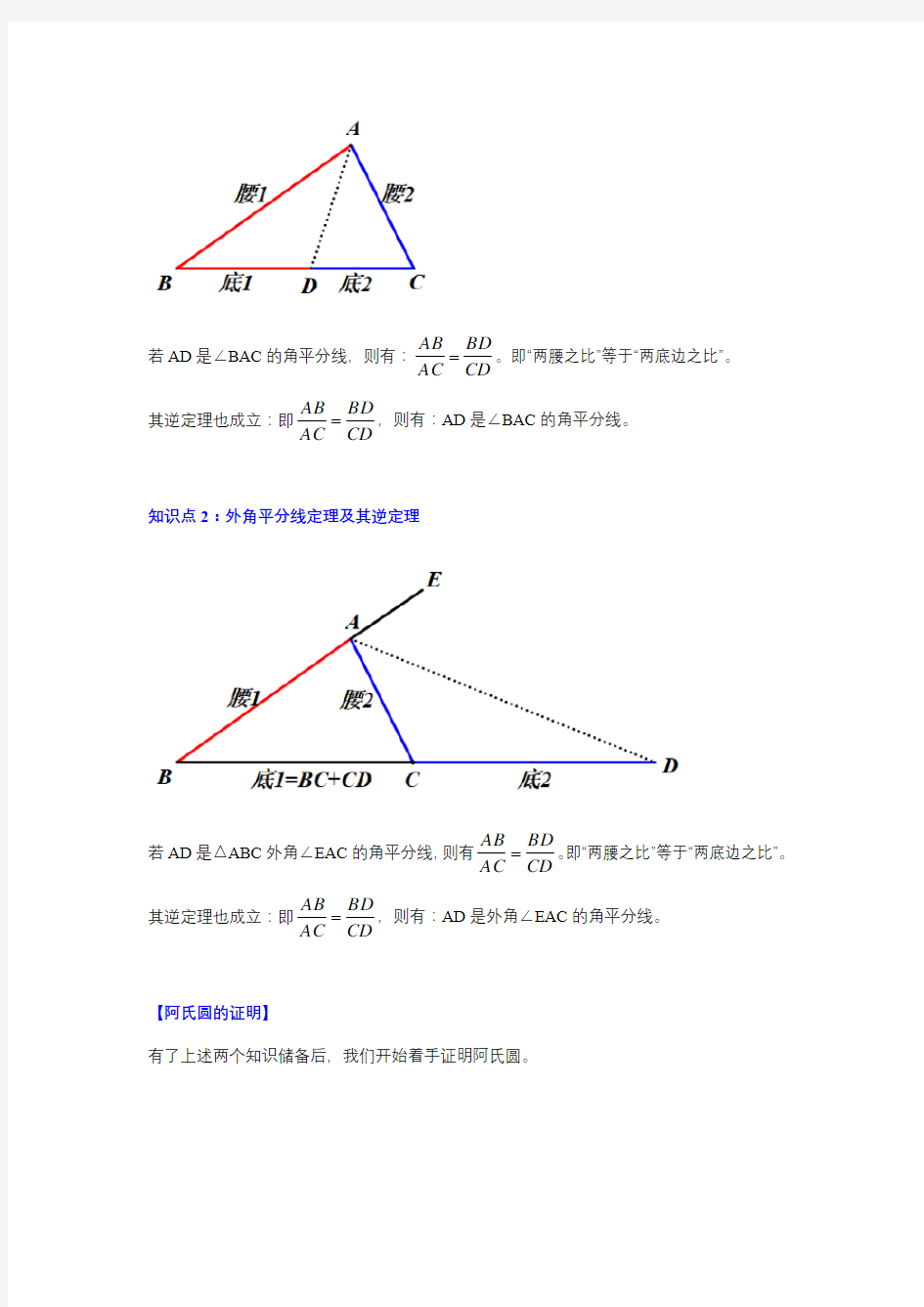
知识点2:外角平分线定理及其逆定理
若AD 是△ABC 外角∠EAC 的角平分线,则有
CD
BD
AC AB =
。即“两腰之比”等于“两底边之比”。 其逆定理也成立:即CD
BD
AC AB =
,则有:AD 是外角∠EAC 的角平分线。
【阿氏圆的证明】
有了上述两个知识储备后,我们开始着手证明阿氏圆。
①如上图,根据阿氏圆的定义: 当P 点位于图中P 点位置时有:
k PB PA =,当P 点位于图中N 点位置时有:k NB
NA
=, 所以有:
NB
NA
PB PA =
,所以PN 是∠APB 的角平分线,∴∠1=∠2. 当P 点位于图中M 点位置时有:
PB
PA
k MB MA =
=, 所以有:
MB
MN
PB PA =
,所以PM 是∠EPA 的角平分线,∴∠3=∠4. 又∵∠1+∠2+∠3+∠4=180° ∴2∠1+2∠3=180° ∴∠1+∠3=90°
故∠MPN=90°,所以动点P 是在以MN 为直线的圆上。
② 由上述过程,我们可以更进一步推导出阿氏圆的直径,设定点间距离AB=a , ∵
k MB
MA
=,
∴k
MA
MB =
∵MB - MA = a ∴
a MA k
MA
=- ∴.1k
ak
MA -=
同理,∵
k NB
NA
= ∴k
NA
NB =
∵NA+NB=a ∴k
NA
NA +
=a
∴1
+=
k ak
NA ∴直径|
1|2112k ak
k ak k ak NA MA MN -=++-=
+=。
证明方法二:高中解析几何建立直角坐标系,如下图所示
以定直线AB 所在直线为x 轴,点A 为坐标原点,建立平面直角坐标系,设AB=a ,则A(0,0), B(a,0),设P(x,y),则
k PB
PA
=,即 k y
a x y x =+-+2
2
22)(,两边平方,整理得:
02)1()1(2222222=+--+-a k x ak y k x k ,又k ≠1,配方得:
2
2222
222)1()1(-=+--k a k y k ak x
由圆的方程可知:此方程表示是以)0,1(22-k ak 为圆心,|
1|2-k ak
为半径的圆。
【实际应用】
阿氏圆常用于解决形如:)1(≠?+k PB k PA 类线段最值问题:其中P 是动点,A ,B 是定点,且动点P 在阿氏圆上运动(这和我上一讲中的P 点在直线上动产生的胡不归有本质区别)。 先看如下例题,然后我们总结出更加一般的解题步骤,使这种题变成套路题,直接秒杀。
【例题1】如下图1,已知圆O 的半径r=4,A(6,0),B 是圆上一动,在x 轴上取一点M ,使得△OBM ∽△OAB 。
(1)求M 点的坐标并求出相似比;
(2)在(1)的条件下,若C 点的坐标为(0,5),求AB BC 3
2
+
的最小值。
分析:(1)△OBM 与△OAB 中有公共角∠BOA ,此题由于B 点动导致两个三角形中的其他角都在动,故从角角相等去判定相似有难度,但题目中给出的已知条件都是边,所以从边对
应成比例及夹角相等去判定会简单一些。 在x 轴上选择点M ,使得
OB
OM
OA OB =
,且∠BOA 是公共角,所以此时△OBM ∽△OAB 。 ∴OB 2=OA ×OM (即构造共边共角模型:共边的平方等于从共顶点出发两线段的乘积) ∴42=6×OM ,∴OM=
38,∴M 坐标为)0,38(,此时相似比为:3
2===AB BM OB OM OA OB . (2) 由(1)中相似知:
32=AB BM ,
∴
BM AB =3
2
∴BM BC AB BC +=+
3
2
,由两点之间线段最短可知: 3
17
)38(52222=+=+==+OM OC CM BM BC 。
∴AB BC 32+的最小值为3
17
。
【方法总结】
从上面例1中我们可以得到)1(≠?+k PB k PA 类问题更加一般性的解题步骤:
运用:动点在圆上运动,两线段(带系数)相加求最小值。 形如:AB+k ×BP 的最小值 (k 为系数),
原理:构造共边共角相似,转移带系数的边,利用两点间线段最短求最小值, 解题步骤:
Step1: 计算出动点所在圆的半径r ;
Step2:在题中寻找:
k r
=定边
(相似比),若找不到,则需要将系数k 提到括号外
边再寻找相似比;比如PB PA 5
3
+
,找不到相似比为3:5时,需要经过如下变形: )3
5
(5353PB PA PB PA +=+,对带系数的线段PA 去寻找相似比为5:3。
Step3:利用共边共角模型,在第2步:定边所在的三角形中构造共边共角相似模型,此时定边与动点构成一个三角形(此步非常重要,是核心);
Step4:利用相似转移带系数的边; Step5:由两点间线段最短求最小值。
【例题2】已知如下图1所示,圆O 的半径r=4,A(6,0),C(0,5),B 为圆上一动点。求BC AB 5
4
+的最小值。
分析:按照上述的解题步骤,此题变成了套路题: Step1:计算出动点所在圆的半径,题目直接已知r=4;
Step2:在题中寻找:
5
4
=定边r ,此题中的定边有:OA=6,OC=5,显然选择定边为OC ; Step3:在OC 边所在的三角形中构造共边共角相似模型,如上图2: 在y 轴上选取点M ,并使得:
OB
OM
OC OB =
,且有∠COB 是公共角, ∴△OMB ∽△OBC ,由共边共角模型知道:OM OC OB ?=2
(共边的平方等于从共顶点出发两条线段的乘积),∴16=5·OM ,∴OM=5
16。 Step4:利用相似转移带系数的边; 此时由构造出的△OMB ∽△OBC 可知:54==OC OB BC BM ,∴BC BM 5
4
=。 Step5:由两点间线段最短求最小值。 ∴BC AB 5
4
+
=BM AB +,由两点之间线段最短可知,其最小值为AM : BM AB +.5
34)516(
62222=+=+==OM AO AM
【例题3】如下图1,已知B(12,0),A(0,12),D(10,0),C 为OA 的中点,P 为圆O 上一动点,求PD PC 2
1
+
的最小值。
分析:按照上述的解题步骤,此题变成了套路题:
Step1:计算出动点所在圆的半径,题目直接已知r=OB=12;
Step2:在题中寻找:
2
1
=定边r ,此题中的定边有:OA=OB=12,OC=AC=6,显然没有21=定边r ,所以必须要提取21出来,∴)2(21
21PD PC PD PC +=+,再去寻找:1
2
=定边r ,显然OC=6,故应选择定边OC. Step3:在OC 边所在的三角形中构造共边共角相似模型,如上图2:
在y 轴上选取点M ,并使得:
OP
OC
OM OP =
,且有∠MOP 是公共角, ∴△OCP ∽△OPM ,由共边共角模型知道:OM OC OP ?=2
(共边的平方等于从共顶点出发两条线段的乘积),∴122=6·OM ,∴OM=24。 Step4:利用相似转移带系数的边; 此时由构造出的△OCP ∽△OPM 可知:1
2
===PC PM OP OM OC OP ,∴PC PM 2=。 Step5:由两点间线段最短求最小值。 ∴)(2
1
)2(2121PD PM PD PC PD PC +=+=+
,由两点之间线段最短可知,其最小值为: .13262
12121)(2122=?=+==+OM OD MD PD PM
【课后演练】
1、如图,直角坐标系中,AB=5,AO=3,圆O 的半径为2,P 为圆O 上一个动点, (1) 求PB PA 2
1
+
的最小值是__________. (2) 求
PB PA +3
2
的最小值是_________.
【答案】(1)10
(2)
3
10
4 2、如图,A(-1,0),B(1,0),C(-1,1), D (1,3),P 点在以AB 为直径的圆上,则PD PC 2 的最小值是__________。
【答案】
2
34
3、如图,在扇形COD 中,OC=4,OA=2,OB=3,∠COD=120°,P 是弧BC 上一动点,不与D 、C 重合,则2PA+PB 的最小值是_______。
【答案】97
4、如图,等边△ABC 的边长为6,内切圆记为圆O ,P 是圆O 上一动点,则2PC+PB 的最小值为_______。
【答案】73
5、如图,在等边△ABC 中,AB=12,圆C 的半径为6,P 是圆上一动点,连接AP ,BP ,则BP AP 2
1
的最小值是________。
【答案】133
6、如图1,抛物线)0(2)2(2
≠+++=a a x a ax y 与x 轴交于A(4,0),与y 轴交于点B ,在x 轴上有一动点P(m ,0),过点P 作x 轴垂线交AB 于N ,交抛物线于点M 。 (1) 求a 的值;
(2) 若PN:MN=1:3,求m 的值;
(3) 如图(2),在(2)的条件下,设动点P 对应的位置是P 1,将线段OP 1绕点O 逆时钟旋转得到OP 2,旋转角度为α,且0<α<90°,连接AP 2、BP 2,求222
3
BP AP +
的最小值。
【答案】 (1) 22
3
212++-
=x x y (2) 3=m
(3)
2
145
7、如图1,在平面直角坐标系中,点M 的坐标为(3,0),以点M 为圆心,5为半径的圆与坐标轴分别交于点A 、B 、C 、D . (1)△AOD 与△COB 相似吗?为什么?
(2)如图2,弦DE 交x 轴于点P ,且BP :DP=3:2,求tan△EDA ;
(3)如图3,过点D 作△M 的切线,交x 轴于点Q .点G 是△M 上的动点,问比值
GQ
GO
是否变化?若不变,请求出比值;若变化,请说明理由.
【答案】 (1)相似
(2)
3
11 (3)不变,其值为
5
3
(本质为阿氏圆,QO 为定直线,G 为动点
53 GQ GO )。
阿氏圆题型的解题方法和技巧 以阿氏圆(阿波罗尼斯圆)为背景的几何问题近年来在中考数学中经常出现,对于此类问题的归纳和剖析显得非常重要. 具体内容如下: 阿氏圆定理(全称:阿波罗尼斯圆定理),具体的描述:一动点P 到两定点A、B的距离之比等于定比 n m (≠1),则P 点的轨迹,是以定比n m 内分和外分定线段AB 的两个分点的连线为直径的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现,该圆称为阿波罗尼斯圆,简 称阿氏圆. 定理读起来和理解起来比较枯燥,阿氏圆题型也就是大家经常见到的PA+kPB,(k ≠1)P 点的运动轨迹是圆或者圆弧的题型. PA +kPB,(k≠1)P 点的运动轨迹是圆或圆弧的题型 阿氏圆基本解法:构造母子三角形相似 【问题】在平面直角坐标系xOy 中,在x 轴、y 轴分别有点C(m,0),D(0,n).点P 是平面内一动点,且OP=r,求P C+kPD 的最小值. 阿氏圆一般解题步骤: 第一步:确定动点的运动轨迹(圆),以点O为圆心、r 为半径画圆;(若圆已经画出则可省略这一步) 第二步:连接动点至圆心O(将系数不为1的线段的固定端点与圆心相连接),即连接O P、OD; 第三步:计算出所连接的这两条线段OP 、OD 长度; 第四步:计算这两条线段长度的比k ; 第五步:在OD 上取点M ,使得O M:OP =OP:OD=k; 第六步:连接CM,与圆O 交点即为点P .此时CM 即所求的最小值. 【补充:若能直接构造△相似计算的,直接计算,不能直接构造△相似计算的,先把k 提到括号外边,将其中一条线段的系数化成 k 1 ,再构造△相似进行计算】
阿波罗尼斯圆及其应用 数学理论 1.“阿波罗尼斯圆”:在平面上给定两点B A ,,设P 点在同一平面上且满足,λ=PB PA 当0>λ且1≠λ时,P 点的轨迹是个圆,称之为阿波罗尼斯圆。 (1=λ时P 点的轨迹是线段AB 的中垂线) 2.阿波罗尼斯圆的证明及相关性质 定理:B A ,为两已知点,Q P ,分别为线段AB 的定比为)1(≠λλ的内外分点,则以PQ 为直径的圆O 上任意点到B A ,两点的距离之比为.λ 证 (以1>λ为例) 设λ===QB AQ PB AP a AB ,,则 1 ,1,1,1-=-=+=+=λλλλλλa BQ a AQ a PB a AP . 由相交弦定理及勾股定理知 ,1,1222222222 -=+=-=?=λλλa BC AB AC a BQ PB BC 于是,1,122-=-=λλλa AC a BC .λ=BC AC 而C Q P ,,同时在到B A ,两点距离之比等于λ的曲线(圆)上,不共线的三点所确定的圆是唯一的,因此,圆O 上任意一点到B A ,两点的距离之比恒为.λ 性质1.当1>λ时,点B 在圆O 内,点A 在圆O 外; 当10<<λ时,点A 在圆O 内,点B 在圆O 外。 性质2.因AQ AP AC ?=2 ,过AC 是圆O 的一条切线。 若已知圆O 及圆O 外一点A ,可以作出与之对应的点,B 反之亦然。 性质3.所作出的阿波罗尼斯圆的直径为122-=λλa PQ ,面积为.12 2?? ? ??-λλπa 性质4.过点A 作圆O 的切线C AC (为切点),则CQ CP ,分别为ACB ∠的内、外角平分线。 性质5.过点B 作圆O 不与CD 重合的弦,EF 则AB 平分.EAF ∠
初中几何中线段和(差)的最值问题 一、两条线段和的最小值。 基本图形解析: 一)、已知两个定点: 1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’ 是关于直线m 的对称点。 2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。 (1)两个点都在直线外侧: (2)一个点在内侧,一个点在外侧: (3)两个点都在内侧: (4)、台球两次碰壁模型 变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、 E 点,使得围成的四边形ADEB 周长最短. 变式二:已知点A 位于直线m,n 的内侧 , 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. 二)、一个动点,一个定点: (一)动点在直线上运动: 点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动 点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: 2、点与圆在直线同侧: 三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。( 原理用平移知识解) (1)点A 、B 在直线m 两侧: 过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左 平移PQ 长,即为P 点,此时P 、Q 即为所求的点。 (2)点A 、B 在直线 m 同侧: m m A m A B m n n n m n n n m m n m n m n m m m m m
阿波罗尼斯圆性质及其应用 背景展示 阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一 (人教A 版124页B 组第3题)已知点M 与两个定点O(0,0),A(3,0)点距离的比为,求点M 的轨迹方程。 (人教A 版144页B 组第2题)已知点M 与两个定点 距离的比是一个正数m,求点M 的轨迹方程,并说明轨迹是什么图形(考虑m=1和m )。 公元前3世纪,古希腊数学家阿波罗尼斯(Apollonius)在《平面轨迹》一书中,曾研究了众多的平面轨迹问题,其中有如下著名结果:到平面上两定点距离比等于定值的动点轨迹为直线或圆.(定值为1时是直线,定值不是1时为圆) 定义:一般的平面内到两顶点A ,B 距离之比为常数( )的点的轨迹为圆,此圆称为阿波罗尼斯圆 类型一:求轨迹方程 1.已知点M 与两个定点()0,0O ,()0,3A 的距离的比为21,求点M 的轨迹方程 2.已知()02>=a a AB ,()0≥=λλMB MA ,试分析M 点的轨迹 3.(2006年高考四川卷第6题)已知两定点A (-2,0),B (1,0),如果动点P 满足条件 ,则点P 的轨迹所包围的图形面积等于( ) A . B. C. D.9 类型二:求三角形面积的最值 4.(2008江苏卷)满足条件AB = 2,AC = BC 的?ABC 的面积的最大值是 5.(2011浙江温州高三模拟)在等腰 ABC 中,AB=AC ,D 为AC 的中点,BD=3,则 ABC 面积的最大值为 6.在ABC 中,AC=2,AB=mBC(m>1),恰好当B=时 ABC 面积的最大,m=
高考数学文化内容预测三:阿波罗尼斯圆问题 一、高考考试大纲数学大纲分析及意义: 普通高考考试大纲数学修订,加强了对数学文化的考查。针对这一修订提出以下建议: 建议教师对数学文化这一概念认真学习,结合教材内容学习,特别是教材中渗透数学文化的内容要充分重视,重点研究;结合近年新课标试题中出现的与数学文化有关的试题进行学习,重点关注题源、考法命题形式。 其主要意义为: (1)增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用. (2)能力要求:经命题专家精细加工,再渗透现代数学思想和方法;在内涵方面,增加了基础性、综合性、应用性、创新性的要求. 二、往年新课标高考实例解析及2017年高考数学文化试题预测: 往年新课标高考实例分析: 分析一:古代数学书籍《九章算术》、《数书九章》等为背景 近年来在全国高考数学试题中,从《九章算术》中选取与当今高中数学教学相映的题材背景. (1)2015年高考全国卷Ⅰ,此题源于《九章算术》卷第五《商功》之[二五],将古代文化“依垣”和现代教育元素“圆锥”结合. (2)2015年高考全国卷Ⅱ,此题源于《九章算术》卷第一《方田》之[六]:“又有九十一分之四十九.问约之得几何?”“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之”,后人称之为“更相减损术”. (3)2015年高考湖北卷,此题背景源于《九章算术》卷第五《商功》之[一五].今有阳马,广五尺,袤七尺,高八尺.问积几何;之[一六]今有鳖臑,下广五尺,无袤;上袤四尺,无广,高七尺.问积几何.考题将“阳马”,“鳖臑”相结合,以《选修2-1》P109例4为源进行有机整合.巧妙嫁接,精典设问,和谐优美的考题呼之即出. 分析二:课后阅读或课后习题如阿波罗尼圆为背景 从2005-2013年多次涉及考题,全国卷2011年16题以此为命题背景的其他省市:江苏:2008年13题、2013年17题.2009-2013年湖北高考连续出现等等. 数学文化题型背景预测: 预测1:古代数学书籍《九章算术》、《数书九章》等数为背景的数学文化类题目. 预测2:高等数学衔接知识类题目.如微积分、初等数学和高等数学的桥梁,由高中向大学的知识过渡衔接. 预测3:课本阅读和课后习题的数学文化类题目.如必修3中,辗转相除法、更相减损术、秦九韶算法、二进制、割圆术等。 预测4:中外一些经典的数学问题类题目.如:回文数、匹克定理、角谷猜想、哥尼斯堡七桥问题、四色猜想等经典数学小问题值得注意。
专题一.线段和(差)的最值问题 【知识依据】 1.线段公理——两点之间,线段最短; 2.对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线; 3.三角形两边之和大于第三边; 4.三角形两边之差小于第三边; 5、垂直线段最短。 一、已知两个定点: 1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’ 是关于直线m 的对称点。 2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。 (1)两个点都在直线外侧: P m A B m A B m A B P m A B A' n m A B Q P n m A B P'Q'
(2)一个点在内侧,一个点在外侧: (3)两个点都在内侧: (4)、台球两次碰壁模型 变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短. 变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. n m A B Q P n m A B B'Q P n m A B B'A' n m A B m n A B E D m n A B A'B'm n A P Q m n A A'
二、一个动点,一个定点: (一)动点在直线上运动: 点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动:点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: 2、点与圆在直线同侧: m n A P m n A B m n A P m n A A'B m O A P'P m O B A B' m O A P m O A B A'
阿波罗尼斯圆性质及其应用探究 背景展示 阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线论》一书,阿波罗尼斯圆是他的研究成果之一。 1.“阿波罗尼斯圆”:在平面上给定两点B A ,,设P 点在同一平面上且满足 ,λ=PB PA 当0>λ且1≠λ时,P 点的轨迹是个圆,称之为阿波罗尼斯圆。 (1=λ时P 点的轨迹是线段AB 的中垂线) 2.阿波罗尼斯圆的证明. . 角坐标系中点为原点建立平面直轴,所在的直线为证明:以AB x AB ()()(), 不妨设y x P a B a A ,,0,,0,-()()22 222222,,,,PA PA PB PA PB x a y x a y PB λλλ??=∴==∴++=-+??Q ()( )()() 0112112222222=-++--+-∴a ax y x λλλλ ( ) () 2 22 2 222222 221211,01112??? ??-=+??? ? ??-+-∴=-+-+-+∴λλλλλλλa y a x a ax y x λλλλλ=??? ??-=+???? ? ?-+-∴PB PA a y a x 的解都满足又以上过程均可逆,2 22 2 221211 .120,11222为半径的圆上运动为圆心,以在以综上,动点-=???? ??-+λλλλa r a C P 3.阿波罗尼斯圆的性质. 性质1 点A 、点B 在圆心C 的同侧; 当1>λ时,点B 在圆C 内,点A 在圆C 外; 当10<<λ时,点A 在圆C 内,点B 在圆C 外。 (). ,1 1 ,012111122222的右侧当然也在点的右侧, 在点点所示,时,如图证明:当A B C a a a a a ∴>-+∴>-=--+>λλλλλλ
定义:已知平面上两点A,B,则所有满足 PA/PB=k 且不等于 1 的点 P 的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,具体的描述:一动点P 到两定点A、B 的距离之比等于定比m:n,则 P 点的轨迹,是以定比m: n 内分和外分定线段AB 的两个分点的连线为直径的圆。该圆称为阿波罗尼斯圆,简称阿氏圆。 解题策略:利用两边成比例且夹角相等构造相似三角形(简称美人鱼相似) “阿氏圆”一般解题步骤 第一步 :连接动点至圆心0(将系数不为 1 的线段的两个端点分别与圆心相连接),则连接 0P、 OB; 第二步 :计算出所连接的这两条线段OP、 OB 长度 ; 第三步 :计算这两条线段长度的比=k; 第四步 :在 0B 上取点 C,使得; 第五步 :连接 AC,与圆 0 交点即为点P. 阿氏圆最值问题例题精讲 例 1:问题提出 :如图 1,在 R△ ABC中 ,∠ ACB=90 ,CB=4,AC=6圆. C 半经为 2,P 为圆上一助点,连结 AP,BP求 AP+ BP 的最小值 尝试解决:为了解块这个间题,下面给出一种解题思路、如图2,连接 CP,在 CB 上取点D,使 CD=1 则有 ,又∵∠ PCD=∠BCP,∴△ PCD △ BCP,
∴,∴ PD=,∴ AP+AP+PD 请你完成余下的思考,并直接写出答案:AP+BP的最小值为。 自主探索 :在“间题提出”的条件不变的情况下,AP+BP的最小值为。 拓展延伸 :已知扇形COD中 ,∠ COD=90 ,0C=6,OA=3,0B=5,点 P 是弧 CD 上一点 ,求 2A+PB 的最小值。 强化训练 向内构造类型 1,如图 ,已知 AC=6,BC=8,AB=10,圆 C 的半经为4,点 D 是圆 C 上的动点 ,连接 AD、 BD, 则 AD+ BD 的最小值为。 2.在 Rt△ABC 中 ,∠ ACB=90° AC=4,BC=3,点 D 为△ ABC内一动点 ,且满足 CD=2, 则 AD+ BD 的最小值为。 3、如图 ,在 R△ ABC中 ,∠C=90° ,CA=3,CB=4⊙.C 的半径为2,点 P 是⊙ C 上一 动点 ,则 AP+ PB 的最小值为。 4、如图 ,四边形 ABCD为边长为 4 的正方形 , ⊙ B 的半径为 2,P是⊙ B 上一动点 ,则 PD+ PC的最小值为。 PD+4PC的最小值为。
直线与圆中的最值问题 一、到圆心距离的最值问题: 精品文档,超值下载 二、到圆上一点距离的最值问题: 三、与圆上一点的坐标有关的最值问题: 四、与圆半径有关的最值问题: 2213480,2210,P x y PA PB x y x y A B C PACB ++=+--+=例:已知是直线上的动点,是圆的两条切线,是切点,是圆心,求四边形面积的最小值。 2221:250P x y Q l x y PQ +=+-=例:已知是圆上一点,是直线上一点,求的最小值。 ()()()()222231,0,1,0344A B x y P PA PB P --+-=+例:已知定点和圆上的动点,求使最值时点的坐标。 ()()2204134312x x y y x x y x y ≥??≥-+-??+≤?例:设,满足求的最小值。2222,(1)1,2134 2 31x y x y y x y x y x +-=++++练习1:求实数满足求下列各式的最值:()()()()()()222430 1.2.,C x y x y C x y C P x y PM M O PM PO ++-+==练习2:已知圆:若圆的切线在轴和轴上截距相等, 求切线的方程;从圆外一点向圆引切线, 为切点,为坐标原点,且,
强化训练 1 、如图24-1,已知圆x 2+y 2=1的一条切线与x 轴、y 轴分别交于点A 、B ,则线段AB 长度的最小值为________. ()()()()()()222210,,2,2. 1.222 2..C x y x y l x y A B O OA a OB b a b C l a b AB AOB +--+===>>--=?例5:已知与曲线:相切的直线交轴,轴于两点,为原点,求证曲线与直线相切的条件是 ;求线段中点的轨迹方程; 3求的面积的最小值。 ()()()0,0, 4,0,0,3,,ABC A B C P PA PB PC ?练习3:已知三个顶点坐标,点是它的内切圆上一点,求以为直径的三个圆面积之和 的最大值和最小值。 4(1)2(2)3:1 (1)(2):20y x l x y -=练习:设圆满足: 截轴所得弦长为;被轴分成两圆弧,其弧长比为。在满足条件的所有圆中,求圆心到 直线的距离最小的圆的方程。
线段和(差)的最值问题 此类问题特点:1.两个定点,一个定点;2. 线段和最小值,线段差最大值 一、线段和最小值问题 若在一条直线m上,求一点P,使PA+PB最小; (1)两侧/异侧型:定点A、 B在直线m(动点P所在直线)两侧:直接连接A、B两点交直线m于一点P,该点P即为所求点。(PA+PB=AB) (2)同侧型:定点A、B在动点P所在直线m同侧:(方法:一找二作三连): 一找:找定点A、B,动点P及动点所在的直线m;二作:任选一个定点做对称;三连:连接对称点与另一个定点,其连线交动点所在直线于一点P,该点P即为所求。(PA+PB=PA’+PB=A’B) m A B P m A B 二、线段差最大值问题 若在一条直线m上,求一点P,使得最大 (1)同侧型:定点A、B在直线m(动点P所在直线)两侧:直接连接A、B两点交直线m于一点P,该点P即为所求点。() (2)两侧/异侧型:定点A、B在直线m(动点P所在直线)两侧:任选一个定点做对称;三连:连接对称点与另一个定点,其连线交动点所在直线m于一点P,该点P即为所求点。()
线段和最小值练习题 1.如图1,在锐角三角形ABC中,AB=,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值为. 2. 如图2所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为. 3.如图3,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为__________. 图1 图2 图3 图4 4. 如图4,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为. 5. 如图5,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm. 6.已知正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB +PE的最小值是 7. 如图6,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为. 8.如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ 周长的最小值为cm.(结果不取近似值) 图5 图6 图7 9. 如图8,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是.
“阿波罗尼斯圆”的应用举例 【例】 阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果击中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一,指的是:已知动点M 与两定点A 、B 的距离之比为 λ(0λ>, 1λ≠) ,那么点M 的轨迹就是阿波罗尼斯圆.下面,我们来研究与此相关的一个问题.已知圆: 221x y +=和点1,02A ??- ??? ,点()1,1B , M 为圆O 上动点,则2MA MB +的最小值为( ) A. 6 B. 7 C. 10 D. 11答案 C 解析 令2=MA MC ,则12 MA MC =. 由题意可得圆221x y +=是关于点A,C 的阿波罗尼斯圆,且1=2 λ。 设点C 坐标为(),C m n , 则()()2 2221212 x y MA MC x m y n ??++ ???==-+-。 整理得2222 2421333m n m n x y x y ++-+++=。
由题意得该圆的方程为221x y +=, ∴2224020113m n m n +==+-????? =???? ,解得2{ 0m n =-=。 ∴点C 的坐标为(-2,0)。 ∴2MA MB MC MB +=+, 因此当点M 位于图中的12,M M 的位置时, 2MA MB MC MB +=+的值最小,且为10,故选C. 【练习】 1.设椭圆与双曲线有共同的焦点F 1(-1,0),F 2(1,0),且椭圆长轴是双曲线实轴的2倍,则椭圆与双曲线的交点轨迹是( ) A .双曲线 B .一个圆
圆锥曲线专题突破一:与直线和圆有关的最值问题 题型一 有关定直线、定圆的最值问题 例1 已知x ,y 满足x +2y -5=0,则(x -1)2 +(y -1)2 的最小值为________. 破题切入点 直接用几何意义——距离的平方来解决,另外还可以将x +2y -5=0改写成x =5-2y ,利用二次函数法来解决. 解析 方法一 (x -1)2+(y -1)2 表示点P (x ,y )到点Q (1,1)的距离的平方. 由已知可知点P 在直线l :x +2y -5=0上,所以PQ 的最小值为点Q 到直线l 的距离, 即d =|1+2×1-5|1+22 =255,所以(x -1)2+(y -1)2的最小值为d 2 =45. 方法二 由x +2y -5=0,得x =5-2y ,代入(x -1)2 +(y -1)2 并整理可得 (5-2y -1)2+(y -1)2=4(y -2)2+(y -1)2=5y 2 -18y +17=5(y -95)2+45,所以可得最小值为45. 题型二 有关动点、动直线、动圆的最值问题 例2 直线l 过点P (1,4),分别交x 轴的正方向和y 轴的正方向于A 、B 两点.当OA +OB 最小时,O 为坐标原点,求l 的方程. 破题切入点 设出直线方程,将OA +OB 表示出来,利用基本不等式求最值. 解 依题意,l 的斜率存在,且斜率为负,设直线l 的斜率为k ,则y -4=k (x -1)(k <0). 令y =0,可得A (1-4 k ,0);令x =0,可得B (0,4-k ). OA +OB =(1-4k )+(4-k )=5-(k +4k )=5+(-k +4 -k )≥5+4=9. 所以,当且仅当-k =4 -k 且k <0,即k =-2时,OA +OB 取最小值.这时l 的方程为2x +y -6=0. 题型三 综合性问题 (1)圆中有关元素的最值问题 例3 由直线y =x +2上的点P 向圆C :(x -4)2 +(y +2)2 =1引切线PT (T 为切点),当PT 的长最小时,点P 的坐标是________. 破题切入点 将PT 的长表示出来,结合圆的几何性质进行转化. 解析 根据切线段长、圆的半径和圆心到点P 的距离的关系,可知PT =PC 2 -1,故PT 最小时,即PC 最小,此时PC 垂直于直线y =x +2,则直线PC 的方程为y +2=-(x -4),即y =-x +2,联立方程? ?? ?? y =x +2, y =-x +2,解得点P 的坐标 为(0,2). (2)与其他知识相结合的范围问题 例4 已知直线x +y -k =0(k >0)与圆x 2+y 2 =4交于不同的两点A ,B ,O 是坐标原点,且有|OA →+OB →|≥33 |AB →|,那么 k 的取值范围是________. 破题切入点 结合图形分类讨论.
求线段和(差)的最值问题 【知识依据】:1.线段公理——两点之间,线段最短;2.对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;3.三角形两边之和大于第三边;4.三角形两边之差小于第三边。5、垂直线段最短 一、已知两个定点: 1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’ 是关于直线m 的对称点。 2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。 (1)两个点都在直线外侧: m m A B m A B m n m n
(2)一个点在内侧,一个点在外侧: (3)两个点都在内侧: (4)、台球两次碰壁模型 变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短. 变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. n m A n n n m
二、一个动点,一个定点: (一)动点在直线上运动: 点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动 点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: 2、点与圆在直线同侧: m n m n m n m m m m m
从课本中的阿波罗尼斯圆问题 探讨数学文化在教学中的渗透 靖江市第一高级中学 数学组 印栋 E-mail: yde2003@https://www.doczj.com/doc/6316157345.html, 邮编:214500 克莱因在其名著《西方文化中的数学》中指出:数学是一种精神,一种理性的精神.正是这种精神,激发、促进、鼓舞并驱使人类的思维得以运用到最完善的程度,亦正是这种精神,试图决定性地影响人类的物质、道德和社会生活;试图回答有关人类自身存在提出的问题;努力去理解和控制自然;尽力去探求和确立已经获得知识的最深刻的和最完美的内涵.因此,美国数学学会主席魏尔德说:“数学是一种会不断进化的文化”.正是数学与文化以及数学文化的不断交融及相互促进,才使数学在人类文明的发展中起到了举足轻重的作用并获得了如此多的赞誉.在新课程改革中,数学文化不再是被孤立的装饰品,而是渗透在相关模块和专题中. 新课标《苏教版·必修2》在第2章平面解析几何初步第2.2节圆与方程介绍了圆的标准方程和一般方程后编排了这样一道习题: 习题2.2(1)10.已知点)(y x M ,与两个定点)03()00(,,, A O 的距离之比为2/1,那么点M 的坐标应满足什么关系?画出满足条件的点M 所形成的曲线. 分析:由于有了课上推导圆标准方程的过程可作为参照,大部分学生不需费太多的气力就可以解出上述的问题,解法如下. 解析:由题知2/1/=MA MO ,将距离公式代入可得 12 =, 化简整理即得到该曲线的方程为: 4)1(22=++y x . 因此,所求点M 所形成的曲线是以(-1,0)为圆心,2为半径的圆(图略). 这道题实际上源自约公元前262~前190的古希腊人阿波罗尼斯(Apollonius of Perga ,也有文献上将其名字翻译为“阿波罗尼奥斯”)在其巨著《圆锥曲线论》给出的一个著名的几何问题:“在平面上给定两点A 、B ,设P 点在同一平面上且满足λ=PB PA /,当λ大于0且λ≠1时,P 点的轨迹是个圆”,这个圆我们称之为“阿波罗尼斯圆”,这个结论称作“阿波罗尼斯轨迹”. 同上题一样,我们用解析法完全可以证明:与A 、B 距离之比等于λ的动点轨迹为圆.但如果每题都先用解析法求出圆的方程,再根据圆心及半径作出圆,显然很费事,特别是对一些选择题或填空题如此解法实在小题大做,能 否找出阿 波罗尼斯圆的简捷作法?下述定理可给出明 确答案. 定理:A 、B 为两已知点,P 、Q 分别为 线段A B 的定比为λ(λ≠1)的内、外分点,则以P 、Q 为直径的
二次函数之最值问题 ◆ 线段和或差(或三角形周长)最值问题:此类问题一般是利用轴对称的性质和两点之间线段最短确定最 短距离,这个距离一般用勾股定理或两点之间距离公式求解.特殊地,也可以利用平移和轴对称的知识求解固定线段长问题. ◆ 最短距离和找法:以动点所在的直线为对称轴,作一个已知点的对称点,连结另一个已知点和对称点的 线段,与对称轴交于一点,这一点即为所求点.线段长即为最短距离和. ◆ 线段长最值问题:根据两点间距离公式12x x -把线段长用二次函数关系式表示出来求最值. 几何面积最值问题:此类问题一般是先运用三角形相似,对应线段成比例等性质或者用“割补法”或者利用平行线得到三角形同底等高进行面积转化写出图形的面积y与边长x 之间的二次函数关系,其顶点的纵坐 标即为面积最值. 例1、已知二次函数2y x bx c =++的图象过点()3,0A -和点()1,0B ,且与y 轴交于点C ,D 点在抛物线上且横坐标是2-.(1)求抛物线的解析式;(2)抛物线的对称轴上有一动点P,求出PA PD +的最小值.? ? ?例2、如图,在平面直角坐标系xOy 中,直线3 2y x =- +分别交x轴、y 轴于C 、A 两点.将射线AM 绕着点A顺时针旋转45°得到射线AN.点D 为AM上的动点,点B 为AN 上的动点,点C 在∠MAN 的内部. (1)求线段A C的长; (2)求△BC D周长的最小值; (3)当△BCD 的周长取得最小值,且52 BD =时,△BCD 的面积为________. ? ?????1、已知抛物线21y ax bx =++经过点()1,3A 和点()2,1B .(1)求此抛物线解析式; (2)点C、D 分别是x轴和y 轴上的动点,求四边形ABCD 周长的最小值;?(3)过点B作x 轴的垂线,垂足为E 点.点P 从抛物线的顶点出发,先沿抛物线的对称轴到达F 点,再沿FE 到达E 点,若P 点在对称轴上的运动速度是它在直线FE 上运动速度的2倍,试确定点F 的位置,使 得点P 按照上述要求到达E 点所用的时间最短.????
阿波罗尼斯圆性质及其应用 背景展示 阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一 (人教A版124页B组第3题)已知点M与两个定点O(0,0),A(3,0)点距离的比为,求点M的轨迹方程。 (人教A版144页B组第2题)已知点M与两个定点距离的比是一个正数m,求点M的轨迹方程,并说明轨迹是什么图形(考虑m=1和m)。 公元前3世纪,古希腊数学家阿波罗尼斯(Apollonius)在《平面轨迹》一书中,曾研究了众多的平面轨迹问题,其中有如下著名结果:到平面上两定点距离比等于定值的动点轨迹为直线或圆.(定值为1时是直线,定值不是1时为圆) 定义:一般的平面内到两顶点A,B距离之比为常数()的点的轨迹为圆,此圆称为阿波罗尼斯圆
类型一:求轨迹方程 1.已知点M 与两个定点()0,0O ,()0,3A 的距离的比为2 1 ,求点M 的轨迹方程 2.已知()02>=a a AB ,()0≥=λλMB MA ,试分析M 点的轨迹 3.(2006年高考四川卷第6题)已知两定点A (-2,0),B (1,0),如果动点P 满足条件,则点P 的轨迹所包围的图形面积等于( ) A . B. C. D.9 类型二:求三角形面积的最值 4.(2008江苏卷)满足条件AB = 2,AC = BC 的?ABC 的面积的最大值是 5.(2011浙江温州高三模拟)在等腰ABC 中,AB=AC ,D 为AC 的中点,BD= 3,则ABC 面积的最大值为 6.在ABC 中,AC=2,AB=mBC(m>1),恰好当B=时 ABC 面积的最大,m= 类型三:定点定值问题
阿氏圆题型的解题方法和技巧对于此类问以阿氏圆(阿波罗尼斯圆)为背景的几何问题近年来在中考数学中经常出现,. 题的归纳和剖析显得非常重要具体内容如下:的距离P到两定点A、B(阿氏圆定理全称:阿波罗尼斯圆定理),具体的描述:一动点mm nn的两个分点的连内分和外分定线段是以定比之比等于定比≠(1),则P点的轨迹,AB简线为直径的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现,该圆称为阿波罗尼斯圆,称阿氏圆.1)P≠,(k定理读起来和理解起来比较枯燥,阿氏圆题型也就是大家经常见到的PA+kPB. 点的运动轨迹是圆或者圆弧的题型 PA+kPB,(k≠1)P点的运动轨迹是圆或圆弧的题型 母子三角形相似阿氏圆基本解法:构造是平面n).点PC(m,0),D(0,轴分别有点问题【】在平面直角坐标系xOy中,在x轴、y. ,求PC+kPD的最小值内一动点,且OP=r 阿氏圆一般解题步骤:若圆已经画出则可省为半径画圆;(,以点O为圆心、r)第一步:确定动点的运动轨迹(圆) 略这一步 OD;即连接OP、的线段的固定端点与圆心相连接第二步:连接动点至圆心O(将系数不为1),长度;OP、OD第三步:计算出所连接的这两条线段;第四步:计算这两条线段长度的比k OM:OP=OP:OD=k,使得;第五步:在OD上取点M. 即所求的最小值P交点即为点.此时CMCM第六步:连接,与圆O提到先把k直接计算,【补充:若能直接构造△相似计算的,不能直接构造△相似计算的,1,再构造△相似进行计算】括号外边,将其中一条线段的系数化成k 1 习题的中点,将线段为BDACB=90°,D为AC的中点,MRt【旋转隐圆】如图,在△ABC中,∠,那么在旋转,BC=3点任意旋转(旋转过程中始终保持点M为BD的中点),若AC=4AAD绕 ___________. CM长度的取值范围是过程中,线段2BD为△ABC内一动点,满足CD=2,则AD+ABC1.Rt△中,∠ACB=90°,AC=4,BC=3,点D3_______. 的最小值为上任取一,在⊙A与°,⊙ABC相切于点E2.如图,菱形ABCD的边长为2,锐角大小为603________. 的最小值为点P,则PDPB+2
直线与圆位置关系 一.课标要求 1.能根据给定直线、圆的方程,判断直线与圆的位置关系; 2.能用直线和圆的方程解决一些简单的问题; 3.在平面解析几何初步的学习过程中,体会用代数方法处理几何问题的思想。 二.知识框架 相离 几何法 弦长 直线与圆的位置关系 相交 代数法 切割线定理 相切 直线与圆 代数法 求切线的方法 几何法 圆的切线方程 过圆上一点的切线方程 圆的切线方程 切点弦 过圆外一点的切线方程 方程 三.直线与圆的位置关系及其判定方法 1.利用圆心0),(=++C By Ax b a O 到直线的距离2 2 B A C Bb Aa d +++=与半径r 的大小来判 定。 (1)?
(位置关系)1.已知动直线5:+=kx y l 和圆1)1(:2 2=+-y x C ,试问k 为何值时,直线与圆相切、相离、相交? (位置关系)2.已知点),(b a M 在圆1:2 2 =+y x O 外,则直线1=+by ax 与圆O 的位置关系是() A.相切 B.相交 C.相离 D.不确定 (最值问题)3.已知实数x 、y 满足方程0142 2 =+-+x y x , (1)求 x y 的最大值和最小值; (2)求y x -的最大值和最小值; (3)求2 2 y x +的最大值和最小值。 〖分析〗考查与圆有关的最值问题,解题的关键是依据题目条件将其转化为对应的几何问题求解,运用数形结合的方法,直观的理解。①转化为求斜率的最值;②转化为求直线b x y +=截距的最大值;③转化为求与原点的距离的最值问题。 (位置关系)4.设R n m ∈,,若直线02)1()1(=-+++y n x m 与圆1)1()1(2 2 =-+-y x 相切,则n m +的取值围是() (位置关系)5.在平面直角坐标系xoy 中,已知圆224x y +=上有且仅有四个点到直线 1250x y c -+=的距离为1,则实数c 的取值围是 6.直线0323=-+y x 截圆x 2+y 2=4得的劣弧所对的圆心角是 ( C ) A 、 6π B 、4π C 、3π D 、2 π (位置关系)7.圆01222 2 =+--+y x y x 上的点到直线2=-y x 的距离最大值是( ) A .2 B .21+ C .2 2 1+ D .221+ (最值问题)8.设A 为圆1)2()2(22=-+-y x 上一动点,则A 到直线05=--y x 的最大距离为______. 9.已知圆C 的半径为2,圆心在x 轴的正半轴上,直线0443=++y x 与圆C 相切,则圆 C 的方程为( ) A .0322 2 =--+x y x B .042 2=++x y x C .0322 2 =-++x y x D .042 2 =-+x y x
求线段(或线段和)(周长)最值问题 福建莆田月塘中学潘立城 中考数学压轴题中常出现有关几何最值问题,很多同学不知如何想,无从下手,感到这类题目很难,应该是尖子生同学做的题目,与我们这些一般生无关,避而远之。 这类题目很多,内容丰富,涉及面广,解法灵活多样,就像孙悟空七十二变,变化多端。孙悟空再怎么变化,也跑不出如来佛的“手掌心”。 解几何最值的“手掌心”是什么呢? : 撑握了如来佛的这一法宝,有关几何最值的各种“妖魔鬼怪”题都能解答。 一、“手掌心”法宝: 三角形中两边之和大于第三边 特征:“一”条线段且“动”点“不”在定线上,无规律找关键点:定点,中点,圆心。 ④线段的转移 特征:“定”点在“定”直线上 ⑤二次函数最值 特征:有“表达式” ①垂线段最短 ②两点间线段最短 “弯”线 变 “直”线 特征 “直”线的特征 ①“直”线:定点--动点 (定点--动点--动点) (动点--动点--动点) ②直:定点--动点--定点 直:动点--定点--动点
二、类型名词解释:定直线指动点运动所在的直线 ①垂线段最短特征:“弯”线变“直 ”线对称轴 l A C B M 定点 “弯”线 “直”线 例2.(2012湖北鄂州3分)在锐角三角形ABC中, BC=2 4,∠ABC=45°,BD平分∠ABC,M、N分 别是BD、BC上的动点,则CM+MN的最小值是 4 。 ①标:定点A,定点C,动点B 定直线AC,定直线l ②特征:“弯”线变“直”线 对称轴:定直线l 作点A关于定直线l的对称点M “弯”线AB+BC变“直”线MC “直”线:定点M--动点B--定点C 垂线段最短 ①标:定点C,动点M,动点N 定直线BD,定直线BC ②特征:“弯”线变“直”线 对称轴:定直线BD 作点N关于定直线BD的对称点E “弯”线CM+MN变“直”线CME “直”线:定点C--动点M--动点E 垂线段最短
2020中考数学线段最值问题之阿波罗尼斯圆(阿氏圆) 【知识背景】 阿波罗尼斯与阿基米德、欧几里德齐名,被称为亚历山大时期数学三巨匠。阿波罗尼斯对圆锥曲线有深刻而系统的研究,其主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是其研究成果之一,本文主要讲述阿波罗尼斯圆在线段最值中的应用,下文中阿波罗尼斯圆简称为“阿氏圆”。 【定 义】 阿氏圆是指:平面上的一个动点P 到两个定点A ,B 的距离的比值等于k ,且k≠1的点P 的轨迹称之为阿氏圆。即: )1(≠=k k PB PA ,如下图所示: 上图为用几何画板画出的动点P 的轨迹,分别是由图中红色和蓝色两部分组成的的圆,由于是静态文档的形式,无法展示动图,有兴趣的可以用几何画板试一试。 【几何证明】 证明方法一:初中纯几何知识证明:阿氏圆在高中数学阶段可以建立直角坐标系,用解析几何的方式来确定其方程。但在初中阶段,限于知识的局限性,我们可以采用纯几何的证明方式,在证明前需要先明白角平分线定理及其逆定理,请看下文: 知识点1:内角平分线定理及逆定理
若AD 是∠BAC 的角平分线,则有: CD BD AC AB = 。即“两腰之比”等于“两底边之比”。 其逆定理也成立:即CD BD AC AB = ,则有:AD 是∠BAC 的角平分线。 知识点2:外角平分线定理及其逆定理 若AD 是△ABC 外角∠EAC 的角平分线,则有 CD BD AC AB = 。即“两腰之比”等于“两底边之比”。 其逆定理也成立:即CD BD AC AB = ,则有:AD 是外角∠EAC 的角平分线。 【阿氏圆的证明】 有了上述两个知识储备后,我们开始着手证明阿氏圆。