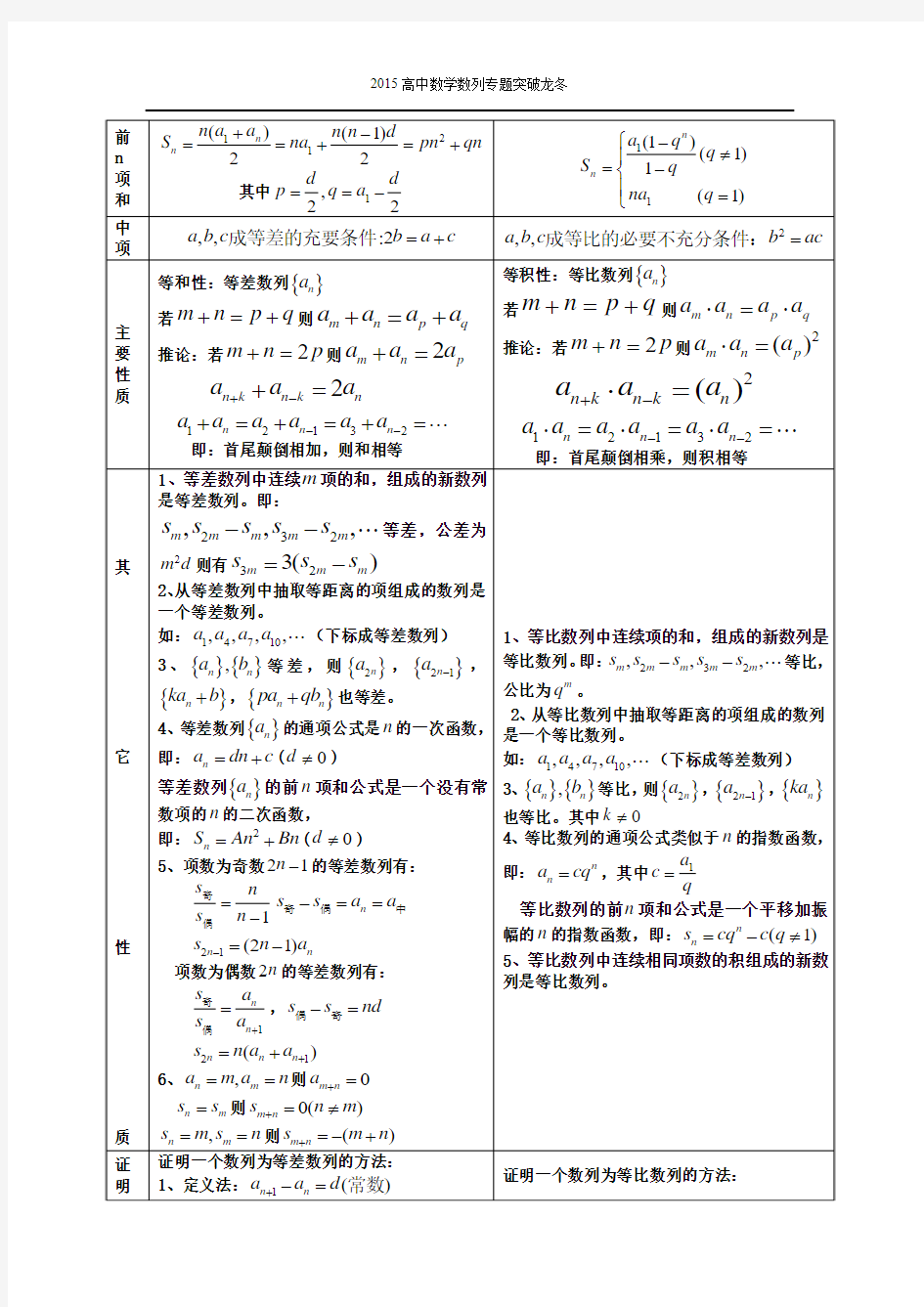
当前位置：文档之家› 2015新课标高中数学--数列专题突破-老师版----一轮二轮复习资料

2015新课标高中数学--数列专题突破-老师版----一轮二轮复习资料

数列

数列的概念和表示法

（1）数列定义：按一定次序排列的一列数叫做数列；数列中的每个数都叫这个数列的项记作n a ，在数列第一个位置的项叫第1项（或首项），在第二个位置的叫第2项，……，序号为n 的项叫第n 项（也叫通项）记作n a ；

数列的一般形式：1a ，2a ，3a ，……，n a ，……，简记作{}n a 。

（2）通项公式的定义：如果数列}{n a 的第n 项与n 之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式

说明：①{}n a 表示数列，n a 表示数列中的第n 项，n a = ()f n 表示数列的通项公式；

②同一个数列的通项公式的形式不一定唯一。

③不是每个数列都有通项公式。例如，1，1.4，1.41，1.414，…… （3）数列的函数特征与图象表示：序号：1 2 3 4 5 6 项：4 5 6 7 8 9

上面每一项序号与这一项的对应关系可看成是一个序号集合到另一个数集的映射。从函数观点看，数列实质上是定义域为正整数集N +（或它的有限子集）的函数()f n 当自变量n 从1开始依次取值时对应的一系列函数值(1),(2),(3),f f f ……，

()f n ，……．通常用n a 来代替()f n ，其图象是一群孤立的点

（4）数列分类：

①按数列项数是有限还是无限分：有穷数列和无穷数列；

②按数列项与项之间的大小关系分：单调数列（递增数列、递减数列）、常数列和摆动数列

（5）递推公式定义：

如果已知数列{}n a 的第1项（或前几项），且任一项n a 与它的前一项1n a -（或前几项）间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的递推公式

通项公式a n 与求和公式S n 的关系可表示为：11(1)

(n 2)

n n n S n a S S -=?=?-≥?

数列的项

a与前n项和

S的关系：1

(1)

(2)

n n

s n

s s n

-≥

数列求和的常用方法：

1、拆项分组法：即把每一项拆成几项，重新组合分成几组，转化为特殊数列求和。

2、错项相减法：适用于差比数列（如果{}n a等差，{}n b等比，那么{}

n n

a b叫做差比

数列）

即把每一项都乘以{}n b的公比q，向后错一项，再对应同次项相减，

转化为等比数列求和。

3、裂项相消法：即把每一项都拆成正负两项，使其正负抵消，只余有限几项，可求和。

适用于数列

n n

a a

和

（其中{}n a等差）

可裂项为：

1111

()

n n n n

a a d a a

等差数列前n项和的最值问题：

1、若等差数列{}n a的首项10

a>，公差0

d<，则前n项和

S有最大值。

（ⅰ）若已知通项

a，则

S最大?

≥

≤

；

（ⅱ）若已知2

S pn qn

=+，则当n取最靠近

-的非零自然数时

S最大；

2、若等差数列{}n a的首项10

a<，公差0

d>，则前n项和

S有最小值

（ⅰ）若已知通项

a，则

S最小?

≤

≥

；

（ⅱ）若已知2

S pn qn

=+，则当n取最靠近

-的非零自然数时

S最小；

数列通项的求法：

⑴公式法：①等差数列通项公式；②等比数列通项公式。

⑵已知

S（即

()

a a a f n

+++=

）求

a，用作差法：{11,(1),(2)

n n

S n

a S S n

=-≥。

已知12()n a a a f n = 求n a ，用作商法：(1),(1)()

,(2)

(1)

n f n f n a n f n =??=?

≥?-?。 ⑶已知条件中既有n S 还有n a ，有时先求n S ，再求n a ；有时也可直接求n a 。

⑷若1()n n a a f n +-=求n a 用累加法：11221()()()n n n n n a a a a a a a ---=-+-++- 1a +(2)n ≥。

⑸已知1()n n a f n a +=求n a ，用累乘法：121121

n n n n n a a a

a a a a a ---=???? (2)n ≥。

⑹已知递推关系求n a ，用构造法（构造等差、等比数列）。

特别地，（1）形如1n n a ka b -=+、1n n n a ka b -=+（,k b 为常数）的递推数列都可以用待定系数法转化为公比为k 的等比数列后，再求n a ；形如1n n n a ka k -=+的递推数列都可以除以n

k 得到一个等差数列后，再求n a 。

（2）形如1

1n n n a a ka b

--=

+的递推数列都可以用倒数法求通项。

（3）形如1k n n a a +=的递推数列都可以用对数法求通项。

（7）数学归纳法。（8）当遇到q a a d a a n n n n ==--+-+1

11或

时，分奇数项偶数项讨论，结果可能是分段形式。数列求和的常用方法：

（1）公式法：①等差数列求和公式；②等比数列求和公式。

（2）分组求和法：在直接运用公式法求和有困难时，常将“和式”中“同类项”先合并在一起，再运用公式法求和。

（3）倒序相加法：若和式中到首尾距离相等的两项和有其共性或数列的通项与组合数相关联，则常可考虑选用倒序相加法，发挥其共性的作用求和（这也是等差数列前n 和公式的推导方法）.

（4）错位相减法：如果数列的通项是由一个等差数列的通项与一个等比数列的通项相乘构成，那么常选用错位相减法（这也是等比数列前n 和公式的推导方法）.

（5）裂项相消法：如果数列的通项可“分裂成两项差”的形式，且相邻项分裂后相关联，那么常选用裂项相消法求和.常用裂项形式有：

①

111(1)1n n n n =-++； ②1111()()n n k k n n k =-++； ③2211111()1211k k k k <=---+，21111111

1(1)(1)1k k k k k k k k k

-=<<=-++--；

④1111[](1)(2)2(1)(1)(2)n n n n n n n =-+++++ ；⑤11

(1)!!(1)!

n n n n =-

++；

⑥=

<<= 二、解题方法：

求数列通项公式的常用方法： 1、公式法

2、n n a S 求由：1

(1)(2)n n n s n a s s n -=?=?-≥?

3、求差（商）法

{}如：满足……a a a a n n n n 12121

225

1122+++=+<>

解：n a a ==?+=11

22151411时，，∴

n a a a n n n ≥+++=-+<>--212121

215

212211时，……

<>-<>=121

2得：n n a

∴a n n =+21

∴a n n n n ==≥???+1412

()

() ［练习］

{}数列满足，，求a S S a a a n n n n n +=

=++1115

4 （注意到代入得：a S S S

S n n n n n

+++=-=1

114

{}又，∴是等比数列，S S S n n n 144==

n a S S n n n n ≥=-==--23411时，……·

4、叠乘法

{}例如：数列中，，

，求a a a a n

n a n n n n 1131

==++ 解：

a a a a a a n n a a n

n n n 21321

1122311

·……·……，∴-=-= 又，∴a a n

n 133

5、等差型递推公式

由，，求，用迭加法a a f n a a a n n n -==-110()

n a a f a a f a a f n n n ≥-=-=-=???

??-22321321时，…………两边相加，得：()()()

a a f f f n n -=+++123()()()……

∴……a a f f f n n =++++023()()()

［练习］

{}()数列，，，求a a a a n a n n n n n 111132==+≥--

()

（）a n n =-1

6、等比型递推公式（待定系数法）

()

a ca d c d c c d n n =+≠≠≠-1010、为常数，，，

()可转化为等比数列，设a x c a x n n +=+-1 ()?=+--a ca c x n n 11

令，∴()c x d x d c -==

-11

∴是首项为，为公比的等比数列a d c a d c c n +-?

???+

-111 ∴·a d c a d c c n n +-=+-?? ??

?-1111

∴a a d c c d c n n =+-?

? ???-

--1111

［练习］

{}数列满足，，求a a a a a n n n n 11934=+=+

（）a n n =-?? ?

+-84311

7、倒数法

例如：，，求a a a a a n n

n n 11122

由已知得：1

221211a a a a n n n n

+=+=+

∴11121a a n n +-= ∴??????

=111121a a n 为等差数列，，公差为

()()∴=+-=+1111212

1a n n n · ∴a n n =

数列前n 项和的常用方法：

1、公式法：等差、等比前n 项和公式

2、裂项法：把数列各项拆成两项或多项之和，使之出现成对互为相反数的项。

{}如：是公差为的等差数列，求a d a a n k k k n

1+=∑

解：()()由

·11111011a a a a d d a a d k k k k k k ++=+=-?? ?

?≠

∴11111111a a d a a k k k n

k k k n

+=+=∑∑=-?? ?

=-?? ???+-?? ???++-?? ??????

???=

-?? ??

?++11111111111223111d a a a a a a d a a n n n ……

［练习］

求和：…………111211231123+

++++++++++n

（…………，）a S n n n ===-

+21

3、错位相减法：

{}{}{}若为等差数列，为等比数列，求数列（差比数列）前项a b a b n n n n n

{}和，可由求，其中为的公比。S qS S q b n n n n -

如：……S x x x nx n n =+++++<>-12341231 ()x S x x x x n x nx n n n

·……=+++++-+<>-234122341

()<>-<>-=++++--121121：……x S x x x nx n n n

()()

x S x x nx x

≠=---

-11112

时，

()x S n n n n ==++++=

+112312

时，……

4、倒序相加法：把数列的各项顺序倒写，再与原来顺序的数列相加。

S a a a a S a a a a n n n n n n =++++=++++???

?--121121…………相加

()()()21211S a a a a a a n n n n =++++++-…………

［练习］

已知，则f x x x f f f f f f f ()()()()()=+++?? ???++?? ???++?? ?

??=22

11212313414

（由f x f x x x x x x x x ()+?? ?

??=++

?? ??

?+?? ?

?=+++=1111111112

2222 ∴原式=++?? ?????

????++?? ?????????++?? ???????

??f f f f f f f ()()()()1212313414

=+++=12111312

）高考练习

1. 等比数列{}n a 的各项均为正数，且212326231,9.a a a a a +== （1）.求数列{}n a 的通项公式.

（2）.设31323log log ......log ,n n b a a a =+++求数列1n b ??

???

的前项和. 解：（Ⅰ）设数列{a n }的公比为q ，由23269a a a =得32

9a a = 所以2

19q =

。有条件可知a>0,故13

q =。由12231a a +=得12231a a q +=，所以113

a =

。故数列{a n }的通项式为a n =1

3n 。

（Ⅱ）111111log log ...log n b a a a =+++

(12...)

(1)

2n n n =-++++=-

故12112()(1)1n b n n n n =-=--++ 12111111112...2((1)()...())22311

n n

b b b n n n +++=--+-++-=-

++ 所以数列1

{}n

b 的前n 项和为21n n -+

2. 已知等差数列{an}满足a2=0，a6+a8=-10

（I ）求数列{an}的通项公式；

（II ）求数列的前n 项和．

解：（I ）设等差数列的公差为d ，由已知条件可得

解得

故数列

的通项公式为 ………………5分（II ）设数列，即，

所以，当时，

所以

综上，数列 ………………12分

3.设数列{}n a 满足21112,32n n n a a a -+=-= （1）求数列{}n a 的通项公式；（2）令n n b na =，求数列的前n 项和n S 解：（Ⅰ）由已知，当n ≥1时，

?????-12n n a {}n a 110,

21210,a d a d +=??

+=-?11,

1.a d =??

=-?{}n a 2.n a n =-1{}2n n n a n S -的前项和为2111

,122n n n a a S a S -=+++= 故12.2242n n n S a

a a =+++ 1n >121

1111222211121()

2422

121(1)22n n n n n n

n n n n

S a a a a a a n n

------=+++--=-+++--=--- .2n

n 1.

2n n n S -=11{

}.22n n n n a n

n S --=的前项和

111211[()()()]n n n n n a a a a a a a a ++-=-+-++-+

21233(222)2n n --=++++ 2(1)12n +-=。而 12,a =

所以数列{n a }的通项公式为212n n a -=。（Ⅱ）由212n n n b na n -==?知

35211222322n n S n -=?+?+?++? ①

从而23572121222322n n S n +?=?+?+?++? ② ①-②得

2352121(12)22222n n n S n -+-?=++++-? 。

即 21

1[(31)2

2]9

n n S n +=-+ 4．已知数列{a n }满足a 1=1,a 2=3,a n+2=3a n+1-2a n （n ∈N +

）（1）证明：数列{a n+1-a n }是等比数列；（2）求数列{a n }的通项公式解：（1）证明：

是以为首项，2为公比的等比数列。

（2）解：由（1）得[来源:学科网]

5．在数列{}n a 中，12a =，1431n n a a n +=-+，n ∈*

N ．（1）证明数列{}n a n -是等比数列；

（2）设数列{}n a 的前n 项和n S ，求n n S S 41-+的最大值。

解：证明：（Ⅰ）由题设1431n n a a n +=-+，得1(1)4()n n a n a n +-+=-，n ∈*

N ．又111a -=，所以数列{}n a n -是首项为1，且公比为4的等比数列．

（Ⅱ）由（Ⅰ）可知14n n a n --=，于是数列{}n a 的通项公式为14n n a n -=+．所以数列{}

n a 的前n 项和41(1)

n n n n S -+=+． 1141(1)(2)

41(1)44323

2n n n n n n n n S S ++??-++-+-=+-+ ???

= )43(2

-+-n n 故n=1，最大0.

6. 已知数列的各项满足：，.

2132,n n n a a a ++=- 21112*21

12(),1,3,2().

n n n n n n n n

a a a a a a a a n N a a ++++++∴-=-==-∴

=∈- {}1n n a a +∴-21a a -2=*

12(),

n n a a n N +-=∈112211()()...()n n n n n a a a a a a a a ---∴=-+-++-+12*

22...2121().

n n n

n N --=++++=-∈{}n a k a 311-=)(R k ∈1

143n n n a a --=-

(1) 判断数列是否成等比数列；

（2）求数列的通项公式；

解：（1），

．

当时，，则数列不是等比数列；

当时，，则数列是公比为的等比数列．

（2）由（1）可知当时，，．

当时，，也符合上式，

所以，数列的通项公式为．

7. 已知正项等差数列的前项和为，若，且成等比数列.

（Ⅰ）求的通项公式；

（Ⅱ）记的前项和为，求. 解：（Ⅰ）∵，即，∴，所以，

又∵，，成等比数列，

∴，即，解得，或（舍去），

∴，故；

（Ⅱ），设， ①

则， ② ①②得，

4{n

n a -{}n a n n n n n

n n a a a 47

33743474111?+-=--=-+++)74(3n

n a --=k k a 373

7431741-=--=-17k =0741=-a }7

4{n

n a -17k ≠0741≠-a }7

4{n

n a -3-17k ≠1)3()37

(74--?-=-

n n n k a 7

4)3()373(1

n n n k a +-?-=-17k =7

n a ={}n a 7

4)3()373(1

n n n k a +-?-=-{}n a n n S 312S =1232,,1a a a +{}n a 3

n n a b =

n n T n T 312S =12312a a a ++=2312a =24a =12a 2a 31a +2

2132(1)a a a =?+2

2222()(1)a a d a d =-?++3d =4d =-121a a d =-=32n a n =-1321123333n n n n n n

a n

b n --=

==?-?2311111

12343333

n n A n -=+?+?+?++? 234111111

234333333

n n A n =+?+?+?++? -231211111

1333333

n n n A n -=+++++-? 1113313()1322313

n n n n -=-?=-+?-

∴， ∴． 8. 已知等差数列和正项等比数列，，，＝

（1）求数列、的通项公式

（2）若，求数列的前项和. 解（1）依题意，为等差数列，设其公差为；为正项等比数列，设其公比为，

则可知

∵ ∴可知2,即又 ∴ ，解得故由已知＝＝4, ∴ ，即 ∴

所以，（2）∵ ＝

∴ ＝

以上两式相减，得－＝＝

＝

∴ ＝

9. 设数列的前项和为,且，（1）证明:数列是等比数列；

（2）若数列满足，，求数列的通项公式．解：（1）证：因为，则，所以当时，，

整理得． 5分由，令，得，解得．

所以是首项为1，公比为的等比数列． 7分

（2）解：因为，由，得． 9分

由累加得

9931()4423

n n A n =

-+?11(1)

993115651332()(1)14423344313

n n n n n n n T A n ?-+=-?=-+?--=-?-{}n a {}n b 111==b a 1073=+a a 3b 4a {}n a {}n b n n n b a c ?={}n c n n T {}n a d {}n b q 0>q 1073=+a a 105=a 55=a 11=a 4415==-d a a 1=d n d n a a n =-+=)1(13b 4a 41

==b b q 2=q 11

12--==n n n q

b b n a n =1

2-=n n b n n n b a c ?=1

-?n n n T 1

2102232221-?++?+?+?n n n T 2n n n n 22

)1(2322211

1?+?-++?+?+?- n T n

n n 222221210?-++++- n n n 22

21(1?---?12)1(-?-n n n T 12)1(+?-n

n {}n a n n S 34-=n n a S (1,2,)n = {}n a {}n b 1(1,2,)n n n b a b n +=+= 12b ={}n b 34-=n n a S (1,2,)n = 3411-=--n n a S (2,3,)n = 2n ≥1144n n n n n a S S a a --=-=-14

n n a a -=

34-=n n a S 1n =3411-=a a 11=a {}n a 4

4()3

n n

a -=1(1,2,)n n n

b a b n +=+= 1

14()3

n n n b b -+-=)()()(1231`21--++-+-+=n n n b b b b b b b b

＝，

（），当n=1时也满足，所以．

10.已知等差数列满足前2项的和为5，前6项的和为3. （1）求数列的通项公式；

（2）设，求数列的前项和。

解： (1)设等差数列的首项为，公差为d,则（2）

①②

①-②，得 —11分

一、选择题

1. 一个三角形的三个内角A 、B 、C 成等差数列，那么()tan A C +的值是（） A

．

．．不确定 2. 等差数列}{n a 的公差为2，若1a ，3a ，4a 成等比数列，则2a 等于( )

A 4-

B 6-

C 8-

D 10-

3. 等比数列｛a n ｝的前3项的和等于首项的3倍，则该等比数列的公比（） A ．－2 B ．1 C ．－2或1 D ．2或－1

4. 等差数列}a {n 中，已知前15项的和90S 15=，则8a 等于（）． A ．

45 B ．12

C ．

D ．6 5. 等比数列{}n a 中,0n a >,a 5a 6=9,则313233310log log log log a a a a +++???+=( )

A.12

B.10

C.8

D.32log 5+

6. 等比数列{a n } 的前n 项和为S n ，若S 4=1，S 8=4，则a 13+a 14+a 15+a 16=（）． A ．7 B ．16 C ．27 D ．64

7. 数列的通项公式，则该数列的前（）项之和等于

A B

C D

1)34(33

41)34(1211

-=--+--n n 2≥n 1)3

4(31

-=-n n b {}n a {}n a )(,2)4(*

∈?-=N n a b n

n n {}n b n n S {}n a 1a ??

???=?+=?+3

25665212211

d a d a ???-==1

d a 解得n d n a a n -=-+=∴4)1(1)(,22)4(*

∈?=?-=N n n a b n

n n 2222121n n n S ?++?+?= 13222)1(2221 2+?+?-++?+?=n n n n n S 1

222+?-++=-n n

n n S 122

21(2+?---=

n n n 22)1(1+?-=∴+n n n S {}n a 11

++=n n a n 9989697

8. 在等比数列{a n }中,a 5a 7=6,a 2+a 10=5,则

a a 等于( ) A.2

332--或 B.32 C.23 D.32或23

9. 等差数列,的前项和分别为,,若,则=（）

B C D 10. 已知数列}{n a 的前n 项和为)34()1(2117139511--++-+-+-=+n S n n ,

则312215S S S -+的值是（）

A. -76

B. 76

C. 46

D. 13

11. 知等差数列{}n a ，且410712a a a +=-，则数列{}n a 的前13项之和为 C A ．24 B ．39 C ．52D ．104

12. 设各项均不为0的数列{}n a 满足)1(21≥=+n a a n n ，若5422a a a =，则=3a D A.2 B.2 C.22 D.4

13. 已知等差数列{n a }的前n 项和为Sn ，若4518a a =-，则S 3= C A.54 B.68 C.72 D.90

14. 在等比数列中，200720108a a =，则公比q 的值为A

A. 2

B.3

C.4

D. 8

15. 已知等比数列满足：，，则的值是C

A. B. C. D.

16. 已知等差数列{}n a ，且410712a a a +=-，则数列{}n a 的前13项之和为 C A ．24 B ．39 C ．52D ．104

17. 公差不为零的等差数列第2，3，6项构成等比数列，则这三项的公比为C A ．1 B ．2 C ．3 D ．4

18. 已知数列{}n a 是公比为q 的等比数列，且1a ，3a ，2a 成等差数列，则q ＝ A

A.1或12-

B. 1

C.1

2- D.－2

19. 设是等差数列的前项和，若，则＝( A )

A ．1

B ．－1

C ．2

D ．

20. 已知等差数列{n a }的前n 项和为Sn ，若4518a a =-，则S 3= C

A.54

B.68

C.72

D.90 21. 在等比数列{}n a 中，若181564a a a =，则8a =D A. 16 B. 8 C. 22. 正项等比数列中，若

，则

等于 C

A.-16

B. 10

C. 16

D.256

{}n a {}n b n n S n T 231n n S n T n =+n n

a b 331n -31

n +34n +{}n a }{n a 354321=++++a a a a a 122524232221=++++a a a a a 54321a a a a a +-+-2941

n S {}n a n 65911

a a =119S

S 12

23. 已知正项等比数列{}n a 满足7652a a a =+。若存在两项,m n a a

14a =，则

m n +的最小值为B A 8

B 11

C 14

D 17

二、填空题

1. 数列?--,924

,715,58,1的一个通项公式是

2. 数列1111

1,2,3,,,2482

n n ++++……的前n 项和是

3. 在数列{}n a 中，11a =，且对于任意自然数n ，都有1n n a a n +=+，则100a ＝

4. 已知31=a ，n n a n n a 231

31+-=

+)1(≥n ， n a =_____________ 5. 已知数列的，则=_____________

6、等差数列{a n }中，39||||,a a =公差0,d <那么使前n 项和n S 最大的n 值为__________ 7. 已知数列{}n a 的前n 项和332n n S =-?，则n a =132n --?（*n N ∈）． 8. 已知数列{}n a 满足n a a a n n 2,3311=-=+，则n

a n 的最小值为____221______。

三、解答题

1. 已知数列的前项和，求

2. 已知数列{}n a 满足11

a =

, 112n n n n a a a a ++=-,求数列{}n a 的通项公式。

3. 数列{}n a 中，18a =，42a =，且满足2120n n n a a a ++-+=

（1）求数列{}n a 的通项公式；（2）设12||||||n n S a a a =+++ ，求n S 。

4. 已知}{n a 是等差数列，其前n 项和为S n ，已知,153,1193==S a （1）求数列}{n a 的通项公式

（2）设n n b a 2log =，证明}{n b 是等比数列，并求其前n 项和T n

++=n n S n 12111098a a a a a ++++{}n a n n

n S 23+=n

5. 已知数列{}n a 是等差数列，且12a =，12312a a a ++=.

⑴求数列{}n a 的通项公式； ⑵令n

n b a =?３*(N )n ∈，求数列{}n b 的前n 项和的公式.

6. 在等比数列中，，且，，成等差数列. （Ⅰ）求；

（Ⅱ）令，求数列的前项和.

解:（Ⅰ）设的公比为，由，，成等差数列，得.

又，则，解得. ∴（）. ··············· 6分

（Ⅱ），∴，是首项为0，公差为1的等差数列，

它的前项和. ································································12分

7. 已知等差数列{}n a 的前n 项和为n S ，且23a =，15225S =．（Ⅰ）求数列{}n a 的通项公式；

（Ⅱ）设22n a n b n =-，求数列{}n b 的前n 项和n T ．

解：（Ⅰ）设数列{}n a 的公差为d ，依题意得：

113,

1514

15225,2

a d a d +=??

??+=??解得11,2,a d =??=?∴数列{}n a 的通项公式21n a n =-． ···· 4分（Ⅱ）由（Ⅰ）得1

422n n b n =?-，

∴12n n T b b b =+++ 21

(444)2(12)2

n n =+++-+++ ········ 6分

12446

n n n +-=--222433n n n =?---． ·············· 12分

8. 在数列{}n a 中，1111

,33n n n a a a n

++==

（1）证明{}n a

是等比数列，并求{}n a 的通项公式；

（2）求{}n a 的前n 项和n S

解:(Ⅰ) ······································································ 2分 {}n a 11a =14a 22a 3a n a 2log n n b a ={}n b n n S {}n a q 14a 22a 3a 13244a a a +=11a =244q q +=2q =1

2n n a -=*N n ∈1

2log 21n n b n -==-11n n b b +-={}n b n (1)

n n n S -=1111,033n n n n a a a a n

++=

=∴> 1111==n 13n 13

n n a a

a +∴+ ，又

················································ 4分

······································································· 6分 (Ⅱ) ……① ························································ 7分

……② ···················································· 8分 ①-②得： ················································ 9分

323

443n

n +=-? 9. 等比数列{}n a 中，已知142,16a a == （I ）求数列{}n a 的通项公式；

（Ⅱ）若35,a a 分别为等差数列{}n b 的第3项和第5项，试求数列{}n b 的通项公式及前n 项和n S 。解：（I ）设{}n a 的公比为q

由已知得3

162q =，解得2q =，所以n n a 2=………………（5分）（Ⅱ）由（I ）得28a =，532a =，则38b =，532b =

设{}n b 的公差为d ，则有11

28432b d b d +=??+=?解得116

12b d =-??=?

从而1612(1)1228n b n n =-+-=-

所以数列{}n b 的前n 项和2(161228)

6222

n n n S n n -+-=

=-………（12分） 10. 已知各项均不相等的等差数列{n a }的前四项和为S 4＝14，且137,,a a a 成等比。（1）求数列{n a }的通项公式；

（2）设Tn 为数列11n n a a +??????

的前n 项和，若1n n T a λ+≤，对一切*

n N ∈恒成立，

求实数λ的最小值。

n n a ??

∴????

11为首项为，公比为的等比数列33n 1

n 11n ==n 333

n n a a -??∴?∴ ???，1231233333

n n n

S =++++ 231112133333

n n n n n

S +-∴=++++ 123121111333333

n n n n

S +=++++- 1111331313n n n +??- ???=--3114323

n n n n S ??∴=-- ???

11. 已知数列的首项且a n+1＝2a n +1(n ∈N *) （1）证明数列是等比数列，并求数列的通项公式；

（2）若，求函数在点处的导数

12. 已知数列是公差为正数的等差数列,其前项和为,点在抛物线

上；各项都为正数的等比数列满足. （I ）求数列，的通项公式；（II ）记,求数列的前n 项和. 解：（I ）当时，

………3分数列是首项为2，公差为3的等差数列 …4分

又各项都为正数的等比数列满足解得……………7分

(Ⅱ)1(31).()2

n c n ∴=-

211111

25()...(34)()(31)()2222

n n n T n n -∴=?+?++-?+-? ①

23111111

2()5()...(34)()(31)()22222n n n T n n +∴=?+?++-?+-?………② 10分 {}n a 2,511++

==+n s s a n n {}1+n a {}n a n

n x a x a x a x f +++= 221)()(x f 1=x )1('

f {}n a n n S (,)n n S 23122y x x =

+{}n b 13511,1632b b b =={}n a {}n b n n n C a b ={}n C n T 231

n S n n =

+ 1n =112a S ==2213135

2(1)(1)12222

n n S n n n n -≥=-+-=-+当时，131n n n a S S n -∴=-=-∴n a ｛｝31n a n ∴=- {}n b 13511

,432

b b b =

=421111

,432b b q b q ∴==

=111,22b q ==1()2

n b ∴=

① -②得

②

…12分

13. 已知等比数列{}n a 中，311=a ，公比3

=q 。

（1）n S 为{}n a 的前n 项和，证明：2

n a S -=；

（2）设n n a a a b 32313log ......log log +++=，求数列{}n b 的通项公式。

解：（1）证明：因为n n a 3

1n n S -

=，所以21n n

a S -=.

（2）解：2

)

1()21(log log log 32313+-

=+++-=+++=n n n a a a b n n 所以{b n }的通项公式为2

)

1(+-

=n n b n . 14. 设数列{}n a 为单调递增的等差数列，11a =，且1263,,a a a 依次成等比数列.

（Ⅰ）求数列{}n a 的通项公式n a ；

（Ⅱ）若2n a

n n b a =?，求数列{}n b 的前n 项和n S ；

（Ⅲ）若()

22322

a n a a c =+?+，求数列{}n c 的前n 项和n T ．

解：(Ⅰ)

()..121251.2363661236612n a d d d d

d a a a a a a a a n =∴=?+=+?==--==…….4分（Ⅱ）∵2

a n n n

b a n =?=?

∴231222322n n S n =?+?+?++?

23121222(1)22n n n S n n +=

?+?++-?+?

相减，得23122222n n n S n +-=++++-?

2(12)12

n -=-12n n +-?11222n n n ++=--?

∴1(1)22n n S n +=-?+． ……………….13分

（Ⅲ）()()()()()121122211

.2121

212221212322n

n n n n n n n n n n n

c ---====-+++++++?+则231

1111113[()()...()](31)()22222

n n n T n +∴=++++--?11

11[1()]

14213(31)()1212

n n n -+-=+?--?-1511

3()(31)()222n n n +=

-?--?35

n n n T +∴=-

0112111111

111.212121212121221n n n n

T -??????=-+-++-=- ? ? ?+++++++??????

…13分

15. 已知是等差数列，其前n 项和为S n ，是等比数列，

且， .

（Ⅰ）求数列与的通项公式；

（Ⅱ）记，，证明（）解：（I ）31n a n =-；2n n b =. ……6分

（II ）错位相减法T=n 102610n ?--……（文）12分（理）10分

T+12=102-6n+2 -2a+10b=102-6n+2 …… (理)12分

16. 已知数列{}满足．

（1）证明：数列{+2}是等比数列．并求数列{}的通项公式；

（2）若数列满足，设是数列的前项和．求证：解：证明：（1）由a n =2a n-1+2，

∴

又，

∴ ∴，

∴

（2）证明：由

则③

④

③-④，得

所以：．

}{n a }{n b 27,24411=+==b a b a 1044=-b S }{n a }{n b n n n n b a b a b a T 1211+++=- *

N n ∈n n n b a T 10212+-=+*

N n ∈n a 112,22(2)n n a a a n -==+≥n a n a n a {}n b 2log (2)=+n n b a n T }2

{+n n

a b n 32n

T <122(2)+=+－n n a a .22

1=++-n n a a 12=a {}1224n a a ++=是以为首项，以2为公比的等比数列1

2=42n n a -+?1

2n n a -=?-,2

2,12

log )2(log 11

22+++=++==+=n n n n n n n a b n a b 得23412121111222222

n n n n T +++=++++-

L 12

323++-=n n n T 32

17. 已知数列{}n a 的前n 项和为n S ，且22n n S a =-．（Ⅰ）求数列{}n a 的通项公式；

（Ⅱ）令12

l o g n n n b n a a =+，数列{}n b 的前n 项和为n T ，求使不等式(1)(2)430n n T n S --++<成

立的正整数n 的最小值．解：（Ⅰ）当1n =时，1122a a =-，解得12a =；

当2n ≥时，11122(22)22n n n n n n n a S S a a a a ---=-=---=-，

∴12n n a a -=，故数列{}n a 是以12a =为首项，2为公比的等比数列，

故1222n n n a -=?=． ········································································ 4分（Ⅱ）由（Ⅰ）得，12

2log 22n n n n b n n n =?+=?-，

∴2

312(222322)(12)n n n T b b b n n =+++=+?+?++?-+++ ， ········· 5分令23222322n n R n =+?+?++? ，则23412222322n n R n +=+?+?++? ，

两式相减得2

12(12)22222212

n n

n n n R n n ++--=++++-?=-?-

∴1(1)22n n R n +=-+， ··································································· 7分

∴112(1)

(1)222

n n n n n T b b b n ++=+++=-+- ， ································· 8分

又由（Ⅰ）得，12222n n n S a +=-=-， ············································· 9分

不等式(1)(2)430n n T n S --++<即为：11(1)

(1)22(1)24302

n n n n n n +++-+---+<，

∴2

900n n +->， ········································································ 10分解得9n >或10n <-， ··································································· 11分因为*n ∈N ，故使不等式1(1)430n n T n a +--+<成立的正整数n 的最小值为10

18. 已知n S 是等比数列{}n a 的前n 项和，693,,S S S 成等差数列. （Ⅰ）求数列{}n a 的公比q ；（Ⅱ）证明：582,,a a a 成等差数列.

解：（Ⅰ）由S 3，S 9，S 6成等差数列，可得2 S 9=S 3+S 6．

当q =1时，即得1111836a a a ≠+，不成立．……………………………………3分

当1q ≠时，即得9361112(1)(1)(1)

111a q a q a q q q q

---=+---，

整理得：63210q q --=，即3232()10q q --=，

解得：1q =（舍去），或q =7分（Ⅱ）证明：由（Ⅰ）知3612q q +=，

∴4325111(1)a a a q a q a q q +=+=+671122a q q a q =?=，

∵78122a a q =，

∴2582a a a +=，即a 2，a 8，a 5成等差数列．………………………………12分 19. 数列{n a }的前n 项和n S 满足：*23()n n S a n n N =-∈．（Ⅰ）求数列{n a }的通项公式n a ；

（Ⅱ）令9

++=

n S b n n ，数列{n b } 的前n 项和为n T ，求证：21

高中数学数列专题大题训练

高中数学数列专题大题组卷一．选择题（共9小题） 1．等差数列{a n}的前m项和为30，前2m项和为100，则它的前3m项和为（）A．130 B．170 C．210 D．260 2．已知各项均为正数的等比数列{a n}，a1a2a3=5，a7a8a9=10，则a4a5a6=（）A．B．7 C．6 D． 3．数列{a n}的前n项和为S n，若a1=1，a n+1=3S n（n≥1），则a6=（） A．3×44B．3×44+1 C．44D．44+1 4．已知数列{a n}满足3a n+1+a n=0，a2=﹣，则{a n}的前10项和等于（）A．﹣6（1﹣3﹣10）B．C．3（1﹣3﹣10）D．3（1+3﹣10）5．等比数列{a n}的前n项和为S n，已知S3=a2+10a1，a5=9，则a1=（）A．B．C．D． 6．已知等差数列{a n}满足a2+a4=4，a3+a5=10，则它的前10项的和S10=（）A．138 B．135 C．95 D．23 7．设等差数列{a n}的前n项和为S n，若S m﹣1=﹣2，S m=0，S m+1=3，则m=（）A．3 B．4 C．5 D．6 8．等差数列{a n}的公差为2，若a2，a4，a8成等比数列，则{a n}的前n项和S n=（） A．n（n+1）B．n（n﹣1）C．D． 9．设{a n}是等差数列，下列结论中正确的是（） A．若a1+a2＞0，则a2+a3＞0 B．若a1+a3＜0，则a1+a2＜0 C．若0＜a 1＜a2，则a2D．若a1＜0，则（a2﹣a1）（a2﹣a3）＞0 二．解答题（共14小题） 10．设数列{a n}（n=1，2，3，…）的前n项和S n满足S n=2a n﹣a1，且a1，a2+1，a3成等差数列．

高三数学数列专题复习题含答案

高三数学数列专题复习题含答案一、选择题 1.等比数列{}n a 中，12a =，8a =4，函数 ()128()()()f x x x a x a x a =---L ，则()'0f =（） A ．62 B. 92 C. 122 D. 152 【答案】C 【解析】考查多项式函数的导数公式，重点考查学生创新意识，综合与灵活地应用所学的数学知识、思想和方法。考虑到求导中，含有x 项均取0，则()' 0f 只与函数()f x 的一次项有关；得：412 123818()2a a a a a a ??==L 。 2、在等比数列{}n a 中，11a =，公比1q ≠.若12345m a a a a a a =，则m= （A ）9 （B ）10 （C ）11 （D ）12 【答案】C 3、已知{}n a 是首项为1的等比数列，n s 是{}n a 的前n 项和，且369s s =，则数列1n a ?? ???? 的前5项和为（A ） 158或5 （B ）3116或5 （C ）3116 （D ）15 8 【答案】C 【解析】本题主要考查等比数列前n 项和公式及等比数列的性质，属于中等题。显然q ≠1，所以3639(1q )1-=121-q 1q q q q -?+?=-，所以1{}n a 是首项为1，公比为1 2 的等比数列，前5项和5 51 1()31211612 T -= =-. 4、已知各项均为正数的等比数列{n a }，123a a a =5，789a a a =10，则456a a a = (A) 【答案】A

【解析】由等比数列的性质知31231322()5a a a a a a a ===g ，3 7897988()a a a a a a a ===g 10,所以 13 2850a a =, 所以13 3 3 64564655 28()()(50)52a a a a a a a a a =====g 5.已知等比数列{m a }中，各项都是正数，且1a ， 321 ,22 a a 成等差数列，则91078a a a a +=+ A.12+ B. 12- C. 322+ D 322- 6、设{}n a 是任意等比数列，它的前n 项和，前2n 项和与前3n 项和分别为,,X Y Z ，则下列等式中恒成立的是 A 、2X Z Y += B 、()()Y Y X Z Z X -=- C 、2 Y XZ = D 、()()Y Y X X Z X -=- 【答案】 D 【分析】取等比数列1,2,4,令1n =得1,3,7X Y Z ===代入验算，只有选项D 满足。 8、设等差数列{}n a 的前n 项和为n S ,若111a =-,466a a +=-,则当n S 取最小值时,n 等于 A ．6 B ．7 C ．8 D ．9 【答案】A 【解析】设该数列的公差为d ，则461282(11)86a a a d d +=+=?-+=-，解得2d =，所以22(1) 11212(6)362 n n n S n n n n -=-+ ?=-=--，所以当6n =时，n S 取最小值。 9、已知等比数列{}n a 满足0,1,2,n a n >=L ，且25252(3)n n a a n -?=≥，则当1n ≥时， 2123221log log log n a a a -+++=L A. (21)n n - B. 2 (1)n + C. 2n D. 2 (1)n -

高中数学数列综合专项练习讲义

高中数学数列综合专项练习讲义 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】

专题数列综合考点精要会求简单数列的通项公式和前n 项和．热点分析数列的通项和求和，历来是高考命题的常见考查内容．要重点掌握错位相减法，灵活运用裂项相消法，熟练使用等差和等比求和公式，掌握分组求和法．知识梳理 1.数列的通项求数列通项公式的常用方法：（1）观察与归纳法：先观察哪些因素随项数n 的变化而变化，哪些因素不变：分析符号、数字、字母与项数n 在变化过程中的联系，初步归纳公式。（2）公式法：等差数列与等比数列。（3）利用n S 与n a 的关系求n a ：则???≥-==-2111 n S S n S a n n n （注意：不能忘记讨论1=n ）（4）逐项作差求和法（累加法）；已知)2)((1≥=--n n f a a n n ，且{f(n)}的和可求，则求n a 可用累加法（5）逐项作商求积法（累积法）;已知 )2)((1 ≥=-n n f a a n n ，且{f(n)}的和可求，求n a 用累乘法. （6）转化法 2几种特殊的求通项的方法（一）1n n a ka b +=+型。（1）当1k =时，{}1n n n a a b a +-=?是等差数列，1()n a bn a b =++ （2）当1k ≠时，设1()n n a m k a m ++=+，则{}n a m +构成等比数列，求出{}n a m +的通项，进一步求出{}n a 的通项。例：已知{}n a 满足111,23n n a a a +==-，求{}n a 的通项公式。

高中数学数列放缩专题：用放缩法处理数列和不等问题

用放缩法处理数列和不等问题（教师版）一．先求和后放缩（主要是先裂项求和，再放缩处理）例1．正数数列{}n a 的前n 项的和n S ，满足12+=n n a S ，试求：（1）数列{}n a 的通项公式；（2）设11+= n n n a a b ，数列{}n b 的前n 项的和为n B ，求证：2 1

(完整版)高三文科数学数列专题.doc

高三文科数学数列专题高三文科数学复习资料 ——《数列》专题 1. 等差数列{ a n}的前n项和记为S n，已知a1030, a2050 . （ 1）求通项a n；（ 2）若S n242 ，求 n ；（ 3）若b n a n20 ，求数列 { b n } 的前 n 项和 T n的最小值. 2. 等差数列{ a n}中，S n为前n项和，已知S77, S1575 . （ 1）求数列{ a n}的通项公式；（ 2）若b n S n，求数列 {b n } 的前 n 项和 T n. n 3. 已知数列{ a n}满足a1 1 a n 1 ( n 1) ，记 b n 1 ， a n . 1 2a n 1 a n （1）求证 : 数列{ b n}为等差数列；（2）求数列{ a n}的通项公式 . 4. 在数列a n 中， a n 0 ， a1 1 ，且当 n 2 时，a n 2S n S n 1 0 . 2 （ 1）求证数列1 为等差数列；S n （ 2）求数列a n的通项 a n；（ 3）当n 2时，设b n n 1 a n，求证： 1 2 (b2 b3 b n ) 1 . n 2(n 1) n 1 n 5. 等差数列{ a n}中，a18, a4 2 . （ 1）求数列{ a n}的通项公式；（ 2）设S n| a1 | | a2 || a n |，求 S n；

1 (n N *) ， T n b1 b2 b n (n N *) ，是否存在最大的整数m 使得对任（ 3）设b n n(12 a n ) 意 n N * ，均有T n m m 的值，若不存在，请说明理由. 成立，若存在，求出 32 6. 已知数列{log2(a n1)} 为等差数列，且a13, a39 . （ 1）求{ a n}的通项公式；（ 2）证明： 1 1 ... 1 1. a2 a1 a3 a2 a n 1 a n 7. 数列{ a n}满足a129, a n a n 12n 1(n 2, n N * ) . （ 1）求数列{ a n}的通项公式；（ 2）设b n a n，则 n 为何值时， { b n } 的项取得最小值，最小值为多少？n 8. 已知等差数列{ a n}的公差d大于0 , 且a2,a5是方程x2 12 x 27 0 的两根,数列 { b n } 的前 n 项和为 T n,且 T n 1 1 b n. 2 （ 1）求数列{ a n} , { b n}的通项公式；（ 2）记c n a n b n，求证:对一切 n N 2 , 有c n. 3 9. 数列{ a n}的前n项和S n满足S n2a n 3n . （1）求数列{ a n}的通项公式a n；（2）数列{ a n}中是否存在三项，它们可以构成等差数列？若存在，请求出一组适合条件的项；若不存在，请说明理由 . 10. 已知数列{ a n}的前n项和为S n，设a n是S n与 2 的等差中项，数列{ b n} 中， b1 1，点 P(b n , b n 1 ) 在直线 y x 2 上. （ 1）求数列{ a n} , { b n}的通项公式

高中数学全国卷数列专题复习.doc

数列专题复习（ 1）一、等差数列和等比数列的性质 1、已知 { a n } 是公差为 1 的等差数列， S n 为 { a n } 的前 n 项和，若 S 8 4S 4 ，则 a 10 17 （ B ） 19 （ C ） 10 （D ） 12 （ A ） 2 2 2、数列 a n 中 a 1 2,a n 1 2a n , S n 为 a n 的前 n 项和，若 S n 126 ，则 n 3、设 S n 是等差数列 { a n } 的前 n 项和 ,若 a 1 a 3 a 5 3 ,则 S 5 A 5 B 7 C 9 D 11 4、已知等比数列 { a } 满足 a 1 1 , a 3 a 5 4 a 4 1 ,则 a A. 2 B.1 C. 1 D. 1 n 4 2 2 8 5、等比数列｛ a n ｝满足 a 1=3， a 1 a 3 a 5 =21，则 a 3 a 5 a 7 A21 B42 C63 D84 6、等差数列 a n 的公差为 2，若 a 2 ， a 4 ， a 8 成等比数列，则 a n 的前 n 项和 S n = （ A ） n n 1 （ B ） n n 1 （ C ） n n 1 n n 1 2 (D) 2 7、设等差数列 {a } 的前 n 项和为 S ，若 S ＝－ 2，S ＝ 0，S ＝ 3，则 m ＝ n n m － 1 m m ＋ 1 A ． 3 B ． 4 C ． 5 D ．6 8、等比数列｛ a ｝的前 n 项和为 S ，已知 S = a +10a ， a = 9，则 a = n n 3 2 1 5 1 （ A ） 1 （ B ） 1 （ C ） 1 （ D ） 1 3 3 9 9 9、已知 { a n }为等比数列， a 4 a 7 2 ， a 5 a 6 8 ，则 a 1 a 10 A7 B5 C － 5 D －7 10、已知各项均为正数的等比数列 { a n } ， a 1a 2a 3 =5， a 7a 8 a 9 =10，则 a 4 a 5 a 6 = (A) 5 2 (B) 7 (C) 6 (D) 4 2 11、如果等差数列 { a n } 中， a 3 a 4 a 5 12 ，那么 a 1 a 2 ... a 7 （A ）14 （B ）21 （ C ） 28 （D ） 35 12、等差数列 { a n } 的前 n 项和为 S n ，已知 S 10=0，S 15 =25 ，则 nS n 的最小值为 ________. 13、等比数列 { a n } 的前 n 项和为 S n ，若 S 3 3S 2 0 ，则公比 q ___________。 14、设 S n 为等差数列 a n 的前 n 项和，若 a 1 =1，公差 d=2 ， S k+2-S k =24 ，则 k= (A)8 (B)7 (C) 6 (D) 5 15、设△ A n B n C n 的三边长分别为 a n ， b n ， c n ，△ A n B n C n 的面积为 S n ，n ＝ 1,2,3，? .若 b 1＞ c 1， 11 1 n ＋ 1 n n ＋ 1 ＝ c n a n ， c n ＋1 b n a n ，则 ( )． b ＋ c ＝2a ， a ＝ a ， b ＝ 2 2

高中数学数列知识点总结(经典)

数列基础知识点和方法归纳 1. 等差数列的定义与性质定义：1n n a a d +-=（d 为常数），()11n a a n d =+- 等差中项：x A y ，，成等差数列2A x y ?=+ 前n 项和()() 1112 2 n n a a n n n S na d +-= =+ 性质：{}n a 是等差数列（1）若m n p q +=+，则m n p q a a a a +=+；（2）数列{}{}{}12212,,+-n n n a a a 仍为等差数列，232n n n n n S S S S S --，，……仍为等差数列，公差为d n 2；（3）若三个成等差数列，可设为a d a a d -+，，（4）若n n a b ，是等差数列，且前n 项和分别为n n S T ，，则 21 21 m m m m a S b T --= （5）{}n a 为等差数列2n S an bn ?=+（a b ，为常数，是关于n 的常数项为0的二次函数） n S 的最值可求二次函数2n S an bn =+的最值；或者求出{}n a 中的正、负分界项，即：当100a d ><，，解不等式组10 0n n a a +≥??≤?可得n S 达到最大值时的n 值. 当100a d <>，，由10 0n n a a +≤??≥?可得n S 达到最小值时的n 值. (6)项数为偶数n 2的等差数列{} n a ，有 ),)(()()(11122212为中间两项++-+==+=+=n n n n n n n a a a a n a a n a a n S nd S S =-奇偶， 1 += n n a a S S 偶奇. （7）项数为奇数12-n 的等差数列{} n a ，有

高中数学~数列专题复习

高中数学必修五数列专题复习主备人：海门实验施庆主备人心语~数学考试心理辅导模块 1.调整心态：强化必胜信心、优化跃跃欲试的应考情绪，进入应考状态，充分发挥自身水平。 2.强调策略：每做一题，不急于动手，先看清题设条件，挖掘隐晦信息；仔细分析题目，选择正确思路解答；越是似曾相识的题目越要冷静对待。 3.梳理思路：强化答题格式，推敲得分点，增强得分意识，解剖试题命题点，摸清问题的指向。复习容如下考点1：数列的有关概念 1．在数列{}n a 中，12a =， 11ln(1)n n a a n +=++，则n a = 1．解：A ． 211ln(1)1 a a =++，321ln(1)2a a =++，…，11ln(1)1n n a a n -=++- 1234ln()()()()2ln 1231 n n a a n n ?=+=+- 2．已知)(156 2*∈+=N n n n a n ，则数列{}n a 的最大项是 2．解：数列可以看成一种特殊的函数即)(156 2*∈+=N n n n a n 可以看成 2 ()()156 X f X X N X += ∈+通过求函数的最大值可知第12项和第13项最大． 3．在数列{}n a 中， 23312n n a n ++ =++，()n *∈N ，在数列{}n b 中，)cos(πn n a b =， ()n *∈N ，则2008 2009b b -=_________． 3解：n a 的奇偶性为：奇，奇，偶，偶，奇，奇，偶，偶，…，从而n b 分别为： 1-，1-，1，1，1-，1-， 1，1，…，周期为4，所以，2008 20091(1)2b b -=--=．答： 2 4．已知数列}{n a 的通项公式为n a ＝12 n +，设1324 2 11 1n n n T a a a a a a += +++???，求n T ． 4．解： 2 1 n n a a +?＝ 4 (1)(3)n n ++＝2（11n +－13 n +）． 1324 2 11 1n n n T a a a a a a +=++ + ???＝2[（12－14 ）＋（13 －15 ）＋（14 －16 ）＋……＋（1 n

高中数学数列讲义总结

09级高三数学总复习讲义——数列概念知识清单 1．数列的概念（1）数列定义：按一定次序排列的一列数叫做数列；数列中的每个数都叫这个数列的项。记作n a ，在数列第一个位置的项叫第1项（或首项），在第二个位置的叫第2项，……，序号为n 的项叫第n 项（也叫通项）记作n a ；数列的一般形式：1a ，2a ，3a ，……，n a ，……，简记作 {}n a 。（2）通项公式的定义：如果数列}{n a 的第n 项与n 之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式。例如，数列①的通项公式是n a = n （n ≤7，n N +∈），数列②的通项公式是n a = 1 n （n N +∈）。说明： ①{}n a 表示数列，n a 表示数列中的第n 项，n a = ()f n 表示数列的通项公式； ② 同一个数列的通项公式的形式不一定唯一。例如，n a = (1)n -=1,21 ()1,2n k k Z n k -=-?∈?+=?； ③不是每个数列都有通项公式。例如，1，1.4，1.41，1.414，…… （3）数列的函数特征与图象表示：序号：1 2 3 4 5 6 项：4 5 6 7 8 9 上面每一项序号与这一项的对应关系可看成是一个序号集合到另一个数集的映射。从函数观点看，数列实质上是定义域为正整数集N +（或它的有限子集）的函数()f n 当自变量n 从1开始依次取值时对应的一系列函数值(1),(2),(3),f f f ……，()f n ，……．通常用n a 来代替 ()f n ，其图象是一群孤立点。（4）数列分类：①按数列项数是有限还是无限分：有穷数列和无穷数列；②按数列项与项之间的大小关系分：单调数列（递增数列、递减数列）、常数列和摆动数列。（5）递推公式定义：如果已知数列{}n a 的第1项（或前几项），且任一项n a 与它的前一项1n a -（或前几项）间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的递推公式。（6）数列{n a }的前n 项和n S 与通项n a 的关系：1 1(1)(2)n n n S n a S S n -=?=?-?≥ 课前预习 1．根据数列前4项，写出它的通项公式：（1）1，3，5，7……；（2）2212-，2313-，2414 -，2515-；（3）11*2-，12*3，13*4-，1 4*5 。 2．数列{}n a 中，已知21 ()3n n n a n N ++-= ∈，（1）写出10a ，1n a +，2n a ；

备战高考技巧大全之高中数学黄金解题模板：专题26 数列求和方法答案解析

【高考地位】数列是高中数学的重要内容,又是高中数学与高等数学的重要衔接点,其涉及的基础知识、数学思想与方法,在高等数学的学习中起着重要作用,因而成为历年高考久考不衰的热点题型,在历年的高考中都占有重要地位。数列求和的常用方法是我们在高中数学学习中必须掌握的基本方法，是高考的必考热点之一。此类问题中除了利用等差数列和等比数列求和公式外，大部分数列的求和都需要一定的技巧。下面，就近几年高考数学中的几个例子来谈谈数列求和的基本方法和技巧。【方法点评】方法一公式法解题模板：第一步结合所求结论，寻找已知与未知的关系；第二步根据已知条件列方程求出未知量；第三步利用前n 项和公式求和结果例1.设}{n a 为等差数列，n S 为数列}{n a 的前n 项和，已知77=S ，7515=S ，n T 为数列}{n S n 的前n 项和，求n T ．【评析】直接应用公式求和时，要注意公式的应用范围，如当等比数列公比为参数(字母)时，应对其公比是否为1进行讨论．常用的数列求和公式有：

等差数列前n 项和公式： 11()(1)22 n n n a a n n S na d +-==+．等比数列前n 项和公式：111(1)(1)(1)11n n n na q S a q a a q q q q =??=--?=≠?--? ．自然数方幂和公式：1123(1)2 n n n +++???+=+ 22221123(1)(21)6 n n n n +++???+=++ 333321123[(1)]2 n n n +++???+=+ 【变式演练1】已知{a n }是等差数列，a 1+a 2=4，a 7+a 8=28，则该数列前10项和S 10等于（） A.64 B.100 C.110 D.120 【答案】B 【解析】试题分析：a 1+a 2=4，a 7+a 8=28，解方程组可得11,2a d == 101109101002 S a d ?∴=+ = 考点：等差数列通项公式及求和方法二分组法解题模板：第一步定通项公式：即根据已知条件求出数列的通项公式；第二步巧拆分：即根据通项公式特征，将其分解为几个可以直接求和的数列；第三步分别求和：即分别求出各个数列的和；第四步组合：即把拆分后每个数列的求和进行组合，可求得原数列的和. 例2. 已知数列{a n }是3＋2－1,6＋22－1,9＋23－1,12＋24－1，…，写出数列{a n }的通项公式并求其前n 项 S n .

人教版最新高中数学数列专题复习(综合训练篇含答案)Word版

——教学资料参考参考范本——人教版最新高中数学数列专题复习(综合训练篇含答案)Word 版 ______年______月______日 ____________________部门

———综合训练篇一、选择题： 1．在等差数列中，，则的值为（ D ）{}n a 120 31581=++a a a 1092a a - A ．18 B ．20 C ．22 D ．24 2．等差数列满足：，若等比数列满足则为（ B ） A ．16 B ．32 C ．64 D ．27{}n a 30,8531==+S a a {} n b ,,4311a b a b ==5b 3．等差数列中,则数列的前9项之和S9等于{} n a 1 a {a （ C ）A ．66 B ．144 C ．99 D ．297 4．各项都是正数的等比数列的公比q ≠1，且，，成等差数列，则为（A ） A ． B ． C ． D ．或{} n a 2a 321a 1 a 5 443a a a a ++2 15-215+2 51-2 1 5+215- 5.设等比数列的前项和为，若则（ B ）{}n a n n S ,33 6=S S = 69S S A. 2 B. C. D.3738 3

6．已知等差数列的前项的和为，且，，则过点和的直线的一个方向向量的坐标是 ( B ){}n a n n S 210S =555S =(,) n P n a 2(2,)()n Q n a n N *++∈ A. B. C. D.1(2,)2 1(,2)2--1(,1) 2--(1,1)-- 7．设a 、b 、c 为实数,3a 、4b 、5c 成等比数列,且、、成等差数列，则的值为（ C ） A ． B ． C ． D ．a 1b 1c 1a c c a +15941594±15341534 ± 8．已知数列的通项则下列表述正确的是 ( A ){} n a ,1323211 ????????-??? ??? ? ? ??=--n n n a A ．最大项为最小项为 B ．最大项为最小项不存在,1a 3 a ,1a C ．最大项不存在，最小项为 D ．最大项为最小项为3 a ,1a 4a 9.已知为等差数列，++=105，=99.以表示的前项和，则使得达到最大值的是（B ）{}n a 1a 3a 5a 246a a a ++n S {}n a n n S n A ．21 B ．20 C ．19 D ．18 9．一系列椭圆都以一定直线l 为准线，所有椭圆的中心都在定点M ，且点M 到l 的距离为2，若这一系列椭圆的离心率组成以为首项，为公比的等比数列，而椭圆相应的长半轴长为ai=(i=1，2，…，n)，设bn=2（2n+1）·3n －2·an ，且Cn=，Tn=C1+C2+…+Cn ，若

高中数学数列复习题型归纳解题方法整理

数列一、等差数列与等比数列 1.基本量的思想：常设首项、（公差）比为基本量，借助于消元思想及解方程组思想等。转化为“基本量”是解决问题的基本方法。 2.等差数列与等比数列的联系 1）若数列{}n a 是等差数列，则数列}{n a a 是等比数列，公比为d a ，其中a 是常数，d 是{}n a 的公差。（a>0且a ≠1）； 2）若数列{}n a 是等比数列，且0n a >，则数列{}log a n a 是等差数列，公差为log a q ，其中a 是常数且 0,1a a >≠，q 是{}n a 的公比。 3）若{}n a 既是等差数列又是等比数列,则{}n a 是非零常数数列。 3.等差与等比数列的比较

4、典型例题分析【题型1】等差数列与等比数列的联系例1 （2010陕西文16）已知{}是公差不为零的等差数列，a1＝1，且a1，a3，a9成等比数列.（Ⅰ）求数列{}的通项;（Ⅱ）求数列{2}的前n项和. 解：（Ⅰ）由题设知公差d≠0，由a1＝1，a1，a3，a9成等比数列得12 1 d + ＝ 18 12 d d + + ，解得d＝1，d＝0（舍去），故{}的通项＝1+（n－1）×1＝n. (Ⅱ)由（Ⅰ）知2m a=2n，由等比数列前n项和公式得 2+22+23+…+22(12) 12 n - - 21-2. 小结与拓展：数列{}n a是等差数列，则数列} {n a a是等比数列，公比为d a，其中a是常数，d是{}n a的公差。（a>0且a≠1）. 【题型2】与“前n项和与通项”、常用求通项公式的结合例2 已知数列{}的前三项与数列{}的前三项对应相同，且a1＋2a2＋22a3＋…＋2n－1＝8n对任意的n∈N*都成立，数列{＋1－}是等差数列．求数列{}与{}的通项公式。解：a1＋2a2＋22a3＋…＋2n－1＝8n(n∈N*) ① 当n≥2时，a1＋2a2＋22a3＋…＋2n－2－1＝8(n－1)(n∈N*) ② ①－②得2n－1＝8，求得＝24－n，在①中令n＝1，可得a1＝8＝24－1， ∴＝24－n(n∈N*)．由题意知b1＝8，b2＝4，b3＝2，∴b2－b1＝－4，b3－b2＝－2， ∴数列{＋1－}的公差为－2－(－4)＝2，∴＋1－＝－4＋(n－1)×2＝2n－6，

高中数学竞赛_数列【讲义】

第五章数列一、基础知识定义1 数列，按顺序给出的一列数，例如1，2，3，…，n ，…. 数列分有穷数列和无穷数列两种，数列{a n }的一般形式通常记作a 1, a 2, a 3,…，a n 或a 1, a 2, a 3,…，a n …。其中a 1叫做数列的首项，a n 是关于n 的具体表达式，称为数列的通项。定理1 若S n 表示{a n }的前n 项和，则S 1=a 1, 当n >1时，a n =S n -S n -1. 定义2 等差数列，如果对任意的正整数n ，都有a n +1-a n =d （常数），则{a n }称为等差数列，d 叫做公差。若三个数a , b , c 成等差数列，即2b =a +c ，则称b 为a 和c 的等差中项，若公差为d, 则a =b -d, c =b +d. 定理2 等差数列的性质：1）通项公式a n =a 1+(n -1)d ；2）前n 项和公式： S n =d n n na a a n n 2 )1(2)(11-+=+；3）a n -a m =(n -m)d ，其中n , m 为正整数；4）若n +m=p +q ，则a n +a m =a p +a q ；5）对任意正整数p , q ，恒有a p -a q =(p -q )(a 2-a 1)；6）若A ，B 至少有一个不为零，则{a n }是等差数列的充要条件是S n =An 2+Bn . 定义3 等比数列，若对任意的正整数n ，都有 q a a n n =+1，则{a n }称为等比数列，q 叫做公比。定理3 等比数列的性质：1）a n =a 1q n -1 ；2）前n 项和S n ，当q ≠1时，S n =q q a n --1)1(1；当q =1时，S n =na 1；3）如果a , b , c 成等比数列，即b 2=ac (b ≠0)，则b 叫做a , c 的等比中项；4）若m+n =p +q ，则a m a n =a p a q 。定义4 极限，给定数列{a n }和实数A ，若对任意的ε>0，存在M ，对任意的n >M(n ∈N ),都有|a n -A |<ε，则称A 为n →+∞时数列{a n }的极限，记作.lim A a n n =∞ → 定义5 无穷递缩等比数列，若等比数列{a n }的公比q 满足|q |<1，则称之为无穷递增等比数列，其前n 项和S n 的极限（即其所有项的和）为q a -11（由极限的定义可得）。定理3 第一数学归纳法：给定命题p (n )，若：（1）p (n 0)成立；（2）当p (n )时n =k 成立时能推出p (n )对n =k +1成立，则由（1），（2）可得命题p (n )对一切自然数n ≥n 0成立。竞赛常用定理定理4 第二数学归纳法：给定命题p (n )，若：（1）p (n 0)成立；（2）当p (n )对一切n ≤k 的自然数n 都成立时（k ≥n 0）可推出p (k +1)成立，则由（1），（2）可得命题p (n )对一切自然数n ≥n 0成立。定理5 对于齐次二阶线性递归数列x n =ax n -1+bx n -2，设它的特征方程x 2=ax +b 的两个根为α,β:(1)若α≠β，则x n =c 1a n -1+c 2βn -1，其中c 1, c 2由初始条件x 1, x 2的值确定；(2)若α=β，则x n =(c 1n +c 2) αn -1，其中c 1, c 2的值由x 1, x 2的值确定。二、方法与例题 1．不完全归纳法。这种方法是从特殊情况出发去总结更一般的规律，当然结论未必都是正确的，但却是人类探索未知世界的普遍方式。通常解题方式为：特殊→猜想→数学归纳法证明。例1 试给出以下几个数列的通项（不要求证明）；1）0，3，8，15，24，35，…；2）1，5，19，65，…；3）-1，0，3，8，15，…。【解】1）a n =n 2-1；2）a n =3n -2n ；3）a n =n 2-2n . 例2 已知数列{a n }满足a 1= 21,a 1+a 2+…+a n =n 2a n , n ≥1，求通项a n . 【解】因为a 1= 2 1,又a 1+a 2=22·a 2,

高中数学数列求和专题复习知识点习题.doc

数列求和例题精讲 1．公式法求和（1）等差数列前 n 项和公式 S n n(a 1 a n ) n(a k 1 a n k ) n( n 1) d 2 2 na 1 2 （2）等比数列前 n 项和公式 q 1 时 S n na 1 q 1 时 S n a 1 (1 q n ) a 1 a n q 1 q 1 q （3）前 n 个正整数的和 1 2 3 n(n 1) n 2 前 n 个正整数的平方和 12 22 32 n 2 n(n 1)(2n 1) 6 前 n 个正整数的立方和 13 23 33 n 3 [ n(n 1) ] 2 （ 1）弄准求和项数 n 的值； 2 公式法求和注意事项（ 2）等比数列公比 q 未知时，运用前 n 项和公式要分类。例 1．求数列 1，4，7，，3n 1 的所有项的和例 2．求和 1 x x 2 x n 2 ( n 2, x 0 )

2．分组法求和例 3．求数列 1， 1 2，1 2 3，，1 2 3 n 的所有项的和。 5n 1 (n为奇数 ) 例 4．已知数列a n中，a n ，求 S2m。 ( 2) n (n为偶数 ) 3．并项法求和例 5．数列a n 中， a n ( 1) n 1 n2，求 S100。例 6．数列a n中，，a n( 1) n 4n ，求 S20及 S35。 4．错位相减法求和若a n 为等差数列，b n 为等比数列，求数列a n b n（差比数列）前n项 b n 的公比。和，可由S n qS n求 S n，其中q 为

例 7．求和12x 3x 2nx n 1（x0 ）。 5．裂项法求和 :把数列各项拆成两项或多项之和，使之出现成对互为相反数的项。例 8．求和 1 1 1 1 。 1 3 3 5 5 7 (2n 1)(2n 1) 例 9．求和 1 1 1 1 2 1 3 2 23 。 n 1n ［练习］ 1 1 1 1 1 2 3 2 3 n 1 2 1 a n S n 2 1 n 1

高三数列专题练习30道带答案

高三数列专题训练二学校:___________姓名：___________班级：___________考号：___________ 一、解答题 1．在公差不为零的等差数列{}n a 中，已知23a =，且137a a a 、、成等比数列．（1）求数列{}n a 的通项公式；（2）设数列{}n a 的前n 项和为n S ，记，求数列{}n b 的前n 项和n T ． 2．已知等差数列{}n a 的前n 项和为n S ，公差,50,053=+≠S S d 且1341,,a a a 成等比数列. （Ⅰ）求数列{}n a 的通项公式； 1，公比为3的等比数列，求数列{}n b 的前n 项和n T . 3．设等比数列{}n a 的前n 项和为n S ，，2S ，3S 成等差数列，数列{}n b 满足2n b n =．（1）求数列{}n a 的通项公式；（2）设n n n c a b =?，若对任意*n N ∈，求λ的取值范围． 4．已知等差数列{n a }的公差2d =，其前n 项和为n S ，且等比数列{n b }满足11b a =， 24b a =，313b a =．（Ⅰ）求数列{n a }的通项公式和数列{n b }的前n 项和n B ；（Ⅱ）记数列的前n 项和为n T ，求n T ． 5．设数列{}n a 的前n 项和为n S ，且满足()21,2,3,n n S a n =-=．（1）求数列{}n a 的通项公式；（2）若数列{}n b 满足11b =，且1n n n b b a +=+，求数列{}n b 的通项公式；（3）设()3n n c n b =-，求数列{}n c 的前n 项和n T ．

高中数学全国卷数列专题复习

数列专题复习（1）一、等差数列和等比数列的性质 1、已知{}n a 是公差为1的等差数列，n S 为{}n a 的前n 项和，若844S S =，则10a = （A ） 172 （B ）19 2 （C ）10 （D ）12 2、数列{}n a 中112,2,n n n a a a S +==为{}n a 的前n 项和，若126n S =，则n = 3、设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S = A 5 B 7 C 9 D 11 4、已知等比数列{}n a 满足114a =,()35441a a a =-,则2a = A.2 B.1 1C.2 1 D. 8 5、等比数列｛a n ｝满足a 1=3， 135a a a ++ =21，则357a a a ++= A21 B42 C63 D84 6、等差数列{}n a 的公差为2，若2a ，4a ，8a 成等比数列，则{}n a 的前n 项和n S = （A ） ()1n n + （B ）()1n n - （C ） ()12 n n + (D) ()12 n n - 7、设等差数列{a n }的前n 项和为S n ，若S m －1＝－2，S m ＝0，S m ＋1＝3，则m ＝ A ．3 B ．4 C ．5 D ．6 8、等比数列｛a n ｝的前n 项和为S n ，已知S 3 = a 2 +10a 1 ，a 5 = 9，则a 1= （A ） 13 （B ）13 - （C ） 19 （D ）1 9 - 9、已知{n a }为等比数列，472a a +=，568a a =-，则110a a += A7 B5 C －5 D －7 10、已知各项均为正数的等比数列{n a }，123a a a =5，789a a a =10，则456a a a = (A) 11、如果等差数列{}n a 中，34512a a a ++=，那么127...a a a +++= （A ）14 （B ）21 （C ）28 （D ）35 12、等差数列{a n }的前n 项和为S n ，已知S 10=0，S 15 =25，则nS n 的最小值为________. 13、等比数列{}n a 的前n 项和为n S ，若3230S S +=，则公比q =___________。 14、设S n 为等差数列{}n a 的前n 项和，若a 1=1，公差d =2，S k +2-S k =24，则k = (A)8 (B)7 (C) 6 (D) 5 15、设△A n B n C n 的三边长分别为a n ，b n ，c n ，△A n B n C n 的面积为S n ，n ＝1,2,3，….若b 1＞c 1， b 1＋ c 1＝2a 1，a n ＋1＝a n ，b n ＋1＝ 2n n c a +，c n ＋1＝2 n n b a +，则( )．

高中数学讲义微专题55 数列中的不等关系

第55炼数列中的不等关系一、基础知识： 1、在数列中涉及到的不等关系通常与数列的最值有关，而要求的数列中的最值项，要依靠数列的单调性，所以判断数列的单调性往往是此类问题的入手点 2、如何判断数列的单调性：（1）函数角度：从通项公式入手，将其视为关于n 的函数，然后通过函数的单调性来判断数列的单调性。由于n N * ∈ ，所以如果需要用到导数，首先要构造一个与通项公式形式相同，但定义域为()0,+∞ 的函数，得到函数的单调性后再结合n N * ∈得到数列的单调性（2）相邻项比较：在通项公式不便于直接分析单调性时，可考虑进行相邻项的比较得出数列的单调性，通常的手段就是作差（与0比较，从而转化为判断符号问题）或作商（与1比较，但要求是正项数列） 3、用数列的眼光去看待有特征的一列数：在解数列题目时，不要狭隘的认为只有题目中的 {}{},n n a b 是数列，实质上只要是有规律的一排数，都可以视为数列，都可以运用数列的知识来进行处理。比如：含n 的表达式就可以看作是一个数列的通项公式；某数列的前n 项和n S 也可看做数列{}12:,,,n n S S S S L 等等。 4、对于某数列的前n 项和{}12:,,,n n S S S S L ，在判断其单调性时可以考虑从解析式出发，用函数的观点解决。也可以考虑相邻项比较。在相邻项比较的过程中可发现：1n n n a S S -=-，所以{}n S 的增减由所加项n a 的符号确定。进而把问题转化成为判断n a 的符号问题二、典型例题例1：已知数列{}1,1n a a =，前n 项和n S 满足()130n n nS n S +-+= （1）求{}n a 的通项公式（2）设2n n n n c a λ?? =- ??? ，若数列{}n c 是单调递减数列，求实数λ的取值范围解：（1）()113 30n n n n S n nS n S S n +++-+=? =