
高三文科数学总复习
集合:
1、集合元素的特征:①确定性 ②互异性 ③无序性
2、常用数集及其记法:①自然数集(或非负整数集)记为N 正整数集记为*
N 或+N ②整数集记为Z ③实数集记为R ④有理数集记为Q 3、重要的等价关系:B A B B A A B A ??=?=
4、一个由n 个元素组成的集合有n
2个不同的子集,其中有12-n 个非空子集,也有12-n 个真子集
函数:
1、函数单调性
(1)证明:取值--—作差----变形----定号----结论 (2)常用结论:
①若()f x 为增(减)函数,则()f x -为减(增)函数 ②增+增=增,减+减=减
③复合函数的单调性是“同增异减”
④奇函数在对称区间上的单调性相同,偶函数在对称区间上的单调性相反
9、函数奇偶性
(1)定义:①)()(x f x f =-, )(x f 就叫做偶函数 ②)()(x f x f -=-, )(x f 就叫做奇函数 注意:①函数为奇偶函数的前提是定义域在数轴上关于原点对称 ②奇函数的图像关于原点对称,偶函数的图象关于y 轴对称
③若奇函数)(x f 在0=x 处有意义,则0)0(=f (2)函数奇偶性的常用结论:
奇 + 奇 = 奇,偶 + 偶 = 偶,奇 * 奇 = 偶,偶 * 偶 = 偶,奇 * 偶 = 奇
基本初等函数
1、(1)一般地,如果a x n
=,那么x 叫做a 的n 次方根。其中+∈>N n n ,1
①负数没有偶次方根 ②0的任何次方根都是0,记作00=n
③当n 是奇数时,a a n n =,当n 是偶数时,?
??<≥-==)0()0(||a a a a a a n
n
④我们规定:(1)m n m n
a a =()
1,,,0*>∈>m N n m a (2)()01>=-n a
a n n
(2)对数的定义:若N a b
=,那么N b a log =,其中a 叫做对数的底数, b 称为以a 为底的N 的对数,N
叫做真数
注:(1)负数和零没有对数(因为0>=b
a N ) (2)1log ,01log ==a a a (0>a 且1≠a )
(3)将N b a log =代回N a b
=得到一个常用公式log a N
a
N = (4)x N N a a x
=?=log
2、(1)①()Q s r a a
a a s
r s
r
∈>=+,,0②()()Q s r a a a rs s
r ∈>=,,0 ③()()Q r b a b a ab r r r
∈>>=,0,0
(2)①()N M MN a a a log log log += ②N M N M a a a log log log -=??
? ?? ③M n M a n
a log log =
④换底公式:a
b
b c c a log log log = ()0,1,0,1,0>≠>≠>b c c a a ,利用换底公式推导下面的结论:
(1)b m
n
b a n
a m
log log
=
(2)a b b a log 1log =
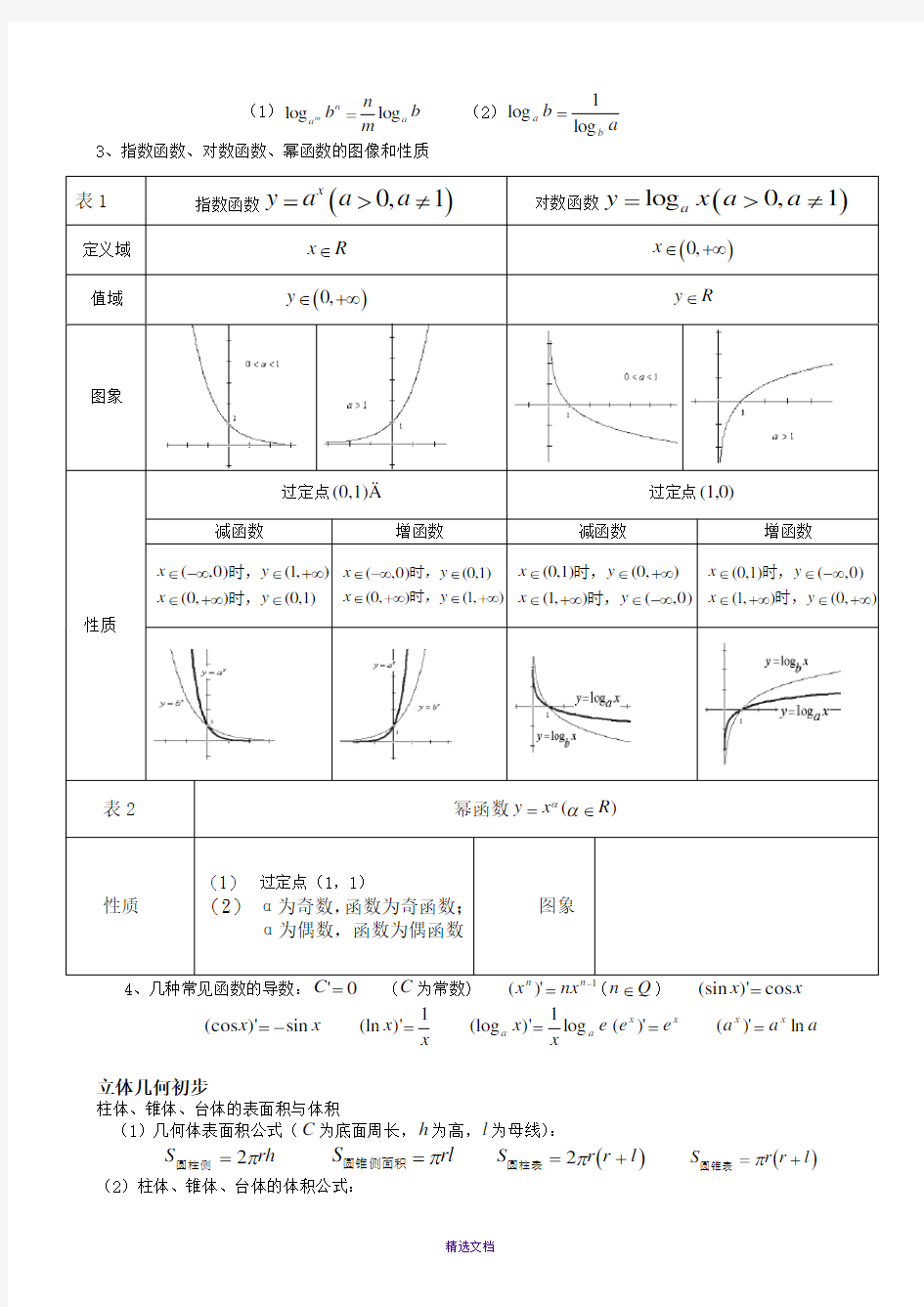
3、指数函数、对数函数、幂函数的图像和性质
4、几种常见函数的导数:0'=C (C 为常数) )'(=nx
x (Q n ∈) x x cos )'(sin =
x x sin )'(cos -= x x 1)'(ln =
e x
x a a log 1)'(log =x x e e =)'( a a a x
x ln )'(=
立体几何初步
柱体、锥体、台体的表面积与体积
(1)几何体表面积公式(C 为底面周长,h 为高,l 为母线): rh S π2=圆柱侧 rl
S π=圆锥侧面积 ()l r r S +=π2圆柱表 ()l r r S +=π圆锥表
(2)柱体、锥体、台体的体积公式:
表1
指数函数
()0,1x y a a a =>≠
对数函数
()log 0,1a y x a a =>≠
定义域 x R ∈ ()0,x ∈+∞
值域
()0,y ∈+∞
y R ∈
图象
性质
过定点(0,1)
过定点(1,0)
减函数
增函数 减函数 增函数
(,0)(1,)(0,)(0,1)
x y x y ∈-∞∈+∞∈+∞∈时,时, (,0)(0,1)(0,)(1,)x y x y ∈-∞∈∈+∞∈+∞时,时, (0,1)(0,)(1,)(,0)x y x y ∈∈+∞∈+∞∈-∞时,时,
(0,1)(,0)
(1,)(0,)x y x y ∈∈-∞∈+∞∈+∞时,时,
表2
幂函数()y x R αα=∈
性质
(1) 过定点(1,1)
(2) α为奇数,函数为奇函数;
α为偶数,函数为偶函数
图象
V Sh =柱 2V Sh r h π==圆柱 1
3V Sh =锥 h r V 23
1π=圆锥
(3)球体的表面积和体积公式:3
R 3
4π=
球V 2R 4S π=球面 直线与方程
1、直线的斜率
过两点的直线的斜率公式:)(211
21
2x x x x y y k ≠--=
2、直线方程
①点斜式:)(11x x k y y -=-直线斜率k ,且过点()11,y x
②斜截式:b kx y +=,直线斜率为k ,直线在y 轴上的截距为b
③两点式:11
2121
y y x x y y x x --=
--(1212,x x y y ≠≠)直线两点()11,y x ,()22,y x ④截矩式:
1x y
a b
+=,其中直线与x 轴、y 轴的截距分别为,a b ⑤一般式:0=++C By Ax (B A ,不全为0) 3、两直线平行与垂直
212121,//b b k k l l ≠=?;12121-=?⊥k k l l
4、两点间距离公式:
||AB = 5、点到直线距离公式: 2
200B A C By Ax d +++=
6、两平行直线距离公式:2
2
21B
A C C d +-=
圆的方程
1、圆的方程
(1)标准方程()()2
2
2
r b y a x =-+-,圆心
()b a ,,半径为r
(2)一般方程02
2=++++F Ey Dx y x 2、直线与圆的位置关系:
直线与圆的位置关系有相离,相切,相交三种情况,判断方法:
设直线0:=++C By Ax l ,圆()()222:r b y a x C =-+-,圆心()b a C ,到l 的距离为
2
2B A C Bb Aa d +++=,则有相离与C l r d ?>;相切与C l r d ?=;相交与C l r d ?<
3、圆与圆的位置关系:通过两圆半径的和(差),与圆心距(d )之间的大小比较来确定
设圆()()221211:r b y a x C =-+-,()()22
2222:R b y a x C =-+- 当r R d +>时 ,两圆外离 当r R d +=时 ,两圆外切
当r R d r R +<<-时 ,两圆相交 当r R d -=时,两圆内切
当r R d -<时,两圆内含 当0=d
时,为同心圆
三角函数
1、与角α终边相同的角的集合为{}
360,k k ββα=?+∈Z
2、设α是一个任意大小的角,α的终边上任意一点P 的坐标是(),x y ,它与原点的距离是 (
)
220r r x y =
+>,则sin y r α=
,cos x r α=,()tan 0y
x x
α=≠ 3、三角函数在各象限的符号:一全正,二正弦,三余弦,四正切 4、同角三角函数的基本关系:()221sin cos 1αα+= ()
sin 2tan cos α
αα
= 5、三角函数的诱导公式:推导口诀:奇变偶不变,符号看象限
()()1sin 2sin k παα+=,()cos 2cos k παα+=,()()tan 2tan k k παα+=∈Z ()()2sin sin παα+=-,()cos cos παα+=-,()tan tan παα+= ()()3sin sin αα-=-,()cos cos αα-=,()tan tan αα-=- ()()4sin sin παα-=,()cos cos παα-=-,()tan tan παα-=- ()5sin cos 2παα??-=
???,cos sin 2παα??-= ??? ()6sin cos 2παα??+= ???,cos sin 2παα??
+=- ???
sin y x =
cos y x = tan y x =
图象
定义域 R R
,2x x k k ππ??
≠+∈Z ????
值域
[]1,1-
[]1,1-
R
最值
当22
x k π
π=+
,max 1y =; 当22x k π
π=-
,min 1y =- 当x=2k π时,max 1y =;
当2x k ππ=+,min 1y =-.
既无最大值也无最小值
周期性
2π 2π π 奇偶性
奇函数
偶函数
奇函数
单调性
2,222k k ππππ??-+????
上增;32,222k k ππππ??++???
?上减 []()2,2k k k πππ-∈Z 上增;在[]2,2k k πππ+上减
在,22k k ππππ?
?-+ ??
?上增
对称性
对称中心()(),0k k π∈Z
对称轴()2
x k k ππ=+∈Z 对称中心(),02k k π
π??
+∈Z ???
对称中心(),02k k π??
∈Z
???
无对称轴
函
数 性 质
对称轴()x k k π=∈Z
有2sin sin sin a b c
R C ===A B 8、余弦定理:2222cos a b c bc =+-A ,2222cos b a c ac =+-B ,222
2cos c a b ab C =+-
推论:222cos 2b c a bc +-A = 222cos 2a c b ac +-B = 222
cos 2a b c C ab
+-=
9、三角形面积公式:111
sin sin sin 222
C S bc ab C ac ?AB =A ==B
平面向量
1、向量加法运算:
⑴三角形法则的特点:首尾相连,首指尾 ⑵平行四边形法则的特点:首首相连,对角线
(3)坐标运算:设()11,a x y =,()22,b x y =,则()1212,a b x x y y +=++ 2、向量减法运算:
⑴三角形法则的特点:首首相连,指被减
⑵坐标运算:设()11,a x y =,()22,b x y =,则()1212,a b x x y y -=-- 3、向量数乘运算:
⑴实数λ与向量a 的积是一个向量的运算叫做向量的数乘,记作a λ
①
a a λλ=
②当0λ>时,a λ的方向与a 的方向相同;
当0λ<时,a λ的方向与a 的方向相反; 当0λ=时,0a λ=
(2)坐标运算:设(),a x y =,则()(),,a x y x y λλλλ==
4、向量共线定理:向量()
0a a ≠与b 共线,当且仅当有唯一一个实数λ,使b a λ=
设()11,a x y =,()22,b x y =,其中0b ≠,则当且仅当12210x y x y -=时,向量a 、()
0b b ≠共线 5、平面向量的数量积:
⑴()
cos 0,0,0180a b a b a b θθ?=≠≠≤≤.零向量与任一向量的数量积为0
⑵性质:设a 和b 都是非零向量,则①0a b a b ⊥??= ②当a 与b 同向时,a b a b ?= 当a 与b 反向时,a b a b ?=- 2
2
a a a a ?==或a a a =? ③a
b a b ?≤ ⑶坐标运算:设两个非零向量()11,a x y =,()22,b x y =,则1212a b x x y y ?=+ 若(),a x y =,则2
2
2
a x y =+,或22a x y =
+
12120a b x x y y ⊥?+=
121222221
1
22
cos a b a b
x y
x y
θ?=
=
++
24、两角和与差的正弦、余弦和正切公式:
⑴()cos cos cos sin sin αβαβαβ-=+ ⑵()cos cos cos sin sin αβαβαβ+=-
b
a
C B
A
a b C C
-=A -AB =B
⑶()sin sin cos cos sin αβαβαβ-=- ⑷()sin sin cos cos sin αβαβαβ
+=+
⑸()tan tan tan 1tan tan αβ
αβαβ--=
+(()()tan tan tan 1tan tan αβαβαβ-=-+)
(6)()tan tan tan 1tan tan αβ
αβαβ
++=-(()()tan tan tan 1tan tan αβαβαβ+=+-)
25、二倍角的正弦、余弦和正切公式: ⑴sin22sin cos ααα= ⑵2
222cos2cos sin 2cos 112sin ααααα=-=-=-(2cos 21cos 2αα+=
,2
1cos 2sin 2
αα-=) ⑶22tan tan 21tan α
αα
=
-
26、辅助角公式:)sin(cos sin 22?ααα++=
+b a b a ,其中a
b =
?tan 数列
1、等差数列: ()11n
a a n d =+-
性质:等差中项:若a 、b 、c 成等差,则2b=a+c
若m n p q +=+(m 、n 、p 、*
q ∈N ),则q p n m a a a a +=+; 若2n p q =+(n 、p 、*q ∈N ),则q p n a a a +=2
前n 项和的公式:①2
)
(1n n a a n S += ②()1
12n n n S na d -=+ 2、等比数列:11n n a a q -=
性质:等比中项:若a ,G ,b 成等比数列,则2
G ab =
若m n p q +=+,则m n p q a a a a ?=?;
若2n p q =+,则q p n a a a ?=2
前n 项和的公式:()()()11111111n n n na q S a q a a q q q
q =??
=-?-=≠?
--?
3、和项关系: ???≥-==-2111
n S S n S a n n
n
4、数列求和的方法:(1)套用公式法: ①等差数列求和公式:()()
11122n n n a a n n S na d +-=
=+ ②等比数列求和公式:()()()11111111n n n na q S a q a a q q q
q ?=?
=-?-=≠?
--?
(2)裂项相消法:
()1111n n k k n n k ??
=- ?++??
(3)分组求和法:等差+等比 (4)错位相减法:等差*等比 (5)倒序相加法
不等式
基本不等式: 若0a >,0b >,则2a b ab +≥,即
2
a b
ab +≥ 变形 ①()2
2
2,a b ab a b R +≥∈ ②()2
0,02a b ab a b +??
≤>> ???
圆锥曲线
1、椭圆:平面内与两个定点1F ,2F 的距离之和等于常数(大于12
F F )的点的轨迹称为椭圆 即:|)|2(,2||||2121F F a a MF MF >=+,这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距 几何性质: 焦点的位置
焦点在x 轴上
焦点在y 轴上
图形
标准方程 ()22
2210x y a b a b +=>> ()22
2210y x a b a b
+=>> 轴长
短轴的长2b = 长轴的长2a =
顶点
()1,0a A -、()2,0a A
()10,b B -、()20,b B
焦点 ()1,0F c -、()2,0F c ()10,F c -、()20,F c
焦距 ()222122F F c c a b ==-
对称性 关于x 轴、y 轴、原点对称
离心率
()2
2101c b e e a a
==-<<
2、双曲线:平面内与两个定点1F ,2F 的距离之差的绝对值等于常数(小于12F F )的点的轨迹
即:
|)|2(,2||||||2121F F a a MF MF <=-这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距焦点的位置
焦点在x 轴上
焦点在y 轴上
图形
标准方程
()22
2210,0x y a b a b -=>> ()22
2
210,0y x a b a b
-=>> 顶点 ()1,0a A -、()2,0a A ()10,a A -、()20,a A 焦点 ()1,0F c -、()2,0F c
()10,F c -、()20,F c
焦距 ()222122F F c c a b ==+
对称性 关于x 轴、y 轴对称,关于原点中心对称
离心率
()2
211c b e e a a
==+>
渐近线方程 b y x a
=±
a y x b
=±
3、抛物线:平面内与一个定点和一条定直线的距离相等的点的轨迹.定点称为抛物线的焦点,定直线l 称为抛物线的准线
几何性质:()0p > 标准方程
22y px = 22y px =- 22x py = 22x py =-
图形
顶点 ()0,0
对称轴 x 轴
y 轴
焦点
,02p F ??
??? ,02p F ??
- ???
0,2p F ?
? ??
?
0,2p F ?
?- ??
?
准线方程 2
p
x =-
2
p x =
2
p y =-
2
p y =
离心率
1e =
(注:可编辑下载,若有不当之处,请指正,谢谢!)