
Mac
上页下页返回
首页回顾: 三重积分的计算
1.利用直角坐标计算三重积分
——将三重积分化为三次积分.
方法1 . 投影法(“先一后二”)
方法2 . 截面法(切片法) (“先二后一”)
Mac
上页下页返回
首页【方法1】:投影法【“先一后二”】如图
xy
D xoy 面投影为平面闭区域向将空间闭区域Ω )1(),
,(:),,(:2211y x z z S y x z z S ==轴,
作直线过点z D y x xy //),()2(∈.穿出,从穿入从ΩΩ21z z x
y
z
o
Ω
xy
D a b
)
(1x y y =)
(2x y y =)
,(1y x z z =)
,(2y x z z =),(y x 1
z 2
z Mac
上页下页返回
首页
?
=)
,()
,(21),,(),(y x z y x z dz
z y x f y x F 上的二重积分
在闭区域计算xy D y x F ),( )4(.
]),,([),()
,()
,(21
?????=xy
xy
D y x z y x z D d dz z y x f d y x F σσ),()( , :21x y y x y b x a D xy ≤≤≤≤ 得
.
的函数、为y x X—型域的函数,看作将看作定值先将z z y x f y x ),,(,,)3(=
???
Ω
dv z y x f ),,(.
),,()()
()
,(),(2121??
?
b
a
x y x y y x z y x z dz z y x f dy dx Mac
上页下页返回
首页注意:
.
交点的边界曲面与闭区域内部的直线
轴且穿过闭区域要求平行于2≤ΩΩS z 右式称为先对z 、次对y 、最后对x 的三次积分
(1)=
???
Ω
dv z y x f ),,(.
),,()()()
,()
,(21
21
???b a x y x y y x z y x z dz z y x f dy dx (2)若交点多于两个,可将Ω分割为若干小区域,再求和.(3)也可把Ω投影到yoz 面或zox 面上,便可
把三重积分化为其它顺序的三次积分.
(平行x 轴或y 轴,穿过Ω内的直线与Ω的边界交点≦2).
补例3
Mac
上页
下页
返回
首页
例1:.
12
所围成的闭区域及平面为三个坐标面,其中计算=++Ω???Ω
z y x xdxdydz 解:
x
y
z
o
)
0,0,1(A )0,2
1,
0(B )
1,0,0(C xy
D 如图OAB
D xoy xy 为闭域面得投影到将Ω?????-≤≤≤≤)
1(2
1010x y x D xy :X—型域
故
?
?
?
??--≤≤-≤≤≤≤Ωy x z x y x 210)
1(2101
0:则
?
?
????---Ω
=y
x x xdz
dy dx xdxdydz 210
)1(21
1
0Mac
上页下页返回
首页 (1) 把积分区域Ω向某轴(例如z 轴)投影,得
投影区间],[21c c ;
(3)计算二重积分??z
D dxdy z y x f ),,(
其结果为z 的函数)(z F ;
z
【方法Ⅱ】截面法(切片法)【“先二后一”】
(2) 对],[21c c z ∈用过z 点且平行xoy 平面的平面去
截Ω,得截面z D ;
(4)最后计算单积分?2
1
)(c c dz z F 即得三重积分值.
Mac
上页
下页
返回
首页
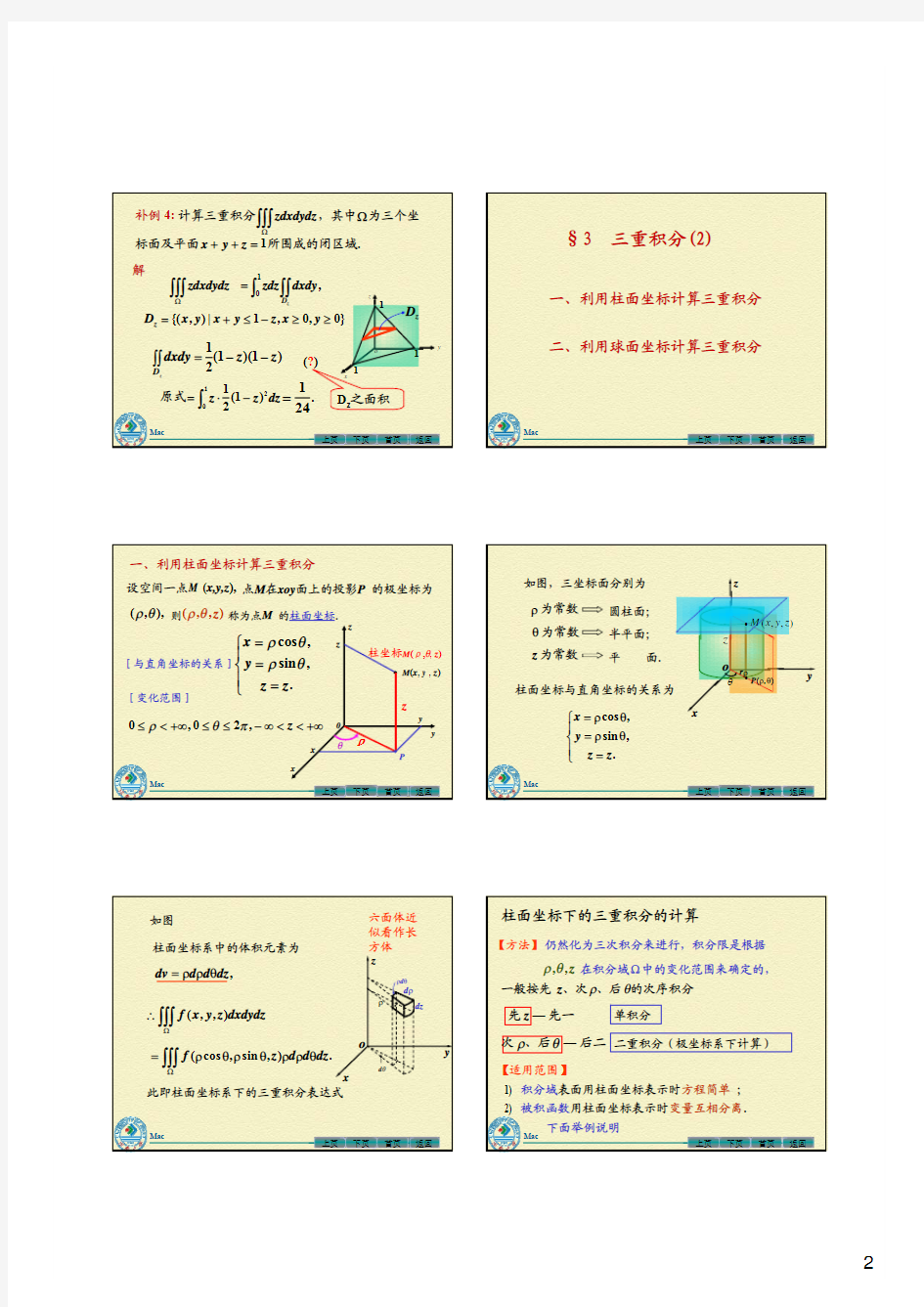
补例4: 计算三重积分???Ω
zdxdydz ,其中Ω为三个坐
标面及平面1=++z y x 所围成的闭区域.
解
???Ω
zdxdydz ,
1
???=z
D dxdy zdz }
0,0,1|),{(≥≥-≤+=y x z y x y x D z )1)(1(21
z z dxdy z
D
--=??原式?
-?=
1
02)1(21
dz z z 24
1=. x
o
z
y
1
1
1
(?)
z
D D z 之面积
Mac
上页下页返回
首页§3 三重积分(2)
一、利用柱面坐标计算三重积分二、利用球面坐标计算三重积分
Mac
上页下页返回首页??
?
??===.,
sin ,
cos z z y x θρθρ设空间一点M (x,y,z ),),,(θρ则称为点M 的柱面坐标.
),,(z θρ[变化范围]
[与直角坐标的关系]0
x
z
y
M (x , y , z )
z
θ
ρ
P
x
y
z
,20 ,0+∞<<∞-≤≤+∞<≤z πθρ一、利用柱面坐标计算三重积分
柱坐标M (ρ,θ, z )
点M 在xoy 面上的投影P 的极坐标为
Mac
上页下页返回
首页??
?
??=θρ=θρ=.,sin ,cos z z y x 柱面坐标与直角坐标的关系为
为常数
ρ为常数
z 为常数
θ如图,三坐标面分别为
圆柱面;半平面;平
面.
?
)
,,(z y x M )
,(θρP ?
θ
ρ
r z
x
y
z
o
Mac
上页下页返回
首页???Ω
∴dxdydz
z y x f ),,(.
),sin ,cos (???Ω
θρρθρθρ=dz d d z f θ
d ρ
x
y
z
o
dz
ρ
d θ
ρd 柱面坐标系中的体积元素为
,
dz d d dv θρρ=此即柱面坐标系下的三重积分表达式
如图
六面体近似看作长方体
Mac
上页
下页
返回
首页
柱面坐标下的三重积分的计算
仍然化为三次积分来进行,积分限是根据
z ,,θρ在积分域Ω中的变化范围来确定的,
下面举例说明
的次序积分
、后、次一般按先θρz 先一
先—z 后二、后次—θρ单积分
二重积分(极坐标系下计算)【方法】【适用范围】
1) 积分域表面用柱面坐标表示时方程简单;2) 被积函数用柱面坐标表示时变量互相分离.
Mac
上页
下页
返回
首页
z y x y x I d d d 1
1
?
22
???
++=
所围锥面 1 , :222==+Ωz z y x 0
x
z
y
1
D xy
z
I D
d 1
1
d d 1 2???+=ρρθρρ??
?
+=1
1
22 0
d d 1d ρπρρρ
θz
)2
22(ln π
π+-=.:ΩD xy :ρ
=z
10,20≤≤
≤≤ρπθz = 1
锥面化为:ρ= z
1.:下底:上顶用柱面坐标例1:?-++=102
)d 111(2ρ
ρρπ..
解:
??
?
??=θρ=θρ=.,sin ,cos z z y x Mac
上页
下页
返回
首页
x
z y
4
D xy
2例2:
利用柱面坐标计算三重积分???Ω
zdxdydz
所围闭域
与平面是由曲面其中422=+=Ωz y x z 解:
:D xoy 面得投影到将Ω4
:22≤+y x D 即
2
0,20:≤≤≤≤ρπθD )
,(θρ内任取一点在D 轴平行的直线作与z 外
穿出从平面内,
穿入从曲面Ω=Ω+=422z y x z Mac
上页下页
返回
首页
??
?
??≤≤≤≤≤≤Ω42
020:2z ρρπθ则故
???=4
20
20
2ρ
πρρθzdz
d d ??-=20420
)16(21ρ
ρρθπ
d d π
ρρπ3
64]618[2
062=-=【思考】本题是否可考虑用截面法来求解?
??????Ω
Ω
=dz
d d z zdxdydz θρρMac
上页
下页
返回
首页
例3:
. 0)(,
222所围与
由其中计算三重积分=--=Ω=
???Ω
z y x R z zdv I x
y
z
解:
π
θρ20 ,0:)(≤≤≤≤ΩR D xoy xy 为圆面投影向)
(xy D ??xy
D [?
-2
20
ρρR dz z ?
?-=
R
d R d 0
2220
)(21ρρρθπ
0 22ρ-≤
≤R z 此时.4
1
4R π=【思考】是否也可考虑用截面法来求解?
?
?
θ
ρd d ]=∴I Mac
上页下页返回
首页0
x z
y
1
D xy 3解:由 ??
?
??===z
z y x θρθ
ρsin cos ,
??
?==+z
z 34
2
22ρρ,
3,1==?ρz 知交线为????
???≤≤≤≤-≤≤Ω .20 ,3043:22πθρρρ,
z ???-?=2
2432030ρρπ
ρρθzdz d d I .
413
π=例4:计算???Ω
=zdxdydz I ,其中Ω是球面
42
22=++z y x 与抛物面z y x 322=+
所围的立体.
Mac
上页下页返回
首页
Mac
上页下页返回
首页的球面坐标.
就叫做点,
,个数面上的投影,这样的三在点为的角,这里段逆时针方向转到有向线轴按轴来看自为从正轴正向所夹的角,与为有向线段间的距离,与点点为原来确定,其中,,三个有次序的数可用为空间内一点,则点设M r xoy M P OP x z z OM M O r r M z y x M θ?θ?θ?),,(二、利用球面坐标计算三重积分
Mac
上页下页返回
首页0
x
z
y
M (r ,?, θ)
r
θ
?
P
y
x
z
=x =y =z θ?cos sin r θ?sin sin r ?
cos r 球面坐标????
? ??≤≤≤≤+∞<≤π0π200?θr )
,,(θ?r Mac
上页
下页
返回
首页
为常数
?圆锥面;
为常数
r 球面;
为常数
θ半平面.
?
r
x
z
y
θ
Mac
上页下页返回
首页???Ω=
dxdydz z y x f ),,(???Ω
.
sin )cos ,sin sin ,cos sin (2
θ???θ?θ?d drd r
r r r f 球面坐标系中的体积元素为
,
sin 2
θ??d drd r dv =θ
d r
x
y
z
o
dr
θ
?d sin r ?
rd ?
d ?
θ
θ
d ?
sin r 如图,
此即球面坐标下三重积分表达式
六面体近似看作长方体
Mac
上页
下页
返回
首页
注:
(1))
,(θ?r r =Ω其边界曲面方程为域,
是包围原点在内的闭区若则???Ω
=θ
??θ?d drd r r F I sin ),,(2?
???=)
,(0
20
20
sin θ?ππ??θr dr
r F d d 球面坐标下的三重积分的计算
.
的三次积分进行计算、最后对、次对一般按照化为先对θ?r ,r +∞<≤0.
20πθ≤≤,
0π?≤≤规定:
Mac
上页下页返回
首页(3)
)2(1),,(即得球的体积时,由当≡z y x f
3
4
sin 302020a dr r d d V a π??θππ===??? (2)围成时
由球面当a r =Ω ????=a
dr
r F d d I 0
20
20
sin ??θππ
其中)cos ,sin sin ,cos sin (),,(?θ?θ?θ?r r r f r F =
Mac 上页下页返回
首页
例5:.
所围立体的体积的内接锥面
的球面与半顶角为求半径为αa 解:如图建立坐标系
cos 2 ?a r =球面方程为 α?=锥面方程为???
??≤≤≤≤≤≤Ω?α
?πθcos 20020:a r x
o y
z
a
2α?r
M
则立体体积为???Ω
=z y x V d d d ??
cos 20
2d a r
r d sin cos 3
160
33
???πα
?=
a )
cos 1(3443
απ-=a ?α
?
?0
d sin ?=πθ
20
d r
r v d d d sin d 2?θ?=Mac
上页下页返回
首页z
y x d d d z
d d d θρρθ
??d d d sin 2
r r 积分区域多由坐标面被积函数形式简洁, 或坐标系体积元素适用情况直角坐标系柱面坐标系
球面坐标系变量可分离.
围成;
小
结
Mac
上页下页返回
首页作业
P164, 9(1);
10(1)11(1,2);
重积分的计算方法 重积分包括二重积分和三重积分,它是定积分的推广;被积函数由一元函数f(x)推广为二元函数f(x,y),三元函数(fx,y,z);积分围由数轴上的区域推广为平面域(二重积分)和空间域(三重积分)。我个人在学习与复习多重积分这一块时,感到多重积分的计算比较繁琐,而在日常生活中多重积分有着很多的应用。通过在图书馆查阅资料、以及老师的指点,重积分的计算方法还是有规律可循的。为了更好的应用重积分,本人结合前人的经验,在这里介绍几种常用的重积分计算方法,以及一些小技巧。着重介绍累次积分的计算与变量代换。 一.二重积分的计算 1.常用方法 (1)化累次积分计算法 对于常用方法我们先看两个例子
对于重积分的计算主要采用累次积分法,即把一个二重积分表达为一个二次积分,通过两次定积分的计算求得二重积分值,分析上面的例子累次积分法其主要步骤如下: 第一步:画出积分区域D的草图; 第二步:按区域D和被积函数的情况选择适当的积分次序,并确定积分的上、下限; 第三步:计算累次积分。 需要强调一点的是,累次积分要选择适当的积分次序。积分次序的不同将影响计算的繁简,有些题这两种次序的难易程度可以相差很大,甚至对一种次序可以“积出来”,而对另一种次序却“积不出来”。所以,适当选择积分次序是个很重要的工作。 选择积分次序的原则是:尽可能将区域少分块,以简化计算过程;第一次积分的上、下限表达式要简单,并且容易根据第一次积分的结果作第二次积分。 (2)变量替换法 着重看下面的例子:
在计算定积分时,求积的困难在于被积函数的原函数不易求得。从而适当地在计算重积分时,求积的困难来自两个方面,除了被积函数的原因以外还在而且,有时候其积分区域往往成为困难的主要方面。 利用换元法的好处是可以把被积函数的形状进行转化,以便于用基本求积公式。 于积分区域的多样性。为此,针对不同的区域要讨论重积分的各种不同算法。 (3)极坐标变换公式(主要是∫∫f(x,y)dxdy=∫∫f(pcosθ,psinθ)pdpdθ)
第一部分 定积分的计算 一、定积分的计算 例1 用定积分定义求极限. )0(21lim 1>++++∞→a n n a a a a n . 解 原式=?∑=??? ? ??=∞→1011lim a a n i n x n n i dx = a a x a += ++11 11 1. 例2 求极限 ? +∞→10 2 1lim x x n n dx . 解法1 由10≤≤x ,知n n x x x ≤+≤ 2 10,于是? +≤1 2 10x x n ?≤1 n x dx dx . 而?1 0n x ()∞→→+=+= +n n n x dx n 01111 01,由夹逼准则得?+∞→1021lim x x n n dx =0. 解法2 利用广义积分中值定理 ()()x g x f b a ? ()()?=b a x g f dx ξdx (其中()x g 在区间[]b a ,上不变号) , ().101111 2 1 02 ≤≤+= +? ? n n n n dx x dx x x ξξ 由于11102≤+≤ n ξ ,即 211n ξ +有界, ()∞→→+=?n n dx x n 0111 0,故?+∞→1021lim x x n n dx =0. 注 (1)当被积函数为( )22,x a x R +或() 22,a x x R -型可作相应变换. 如对积分() ?++3 1 2 2 112x x dx ,可设t x tan =; 对积分 ()0220 2>-? a dx x ax x a ,由于 () 2 222a x a x ax --=-,可设 t a a x s i n =-. 对积分dx e x ? --2 ln 0 21,可设.sin t e x =- (2)()0,cos sin cos sin 2 ≠++=?d c dt t d t c t b t a I π 的积分一般方法如下:
2016年专项练习题集-定积分的计算 一、选择题 1.dx x )5(1 22-?=( ) A.233 B. 31 C.3 4 D .83 【分值】5分 【答案】D 【易错点】求被积函数的原函数是求解关键。 【考查方向】求定积分 【解题思路】求出被积函数的原函数,应用微积分基本定理求解。 【解析】dx x )5(122-?=123153x x -=83 . 2.直线9y x =与曲线3 y x =在第一象限内围成的封闭图形的面积为( ) A 、 B 、 C 、2 D 、4 【分值】5分 【答案】D 【易错点】求曲线围成的图形的面积,可转化为函数在某个区间内的定积分来解决,被积函
数一般表示为曲边梯形上边界的函数减去下边界的函数. 【考查方向】定积分求曲线围成的图形的面积 【解题思路】先求出直线与曲线在第一象限的交点,再利用牛顿-莱布尼茨公式求出封闭图形的面积. 【解析】由? ??==39x y x y ,得交点为()()()27,3,27,3,0,0--, 所以()4 81034129942303 =??? ??-=-=?x x dx x x S ,故选D. 3.2 2-?2412x x -+dx =( ) A.π 4 B.π 2 C.π D.π3 【分值】5分 【答案】A 【易错点】利用定积分的几何意义,一般根据面积求定积分,这样可以避免求原函数,注意理解所涉及的几何曲线类型. 【考查方向】求定积分 【解题思路】利用定积分的几何意义,转化为圆的面积问题。 【解析】设y =2412x x -+,即(x -2)2+y 2=16(y ≥0).∵2 2-?2412x x -+dx 表示以4为半径的圆的四分之一面积.∴2 2-?2412x x -+dx =π4. 4.F4遥控赛车组织年度嘉年华活动,为了测试一款新赛车的性能,将新款赛车A 设定v =3t 2+1(m/s)的速度在一直线赛道上行驶,老款赛车B 设定在A 的正前方5 m 处,同时以v
第四节 三重积分及其计算和多重积分 在第三节中我们讨论了二重积分,本节将之推广到一般的n 维空间中去. 类似于第三节,我们先定义一个R 3中集合的可求体积性. 同样可以给出一列类似的结论. 读者自己推广. 这里将不再赘述. 一、 引例 设一个物体在空间R 3中占领了一个有界可求体积的区域V ,它的点密度为()z y x f ,,,现在要求这个物体的质量.假设密度函数是有界的连续函数,可以将区域V 分割为若干个可求体积的小区域n V V V ,...,,21,其体积分别是n V V V ???,...,,21,直径分别是n d d d ,...,,21,即},||sup{|i i V Q W WQ d ∈=, (i =1,2,…,n ), |WQ|表示W, Q 两点的距离.设 },...,,m ax {21n d d d =λ,则当λ很小时,()z y x f ,,在i V 上的变化也很小.可以用这个小 区域上的任意一点()i i i z y x ,,的密度()i i i z y x f ,,来近似整个小区域上的密度,这样我们可以求得这个小的立体的质量近似为()i i i i V z y x f ?,,,所有这样的小的立体的质量之和即为这个物体的质量的一个近似值.即 ()i i i i n i V z y x f M ?≈∑=,,1 . 当0→λ时,这个和式的极限存在,就是物体的质量.即 ()i i i i n i V z y x f M ?=∑=→,,lim 1 λ. 从上面的讨论可以看出,整个求质量的过程和求曲顶柱体的体积是类似的,都是先分割,再求和,最后取极限.所以我们也可以得到下面一类积分. 二、 三重积分的定义 设()z y x f ,,是空间3 R 中的一个有界可求体积的闭区域V 上的有界函数,将V 任意分割 为若干个可求体积的小闭区域n V V V ,...,,21,这个分割也称为V 的分划,记为P : n V V V ,...,,21. Φ=?o o j i V V (空, j i ≠), 其体积分别是n V V V ???,...,,21,直径分别是n d d d ,...,,21.设 },...,,m ax {21n d d d =λ,或记为||P ||. 在每个小区域中任意取一点()i i i i V z y x ∈,,,作和 ()i i i i n i V z y x f ?∑=,,1 (称为Riemann 和),若当0→λ时,这个和式的极限存在,则称其极
定积分典型例题 例1 求21lim n n →∞L . 分析 将这类问题转化为定积分主要是确定被积函数和积分上下限.若对题目中被积函数难以想到,可采取如下方法:先对区间[0,1]n 等分写出积分和,再与所求极限相比较来找出被积函数与积分上下限. 解 将区间[0,1]n 等分,则每个小区间长为1 i x n ?=,然后把2111n n n =?的一个因子1n 乘 入和式中各项.于是将所求极限转化为求定积分.即 21lim n n →∞+L =1lim n n →∞+L =34 =?. 例2 ? =_________. 解法1 由定积分的几何意义知,0 ?等于上半圆周22(1)1x y -+= (0y ≥) 与x 轴所围成的图形的面积.故0 ?= 2 π . 例18 计算2 1 ||x dx -?. 分析 被积函数含有绝对值符号,应先去掉绝对值符号然后再积分. 解 2 1||x dx -?=0 2 10()x dx xdx --+??=220210[][]22x x --+=5 2 . 注 在使用牛顿-莱布尼兹公式时,应保证被积函数在积分区间上满足可积条件.如 3 322 2111 []6 dx x x --=-=?,则是错误的.错误的原因则是由于被积函数21x 在0x =处间断且在被积区间内无界. 例19 计算2 20 max{,}x x dx ?. 分析 被积函数在积分区间上实际是分段函数 212()01x x f x x x ?<≤=?≤≤? . 解 232 12 2 2 12010 1 1717max{,}[][]23236 x x x x dx xdx x dx =+=+=+=? ?? 例20 设()f x 是连续函数,且10 ()3()f x x f t dt =+?,则()________f x =. 分析 本题只需要注意到定积分()b a f x dx ?是常数(,a b 为常数). 解 因()f x 连续,()f x 必可积,从而10 ()f t dt ?是常数,记1 ()f t dt a =?,则 ()3f x x a =+,且11 (3)()x a dx f t dt a +==??.
三重积分的计算方法介绍: 三重积分的计算是化为三次积分进行的。其实质是计算一个定积分(一重积分)和一个二重积分。从顺序看: 如果先做定积分?2 1),,(z z dz z y x f ,再做二重积分??D d y x F σ),(,就是“投 影法”,也即“先一后二”。步骤为:找Ω及在xoy 面投影域D 。多D 上一点(x,y )“穿线”确定z 的积分限,完成了“先一”这一步(定积分);进而按二重积分的计算步骤计算投影域D 上的二重积分,完成“后二”这一步。σd dz z y x f dv z y x f D z z ??????Ω =2 1]),,([),,( 如果先做二重积分??z D d z y x f σ),,(再做定积分?2 1 )(c c dz z F ,就是“截面 法”,也即“先二后一”。步骤为:确定Ω位于平面21c z c z ==与之间,即],[21c c z ∈,过z 作平行于xoy 面的平面截Ω,截面z D 。区域z D 的边界曲面都是z 的函数。计算区域z D 上的二重积分??z D d z y x f σ),,(,完成 了“先二”这一步(二重积分);进而计算定积分?2 1 )(c c dz z F ,完成“后 一”这一步。dz d z y x f dv z y x f c c D z ]),,([),,(2 1σ??????Ω = 当被积函数f (z )仅为z 的函数(与x,y 无关),且z D 的面积)(z σ容易求出时,“截面法”尤为方便。 为了简化积分的计算,还有如何选择适当的坐标系计算的问题。可以按以下几点考虑:将积分区域Ω投影到xoy 面,得投影区域D(平面) (1) D 是X 型或Y 型,可选择直角坐标系计算(当Ω的边界曲
三重积分的计算方法: 三重积分的计算是化为三次积分进行的。其实质是计算一个定积分(一重积分)和一个二重积分。从顺序看: 如果先做定积分?2 1),,(z z dz z y x f ,再做二重积分??D d y x F σ),(,就是“投 影法”,也即“先一后二”。步骤为:找Ω及在xoy 面投影域D 。多D 上一点(x,y )“穿线”确定z 的积分限,完成了“先一”这一步(定积分);进而按二重积分的计算步骤计算投影域D 上的二重积分,完成“后二”这一步。σd dz z y x f dv z y x f D z z ??????Ω =2 1]),,([),,( 如果先做二重积分??z D d z y x f σ),,(再做定积分?2 1 )(c c dz z F ,就是“截面 法”,也即“先二后一”。步骤为:确定Ω位于平面21c z c z ==与之间,即],[21c c z ∈,过z 作平行于xoy 面的平面截Ω,截面z D 。区域z D 的边界曲面都是z 的函数。计算区域z D 上的二重积分??z D d z y x f σ),,(,完成 了“先二”这一步(二重积分);进而计算定积分?2 1 )(c c dz z F ,完成“后 一”这一步。dz d z y x f dv z y x f c c D z ]),,([),,(2 1σ??????Ω = 当被积函数f (z )仅为z 的函数(与x,y 无关),且z D 的面积)(z σ容易求出时,“截面法”尤为方便。 为了简化积分的计算,还有如何选择适当的坐标系计算的问题。可以按以下几点考虑:将积分区域Ω投影到xoy 面,得投影区域D(平面) (1) D 是X 型或Y 型,可选择直角坐标系计算(当Ω的边界曲
定积分典型例题20例答案 例1 求33322 32 1lim (2)n n n n n →∞+++. 分析 将这类问题转化为定积分主要是确定被积函数和积分上下限.若对题目中被积函数难以想到,可采取如下方法:先对区间[0,1]n 等分写出积分和,再与所求极限相比较来找出被积函数与积分上下限. 解 将区间[0,1]n 等分,则每个小区间长为1i x n ?=,然后把2111n n n =?的一个因子1 n 乘 入和式中各项.于是将所求极限转化为求定积分.即 33322 32 1lim (2)n n n n n →∞+++=333 112 lim ()n n n n n n →∞++ +=1303 4 xdx =?. 例2 2 20 2x x dx -? =_________. 解法1 由定积分的几何意义知,2 20 2x x dx -?等于上半圆周22(1)1x y -+= (0y ≥) 与x 轴所围成的图形的面积.故220 2x x dx -? = 2 π . 解法2 本题也可直接用换元法求解.令1x -=sin t (2 2 t π π - ≤≤ ),则 2 2 2x x dx -? =2 2 2 1sin cos t tdt ππ- -? =2 2 21sin cos t tdt π -? =220 2cos tdt π ?= 2 π 例3 (1)若2 2 ()x t x f x e dt -=?,则()f x '=___;(2)若0 ()()x f x xf t dt =?,求()f x '=___. 分析 这是求变限函数导数的问题,利用下面的公式即可 () () ()[()]()[()]()v x u x d f t dt f v x v x f u x u x dx ''=-?. 解 (1)()f x '=42 2x x xe e ---; (2) 由于在被积函数中x 不是积分变量,故可提到积分号外即0()()x f x x f t dt =?,则 可得 ()f x '=0()()x f t dt xf x +?. 例4 设()f x 连续,且31 ()x f t dt x -=?,则(26)f =_________. 解 对等式310 ()x f t dt x -=? 两边关于x 求导得 32(1)31f x x -?=,
第二节 二重积分的计算法 教学目的:熟练掌握二重积分的计算方法 教学重点:利用直角坐标和极坐标计算二重积分 教学难点:化二重积分为二次积分的定限问题 教学内容: 利用二重积分的定义来计算二重积分显然是不实际的,二重积分的计算是通过两个定积分的计算(即二次积分)来实现的. 一、利用直角坐标计算二重积分 我们用几何观点来讨论二重积分的计算问题. 讨论中,我们假定 ; 假定积分区域可用不等式 表示, 其中, 在上连续. 据二重积分的几何意义可知,的值等于以为底,以曲面为顶的曲顶柱体的体积. 在区间上任意取定一个点,作平行于面的平面,这平面截曲顶柱体所得截面是一个以区间为底,曲线为曲边的曲边梯形,其面积为
一般地,过区间上任一点且平行于面的平面截曲顶柱体所得截面的面积为 利用计算平行截面面积为已知的立体之体积的方法,该曲顶柱体的体积为 从而有 (1) 上述积分叫做先对Y,后对X的二次积分,即先把看作常数,只看作的函数,对 计算从到的定积分,然后把所得的结果( 它是的函数 )再对从到计算定积分. 这个先对, 后对的二次积分也常记作 在上述讨论中,假定了,利用二重积分的几何意义,导出了二重积分的计算公式(1).但实际上,公式(1)并不受此条件限制,对一般的(在上连续),公式(1)总是成立的. 例如:计算 解: 类似地,如果积分区域可以用下述不等式 表示,且函数,在上连续,在上连续,则 (2)
显然,(2)式是先对,后对的二次积分. 二重积分化二次积分时应注意的问题 1、积分区域的形状 前面所画的两类积分区域的形状具有一个共同点: 对于I型(或II型)区域, 用平行于轴(轴 )的直线穿过区域内部,直线与区域的边界相交不多于两点. 如果积分区域不满足这一条件时,可对区域进行剖分,化归为I型(或II型)区域的并集. 2、积分限的确定 二重积分化二次积分, 确定两个定积分的限是关键.这里,我们介绍配置二 次积分限的方法 -- 几何法.画出积分区域的图形(假设的图形如下 ) 在上任取一点,过作平行于轴的直线,该直线穿过区域,与区域的边界有两个交 点与,这里的、就是将,看作常数而对积分时的下限和上限; 又因是在区间上任意取的,所以再将看作变量而对积分时,积分的下限为、上限为 . 例1计算,其中是由轴,轴和抛物线在第一象限内所围成的区域.
二、三重积分的计算技巧 重积分的计算中,对积分区域的熟悉非常重要,以下关于重积分的几种计算技巧均是基于积分区域的特点分析归纳得出。 一、积分区域为圆(二重积分)或球(三重积分) 1、 在闭区域D 为2 2 2 a y x ≤+的圆,区域关于原点,坐标轴均对称,则有 (1) dxdy y dxdy x a y x a y x ????≤+≤+= 2 222222 2 (2)若n m ,中有一个为奇数有 .02 22=??≤+dxdy y x a y x m n 例1.求 dxdy y x a y x ?? ≤++2 22)3(2 2 解:根据对称性, 原式=dxdy y x a y x ??≤++2 22)(2 2 2 =.24 200 3a dr r d a πθπ =?? 例2.求 dxdy y x a y x 2 2 22)3(??≤++ 解:原式= .2 5)(5)69(4 2 22 22 22222a dxdy y x dxdy xy y x a y x a y x π=+=++?? ?? ≤+≤+ 例3.求 .)53(2 2222 dxdydz z y x a z y x ??? ≤++++(积分区域为球) 解:原式= .)10306259(2 222222dxdydz xz yz xy z y x a z y x ??? ≤+++++++ = .32854.335.)(335552222 22 2a a dxdydz z y x a z y x ππ==++???≤++ 2、 在闭区域D 为2 2 2 )(a y a x ≤+-的圆上 例4.求 dxdy x a y a x ??≤+-2 22)( 解:原式= .)(3 2 )(2 22a dxdy a a x a y a x π=+-??≤+-
定积分的计算 班级 姓名 一、利用几何意义求下列定积分 (1)dx x ? 1 1 -2-1 (2)dx x ? 2 2-4 (3) dx x ? 2 2-2x (4) ()dx x x ? -2 4 二、定积分计算 (1)()dx ?1 7-2x (2)( ) d x ?+2 1 x 2x 32 (3)dx ?3 1 x 3 (4)dx x ?π π - sin (5)dx x ?e 1 ln (6)dx ? +1 x 112 (7)() dx x x ?+-10 2 32 (8)()dx 2 31 1-x ? (9)dx ?+1 1 -2x x 2)( (10)( ) d x x ?+21 2x 1x (11)() dx x x ?-+1 1 -352x (12)() dx e e x x ?+ln2 x -e (13)dx x ?+π π --cosx sin ) ( (14)dx ? e 1 x 2 (15)dx x ?2 1 -x sin -2e )( (16)dx ?++2 1-3x 1 x x 2 (17)dx ? 2 1x 13 (18)()dx 2 2 -1x ?+
三、定积分求面积、体积 1求由抛物线y 2=2x 与直线y =4-x 围成的平面图形的面积。 2.求曲线y =x ,y =2-x ,y =-1 3 x 所围成图形的面积. 3.求由曲线y =cos x (0≤x ≤2π)与直线y =1所围成的图形面积 4.如图求由两条曲线y =-x 2 ,y =-14 x 2 及直线y =-1所围成的图形的面积. 5、求函数f(x)=???? ? x +1 (-1≤x<0)cosx (0≤x ≤π 2)的图象与x 轴所围成的封闭图形的面积。 6.将由曲线y =x 2,y =x 3所 围成平面图形绕x 周旋转一周,求所得旋转体的体积。 7.将由三条直线x =0、x =2、y =0和曲线y =x 3所围成的图形绕x 周旋转一周,求所得旋转体的体积。 8.由曲线y =x 与直线x =1,x =4及x 轴所围成的封闭图形绕x 周旋转一周,求所得旋转体的体积
江西师范大学数学与信息科学学院 学士学位论文 三重积分的计算方法小结Methods of Calculation of Triple Integral 姓名:蒋晓颖 学号: 1007012048 学院:数学与信息科学学院 专业:数学与应用数学 指导老师:蒋新荣(副教授) 完成时间:2014年1月23日
三重积分的计算方法小结 蒋晓颖 【摘要】三重积分的计算是数学分析中的难点,本文结合教材以及相关资料较全面地给出了三重积分计算中的四种处理方法。第一,利用降低三重积分重数的思想,将其化为累次积分;第二,采用坐标变换的方法,将积分体表示成适当的形式;第三,充分运用被积函数的奇偶性和积分区域的对称性,简化计算;第四,利用高斯公式将三重积分的计算转化成曲面积分计算。希望这几种方法能对学习者具有一定的指导意义。 【关键词】三重积分累次积分坐标变换对称性高斯公式
Methods of Calculation of Triple Integral Jiang Xiaoying 【Abstract】The calculation of triple integral is the difficulty in Mathematics analysis.In this paper,unifying the teaching and related materials ,we give four instructive methods of the calculation of triple integral for learner.The four methods are as follows:the first,lower the multiplicity of triple integral and replace it with iterated integral;the second,with the method of coordinate alternate,we can transform the integral volume into appropriate form;the third,fully use the parity of integrand and symmetry of integral area to simplify calculation;finally,we can calculate the triple integral with the Gauss formula that could transform triple integral into a surface integral. 【Key words】triple integral iterated integral coordinate alternate symmetry Gauss formula
§5 三重积分 教学目的 掌握三重积分的定义和性质. 教学内容 三重积分的定义和性质;三重积分的积分换元法;柱面坐标变换;球面坐标变换. 基本要求 掌握三重积分的定义和性质,熟练掌握化三重积分为累次积分,及用柱面坐标变 换和球面坐标变换计算三重积分的方法. 教学建议 (1) 要求学生必须掌握三重积分的定义和性质,知道有界闭区域上的连续函数必可 积.由于三重积分的定义与性质及充要条件与二重积分类似,可作扼要叙述与比较. (2) 对较好学生可布置这节的广义极坐标的习题. 一、三重积分的概念 背景:求某非均匀密度的曲顶柱体的质量时,通过“分割、近似,求和、取极限”的步骤, 利用求柱体的质量方法来得到结果.一类大量的“非均匀”问题都采用类似的方法,从而归结出下面一类积分的定义. 定义1 设()z y x f ,,是定义在三维空间可求体积的有界闭区域V 上的函数,J 是一个确定的数,若对任给的正数ε,总存在某个正数δ,使对于V 的任何分割T ,当它的细度δ 则()z y x f ,,必在V 上可积. 二、化三重积分为累次积分 定理21.15 若函数()z y x f ,,在长方体V =[][][]f e d c b a ,,,??上的三重积分存在,且对任何x ∈[]b a ,,二重积分 ()x I =()dydz z y x f D ??,, 存在,其中D =[][]f e d c ,,?,则积分 ?b a dx ()??D d z y x f σ ,, 也存在,且 ()???V dxdydz z y x f ,,=?b a dx ()??D d z y x f σ ,,. (1) 为了方便有时也可采用其他的计算顺序.若简单区域V 由集合 ()()()()(){} b x a x y y x y y x z z y x z z y x V ≤≤≤≤≤≤=,,,,,,2121 所确定,V 在xy 平面上的投影区域为 D =()()(){ }b x a x y y x y y x ≤≤≤≤,,21 是一个x 型区域,设()z y x f ,,在上连续, ()y x z ,1,()y x z ,2在D 上连续,()x y 1,()x y 2上[]b a ,连续,则 ()???V dxdydz z y x f ,,= ()()???D z y x z dz z y x f dxdy 21,,,=()()()() ???b a x y x y z y x z dz z y x f dy dx 212 1,,,, 其他简单区域类似. 一般区域V 上的三重积分,常将区域分解为有限个简单区域上的积分的和来计算. 例1 计算 ???+V dxdydz y x 221 ,其中V 为由 第5章 定积分及其应用 (一)、单项选择题 1.函数()x f 在区间[a ,b]上连续是()x f 在[a ,b]上可积的( )。 A .必要条件 B 充分条件 C 充分必要条件 D 既非充分也非必要条件 2.下列等式不正确的是( )。 A . ()()x f dx x f dx d b a =??????? B. ()()()[]()x b x b f dt x f dx d x b a '=???? ??? C. ()()x f dx x f dx d x a =??????? D. ()()x F dt t F dx d x a '=???? ??'? 3.? ?→x x x tdt tdt sin lim 的值等于( ). A.-1 B.0 C.1 D.2 4.设x x x f +=3 )(,则 ? -2 2 )(dx x f 的值等于( )。 A .0 B.8 C. ? 2 )(dx x f D. ?2 )(2dx x f 5.设广义积分 ? +∞ 1 dx x α收敛,则必定有( )。 A.1-<α B. 1->α C. 1<α D. 1>α 6.求由1,2,===y x e y x 围成的曲边梯形的面积时,若选择x为积分变量,则积分区间为( )。 A.[0,2e ] B.[0,2] C.[1,2] D.[0,1] 7.由曲线2,0,===y x e y x 所围成的曲边梯形的面积为( )。 A.dy y ? 2 1 ln B. dy e e x ? 2 C.dy y ? 2 ln 1ln D. ()d x e x ?-2 1 2 8.由直线1,+-==x y x y ,及x轴围成平面图形的面积为( )。 A. ()[]dy y y ?--1 1 B. ()[]dx x x ? -+-21 1 C. ()[]dy y y ? --210 1 D.()[]dx x x ? +--1 1 9.由e x x y x y e ===,log ,ln 1围成曲边梯形,用微法求解时,若选x为积分变量,面积微元为 ( )。 A.dx x x e ???? ? ? +1 log ln B.dy x x e ???? ? ?+1log ln C.dx x x e ???? ? ?-1log ln D.dy x x e ??? ? ? ?-1log ln 10.由0,1,1,2==-==y x x x y 围成平面图形的面积为( )。 A. ? -1 1 2dx x B. ? 1 2dx x C. ? 1 dy y D.? 1 2 dy y 二重积分计算中积分限的确定 摘要:二重积分计算中积分限的确定对于初学者是一个重点更是一个难点.本文旨在介绍一种二重积分计算中确定积分限的简单易行的方法. 关键词:二重积分累次积分积分限积分次序 引言:高等数学学习过程中,二重积分计算是个难点。原因在于将二重积分化为累次积分时,对于积分限的确定学生难以掌握。本人结合自己的教学过程和自己的学习体会总结出一个口诀,发现在教学过程中效果不错可以很好的帮助学生解决这一难题。 1.高等数学中计算二重积分的方法 在高等数学课本中,在直角坐标系下计算二重积分的步骤为:]1[。 (1)画出积分区域 (2)确定积分区域是否为X-型或Y-型区域,如既不是X-型也不是Y-型区域,则要将 积分区域化成几个X-型和Y-型区域,并用不等式组表示每个X-型和Y-型区域. (3)用公式化二重积分为累次积分. (4)计算累次积分的值. 在教学的过程中我发现学生对于此种方法掌握的很不好,尤其是在第二步中,确定积分区域从而确定累次积分的积分限是一个薄弱环节.下面就本人在教学中的体会谈谈在这方面的一点心得. 2.教学过程中总结的方法 本人的心得可用下面的口诀概括:后积先定限,限内画条线,先交下限取,后交上限见.下面简单解释一下该口诀,然后以具体的例题加以说明.在将二重积分转化为累次积分的时候对于两个积分变量必然会有个先后顺序,这就要求对后积分的那个变量我们要根据积分区域确定其上下限(所谓确定是指根据积分区域图将其上下限定为常数).确定了这个变量的上下限以后,我们在其上下限内画一条和上下限平行的直线,该直线沿着坐标轴的正方向画过来,这样该直线如果和积分区域总是有两个交点,先交的即为另一个积分变量的积分下限,后交的即为其积分上限. 3.例题解析 例1 计算?? D xydxdy,其中D是由直线x y y x= = =,1 ,2所围成的区域. 解:作出积分区域D的图形 x 页脚内容1 题型 1.定积分与极限的计算 2.计算下列定积分 3.计算下列广义积分 内容 一.定积分的概念与性质 1.定积分的定义 2.定积分的性质 3.变上限函数及其导数 4.牛顿—莱布尼茨公式 5.换元积分公式与分部积分公式 6.广义积分 题型 题型I 利用定积分定义求极限 题型II比较定积分的大小 题型III利用积分估值定理解题 题型IV关于积分上限函数以及牛顿—莱布尼茨公式问题 题型V定积分的计算 题型VI 积分等式证明 题型VII 积分不等式证明 题型VIII 广义积分的计算 自测题五 1.根据极限计算定积分 2.根据定积分求导 3.求极限 4.求下列定积分 5.证明题 4月21日定积分练习题 基础题: 一.选择题、填空题 1.将和式的极限)0(.......321lim 1 >+++++∞→p n n P p p p p n 表示成定积分 ( ) A .dx x ?1 01 B .dx x p ?10 C .dx x p ?10)1( D .dx n x p ?10)( 2.将和式)21 .........2111(lim n n n n +++++∞→表示为定积分 . 3.下列等于1的积分是 ( ) A . dx x ? 1 B .dx x ?+1 )1( C .dx ? 1 1 D . dx ?1 021 4.dx x |4|1 02 ? -= ( ) A . 321 B .322 C .3 23 D . 3 25 5.曲线]2 3 ,0[,cos π∈=x x y 与坐标周围成的面积 ( ) A .4 B .2 C .2 5 D .3 6. dx e e x x ?-+1 )(= ( ) A .e e 1+ B .2e C .e 2 D .e e 1- 7.若10x m e dx =?,11e n dx x =?,则m 与n 的大小关系是( ) A .m n > B .m n < C .m n = D .无法确定 8. 按万有引力定律,两质点间的吸引力2 2 1r m m k F =,k 为常数,21,m m 为两质点的质量,r 为两点间距离,若两质点起始距离为a ,质点1m 沿直线移动至离2m 的距离为b 处,试求所作之功(b >a ) . 9.由曲线2 1y x =-和x 轴围成图形的面积等于S .给出下列结果: ① 1 21 (1)x dx --? ;②121 (1)x dx --?;③120 2(1)x dx -?;④0 21 2(1)x dx --?. 则S 等于( ) A .①③ B .③④ C .②③ D .②④ 10.0 (sin cos sin )x y t t t dt =+? ,则y 的最大值是( ) A .1 B .2 C .7 2 - D .0 11. 若()f x 是一次函数,且1 ()5f x dx =? ,1 017 ()6xf x dx =?,那么21()f x dx x ?的值是 . 12.???????=≠?=0 ,0,)()(2 x c x x dt t tf x F x ,其中)(x f 在0=x 处连续,且0)0(=f 若)(x F 在 0=x 处连续,则=c ( ) 。 (A).0=c ; (B).1=c ; (C).c 不存在; (D).1-=c . 高等数学三重积分计算方法总结 1、利用直角坐标计算三重积分: (1)投影法(先一后二): 1)外层(二重积分):区域Ω在xoy 面上的投影区域Dxy 2)内层(定积分): 从区域Ω的底面上的z 值,到区域Ω的顶面上的z 值。 (2)截面法(先二后一): 1)外层(定积分): 区域Ω在z 轴上的投影区间。 2)内层(二重积分):Ω垂直于z 轴的截面区域。 2、利用柱坐标计算三重积分 3、利用球面坐标计算三重积分 定限方法: (1)转面定θ(2)转线定φ (3)线段定r 4、利用对称性化简三重积分计算 设积分区域Ω关于xoy 平面对称, (1)若被积函数 f (x,y,z ) 是关于z 的奇函数,则三重积分为零。 (2)若被积函数 f (x,y,z ) 是关于z 的偶函数,则三重积分等于:在xoy 平面上方的半个Ω,区域上的三重积分的两倍. 使用对称性时应注意: 1)积分区域关于坐标面的对称性; 2)被积函数关于变量的奇偶性。 (cos ,sin ,)f z d d dz ρθρθρρθΩ???(,,)f x y z dv Ω=??? (,,)f x y z dxdydz Ω??? (sin cos ,sin sin ,cos )f r r r φθφθφΩ=???2 sin r drd d φφθ 例 计算 ,其中Ω是由曲面z = x 2 + y 2和x 2 + y 2 + z 2 =2所围成的空间闭区域. 解: 是关于x 的奇函数,且Ω关于 yoz 面对称 故其积分为零。 2x 2 y 是关于y 的奇函数,且关于 zox 面对称 ???Ω++dxdydz z y x x 2)(2 )(z y x x ++ 22222222)(zx xyz y x z y x x +++++=xyz z y x x 2)(222+++ ,022???Ω=∴ydv x ???Ω++=∴dxdydz z y x x I 2)(,22???Ω=zdxdydz x ???Ωθρρ??θρ=dz d d z 22cos 2????θρρθ=zdz d d 23cos 2 ??πρρ-ρ-θρθ=20104 223)2(cos d d 245π=222ρ-ρπ20 高考定积分应用常见题型大全 一.选择题(共21小题) 1.(2012?福建)如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为() A.B.C.D. 2.(2010?山东)由曲线y=x2,y=x3围成的封闭图形面积为() A.B.C.D. 3.设f(x)=,函数图象与x轴围成封闭区域的面积为() A.B.C.D. 4.定积分的值为() A.B.3+ln2 C.3﹣ln2 D.6+ln2 5.如图所示,曲线y=x2和曲线y=围成一个叶形图(阴影部分),其面积是() A.1B.C.D. 6.=() A.πB.2C.﹣πD.4 7.已知函数f(x)的定义域为[﹣2,4],且f(4)=f(﹣2)=1,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,则平面区域f(2a+b)<1(a≥0,b≥0)所围成的面积是() A.2B.4C.5D.8 8.∫01e x dx与∫01e x dx相比有关系式() A. ∫01e x dx<∫01e x dx B. ∫01e x dx>∫01e x dx C. (∫01e x dx)2=∫01e x dx D. ∫01e x dx=∫01e x dx 9.若a=,b=,则a与b的关系是() A.a<b B.a>b C.a=b D.a+b=0 10.的值是() A.B.C.D.11.若f(x)=(e为自然对数的底数),则=() A. +e2﹣e B. +e C. ﹣e2+e D. ﹣+e2﹣e 12.已知f(x)=2﹣|x|,则() A.3B.4C.3.5 D.4.5 13.设f(x)=3﹣|x﹣1|,则∫﹣22f(x)dx=() A.7B.8C.7.5 D.6.5 14.积分=() A.B.C.πa2D.2πa2 15.已知函数的图象与x轴所围成图形的面积为()A.1/2 B.1C.2D.3/2 归纳二重积分的计算方法 摘 要 :本文总结出了求二重积分的几种方法,比如用定义、公式、定理、性质求极限. 关键词 :函数极限;计算方法;洛必达法则; 四则运算 前言 二重积分的概念和计算是多元函数微积分学的重要部分,在几何\物理\力学等方面有着重要的应用.重积分是由一元函数积分推广而来的,但与一元函数相比,计算重积分的难度除了与被积函数有关外,还与积分区域的特点有关,计算重积分的主要思想方法是化重积分为累次积分.求二重积分的方法很多且非常灵活,本文归纳了二重积分计算的一些常见方法和技巧. 1. 预备知识 1.1二重积分的定义]1[ 设(),f x y 是定义在可求面积的有界区域D 上的函数. J 是一个确定的数,若对任给的正数 ε ,总存在某个正数δ,使对于D 的任意分割T ,当它的细度T δ<时,属于T 的所有积分和 都有 ()1 ,n i i i i f J ξησ ε=?-<∑, 则称(),f x y 在D 上可积,数J 称为函数(),f x y 在D 上的二重积分,记作 (),D J f x y d σ=??, 其中(),f x y 称为二重积分的被积函数, ,x y 称为积分变量, D 称为积分区域. 1.2二重积分的若干性质 1.21若(),f x y 在区域D 上可积, k 为常数,则(),kf x y 在D 上也可积,且 (),D kf x y d σ??(),D k f x y d σ=??. 1.22 若(),f x y ,(),g x y 在D 上都可积,则()(),,f x y g x y ±在D 上也可积,且 ()()[,,]D f x y g x y d σ±??()(),,D D f x y d g x y d σσ=±????. 1.23 若(),f x y 在1D 和2D 上都可积,且1D 与2D 无公共内点,则(),f x y 在12D D 上也可积,且 ()12 ,D D f x y d σ?? ()()1 2 ,,D D f x y d f x y d σσ=±???? 1.3在矩形区域上二重积分的计算定理 设(),f x y 在矩形区域D [][],,a b c d =?上可积,且对每个[],x a b ∈,积分(),d c f x y dy ?存 在,则累次积分(),b d a c dx f x y dy ??也存在,且 (),D f x y d σ?? (),b d a c dx f x y dy =??. 同理若对每个[],y c d ∈,积分(),b a f x y dx ?存在,在上述条件上可得 (),D f x y d σ?? (),d b c a dy f x y dx =?? 2.求的二重积分的几类理论依据 二重积分类似定积分,可看成一个函数在有界区域内的积分,它计算的主要思路是把重积分化为我们学过的累次积分的计算,在这思想下如何化为更容易求的累次积分成为问题关键,下文介绍了把区域化为简单的X -型\Y -型区域及把复杂的函数通过变量变换化为简单函数的几种计算技巧,另外还列举几类特殊二重积分的简单求法. 2.1在直角坐标系下,对一般区域二重积分的计算 X -型区域: ()()(){}12 ,,D x y y x y y x a x b =≤≤≤≤ Y -型区域: ()()(){}1 2 ,,D x y x y x x y c y d = ≤≤≤≤ 定理:若(),f x y 在X -区域D 上连续,其中()1y x ,()2y x 在[],a b 上连续,则 (),D f x y d σ??()()() 21,b y x a y x dx f x y dy =?? 即二重积分可化为先对y ,后对x 的累次积分. 同理在上述条件下,若区域为Y -型,有定积分计算例题
二重积分计算中的积分限的确定
定积分练习题
高等数学三重积分计算方法总结
(完整版)高考定积分练习题
归纳二重积分的计算方法