
3.17
(1)相关函数
仿真代码:
A1=getAk(SNR1);
A2=getAk(SNR2);
A3=getAk(SNR3); %求得信号的幅度;
noise=randn(1,N) + j*randn(1,N); % 构建高斯白噪声;
s1=getSk(A1,f1,N);
s2=getSk(A2,f2,N);
s3=getSk(A3,f3,N);; %产生3个复正弦信号
vn=s1+s2+s3+noise;
vk=fft(vn,2*N); %对v(n)补N个零,然后做2N点FFT
swk=((abs(vk)).^2)/N; %计算功率谱估计S(ω)
r0=ifft(swk); %对S(k)做ifft得到
r=[r0(N+2 : 2*N) , r0(1 : N)]; %根据教程3.1.8式可得
r1=xcorr(vn, N-1,'biased'); %直接计算自相关函数%%%%%%%%%%%%%%%%%%%%%%%%%取序列实部,虚部%%%%%% real_r=real(r);
imag_r=imag(r);
real_r1=real(r1);
imag_r1 = imag(r1);
subplot(2,2,1);
stem(real_r);
xlabel('基于FFT的自相关函数的实部');
ylabel('实部');
subplot(2,2,2);
stem(imag_r);
xlabel('基于FFT的自相关函数的虚部');
ylabel('虚部');
subplot(2,2,3);
stem(real_r1);
ylabel('实部');
xlabel('估计的自相关函数的实部');
subplot(2,2,4);
stem(imag_r1);
xlabel('估计的自相关函数的虚实部');
ylabel('虚部');
function AK=getAk(SNR) %求得幅度%%%%%%%%%%%%%%%%%%%由SNR=10log(A^2/2*σ^2) %%%%%%% AK=((10^(SNR/10))*2)^0.5;
function Sk=getSk(Ak,fk,N)
Sk=Ak * exp(j * 2 * pi * fk *(0:N-1));
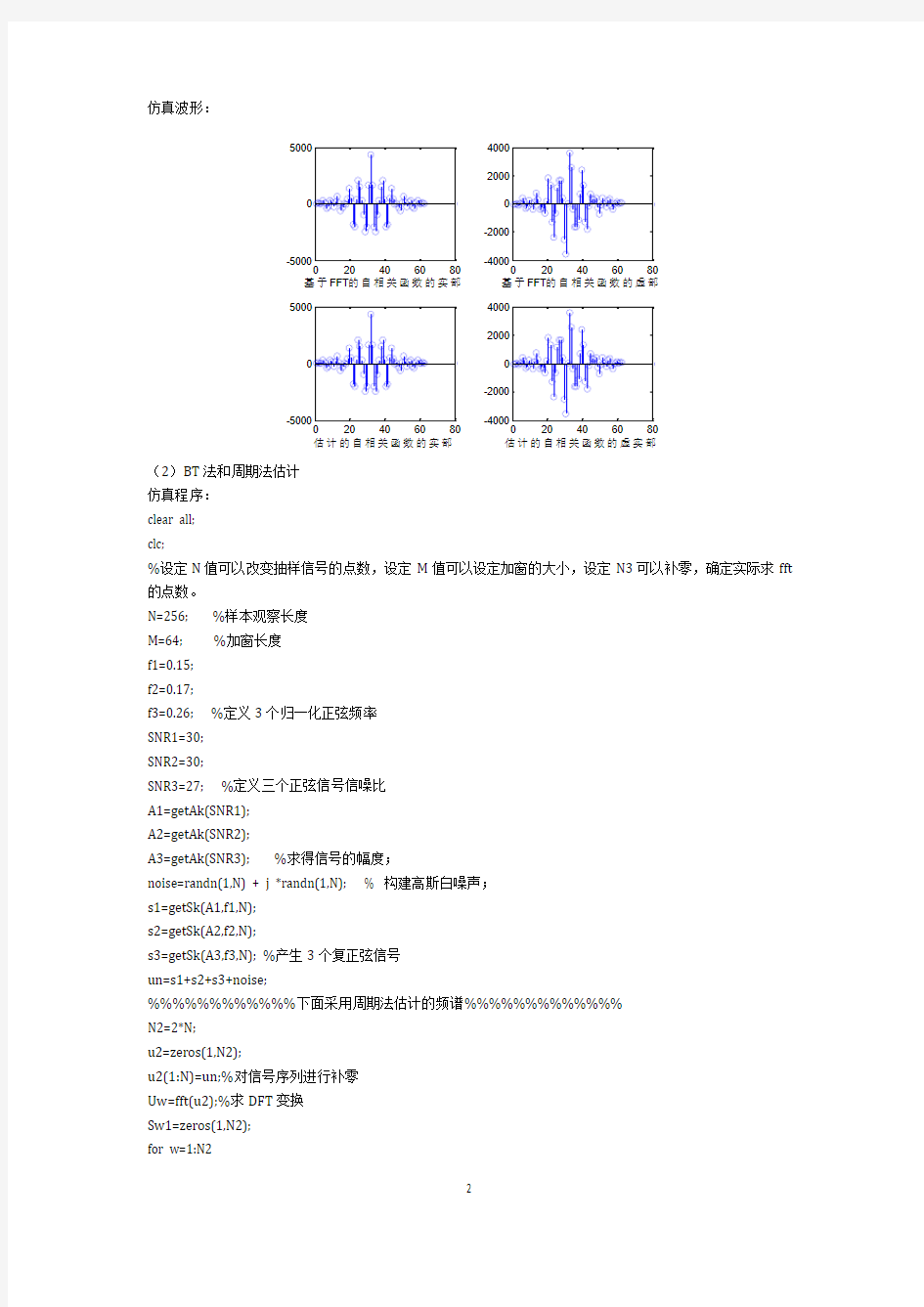
仿真波形:
(2)BT 法和周期法估计 仿真程序: clear all; clc;
%设定N 值可以改变抽样信号的点数,设定M 值可以设定加窗的大小,设定N3可以补零,确定实际求fft 的点数。
N=256; %样本观察长度 M=64; %加窗长度 f1=0.15; f2=0.17;
f3=0.26; %定义3个归一化正弦频率 SNR1=30; SNR2=30;
SNR3=27; %定义三个正弦信号信噪比 A1=getAk(SNR1); A2=getAk(SNR2);
A3=getAk(SNR3); %求得信号的幅度;
noise=randn(1,N) + j *randn(1,N); % 构建高斯白噪声; s1=getSk(A1,f1,N); s2=getSk(A2,f2,N);
s3=getSk(A3,f3,N); %产生3个复正弦信号 un=s1+s2+s3+noise;
%%%%%%%%%%%%下面采用周期法估计的频谱%%%%%%%%%%%%% N2=2*N; u2=zeros(1,N2);
u2(1:N)=un;%对信号序列进行补零 Uw=fft(u2);%求DFT 变换 Sw1=zeros(1,N2); for w=1:N2
基于FFT 的自相关函数的实部
实部
基于FFT 的自相关函数的虚部
虚
部
实部
估计的自相关函数的实部
估计的自相关函数的虚实部
虚部
Sw1(w)=((abs(Uw(w)))^2)/N;%计算功率谱
end
r0=zeros(1,N2);
r0=ifft(Sw1);
r=zeros(1,N2);
r(1:N)=r0(N+1:N2);
r(N+1:N2)=r0(1:N);
M=64;%加窗处理
for n=1:2*M
r1(n)=r((N2-2*M)/2+n);
end%加窗之后的序列为r1
N3=256;%实际进行fft变换的点数。
r2=zeros(1,N3);
r2(1:2*M)=r1;%将加窗之后的r1进行了补零得到的是r2.
Sw2=fft(r2);
Sw2=log10(abs(Sw2));%取模取对数
temp=zeros(1,N3/2);
temp=Sw2(1:N3/2);
Sw2(1:N3/2)=Sw2((N3/2+1):N3);
Sw2((N3/2+1):N3)=temp;%将0-2*pi的序列折换成-pi到pi的序列。d=1/(N3-1);
x=zeros(1,N3);
for i=1:N3
x(i)=-0.5+(i-1)*d;
end
Sw1=log10(abs(Sw1));%取模取对数
temp=zeros(1,N2/2);
temp=Sw1(1:N2/2);
Sw1(1:N2/2)=Sw1((N2/2+1):N2);
Sw1((N2/2+1):N2)=temp;%将0-2*pi的序列折换成-pi到pi的序列。l=1/(N2-1);
y=zeros(1,N2);
for k=1:N2
y(k)=-0.5+(k-1)*l;
end
subplot(1,2,1);
plot(x,Sw2);
xlabel('BT法');
ylabel('归一化的功率谱/dB');
subplot(1,2,2);
plot(y,Sw1);
xlabel('周期法');
ylabel('归一化的功率谱/dB');
仿真波形:
由仿真结果可以看出:BT 法和周期法在相同的阶数下,周期法比BT 法分辩率更高,但是波动比BT 法更大。
(3)Levinson-Durbin 迭代法 仿真代码: clear all; clc;
%设定N 值可以改变抽样信号的点数,设定M 值可以设定加窗的大小,设定N3可以补零,确定实际求fft 的点数。
N=256; %样本观察长度 p=16; %设定AR 模型参数 f1=0.15; f2=0.17;
f3=0.26; %定义3个归一化正弦频率 SNR1=30; SNR2=30;
SNR3=27; %定义三个正弦信号信噪比 A1=getAk(SNR1); A2=getAk(SNR2);
A3=getAk(SNR3); %求得信号的幅度;
noise=randn(1,N) + j *randn(1,N); % 构建高斯白噪声; s1=getSk(A1,f1,N); s2=getSk(A2,f2,N);
s3=getSk(A3,f3,N); %产生3个复正弦信号 un=s1+s2+s3+noise;
r0=xcorr(un, p,'biased'); %直接计算自相关函数 rp=r0(p+1:2*p+1);
%%%%%%%%Lervinson_Durbin 算法 %%%%%%%% a(1,1)=-rp(2)/rp(1);
e(1)=rp(1)-abs(rp(2))^2/rp(1); %计算σ1 b=0; for m=2:p
k(m)=-(rp(m+1)+sum(a(m-1,1:m-1).*rp(m:-1:2)))/e(m-1);
BT 法
归一化的功率谱/d B
周期法
归一化的功率谱/d B
a(m,m)=k(m);
for d=1:m-1
a(m,d)=a(m-1,d)+k(m)*conj(a(m-1,m-d));
end
e(m)=e(m-1)*(1-abs(k(m))^2);
end
%%%%计算16阶AR功率谱%%%%%%%%%%%%%%%%%%%%%% NF=1024; %%%FFT点数
Sw=e(p)./(abs(fft([1,a(p, :)],NF)).^2);
%%%%%%此下作用相当于函数fftshift
temp=zeros(1,NF/2);
temp=Sw(1:NF/2);
Sw(1:NF/2)=Sw((NF/2+1):NF);
Sw((NF/2+1):NF)=temp;%将0-2*pi的序列折换成-pi到pi的序列。
SAR=zeros(1,NF);
for w=1:NF
SAR(w)=log10((abs(Sw(w))^2));
end
d=1/(NF-1);
x=zeros(1,NF);
for i=1:NF
x(i)=-0.5+(i-1)*d;
end
plot(x,SAR);
xlabel('w/2π');
ylabel('归一化的功率谱/dB');
仿真波形:
3.20
(1)Root-MUSIC 仿真代码:clear all;
clc;
w/2π归
一
化
的
功
率
谱
/
d
B
N=1000; %样本个数
f1=0.5; %信号频率
f2=-0.3;
s1=getSk(f1,N); %产生第一个信号
s2=getSk(f2,N); %产生第二个信号
noise=(randn(1,N) + j*randn(1,N))/sqrt(2); % 构建高斯白噪声;
un=s1+s2+noise; %产生带噪声的信号
K=2; %信号源个数
M=8; %自相关矩阵阶数
R=getR(un,N,M); %根据教材3-5-18求自相关矩阵
%%%%%%%root_MUSIC进行频率估计%%%%%%%%%%%%%
[U,E]=svd(R); %矩阵U是特征值向量组成的矩阵,E是对角矩阵,对角矩阵的排列是从大到小
e=diag(E);
G=U(:,3:M);
GG=G*G';
co=zeros(2*M-1,1); %由教材可知是关于变量z的2(M-1)次方程,共有2(M-1)个根for m=1:M
co(m:m+M-1)=co(m:m+M-1)+GG(M:-1:1,m);
end
z=roots(co); %求多项式的跟
erro=abs(abs(z)-1);%除掉大于1的增根(方程式在此条件下变形的)
ph=angle(z)/(2*pi);
%挑选出最接近单位圆的N个根
disp(z)
disp(erro)
disp(ph)
function aw=getaw(w,M)
aw=zeros(M,1);
for j=1:M
aw(j)=exp(-w*(j-1)*i);
end
function R=getR(x,N,M)
L=N-M+1;
tempx=zeros(M,1);
R=zeros(M,M);
for n=M:N
for j=1:M
tempx(j)=x(n-(j-1));
end
R=R+tempx*tempx';
end
R=R/L;
function Sk=getSk(fk,N)
Sk=exp(j * 2 * pi * fk *(0:N-1)+j*2*pi*rand); %产生0到2π上均分布的随机相位信号
仿真结果:
w1= -0.3004 w2= 0.4996
(2)MUSIC算法
仿真程序:
clear all;
clc;
N=1000; %样本个数
f1=0.5; %信号频率
f2=-0.3;
s1=getSk(f1,N); %产生第一个信号
s2=getSk(f2,N); %产生第二个信号
noise=(randn(1,N) + j*randn(1,N))/sqrt(2); % 构建高斯白噪声;
un=s1+s2+noise; %产生带噪声的信号
K=2; %信号源个数
M=8; %自相关矩阵阶数
R=getR(un,N,M); %根据教材3-5-18求自相关矩阵
NF=2048; %定义扫描点数
%%%%%%%MUSIC进行谱峰收索%%%%%%%%%%%%%
[U,E]=svd(R); %矩阵U是特征值向量组成的矩阵,E是对角矩阵,对角矩阵的排列是从大到小
e=diag(E);
G=U(:,3:M);
d=1/(NF-1);%求画图用的横坐标的间隔。
h=zeros(1,NF);
for i=1:NF
h(i)=-0.5+(i-1)*d;
end
y=zeros(1,NF);
for j=1:NF
w=h(j)*2*pi;
aw=getaw(w,M);
y(j)=log10(abs(1/((aw')*G*(G')*aw)));
end
plot(h,y);
xlabel('w/2π');
ylabel('归一化的功率谱/dB');
title('MUSIC谱估计')
仿真波形:
由仿真结果可知:Root-MUSIC 算法与MUSIC 算法相比,两者误差都很小。
3.21 ESPRIT 算法 仿真代码: clear all; clc;
format long
N=1000; %样本个数 f1=0.5; %信号频率 f2=-0.3;
s1=getSk(f1,N); %产生第一个信号 s2=getSk(f2,N); %产生第二个信号
noise=(randn(1,N) + j*randn(1,N))/sqrt(2); % 构建高斯白噪声; un=s1+s2+noise; %产生带噪声的信号 K=2; %信号源个数
M=8; %自相关矩阵阶数 [X,R]=corrmtx(un,M); Rxx=R(1:M,1:M);
Rxy=R(1:M,2:M+1); %计算Rxy
%%%%%%%EPRIT 进行频率估计%%%%%%%%%%%%% [U,E]=svd(Rxx); e=diag(E);
emin=e(end); %获取最小特征值
%%%构造Z 矩阵%%%%%%%%%%%%%%%%%%%%%%%%%%%% Z=zeros(M,M); for i=1:M-1 Z(i,i+1)=1; end
Cxx=Rxx-emin*eye(M); Cxy=Rxy-emin*Z; [U,E]=eig(Cxx,Cxy);
w/2π
归一化的功率谱/d B
MUSIC 谱估计
z=diag(E);
ph=angle(z)/(2*pi); %求所有特征值的相应归一化特征值
erro=abs(abs(z)-1); %与单位圆之间的距离
disp(ph);
disp(erro);
function R=getR(x,N,M)
L=N-M+1;
tempx=zeros(M,1);
R=zeros(M,M);
for n=M:N
for j=1:M
tempx(j)=x(n-(j-1));
end
R=R+tempx*tempx';
end
R=R/L;
function Sk=getSk(fk,N)
Sk=exp(j * 2 * pi * fk *(0:N-1)+j*2*pi*rand); %产生0到2π上均分布的随机相位信号
仿真结果:
w1= 0.496818689408838 w2= -0.285563358651823
4.18
仿真代码:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %
%程序功能:产生512点的样本函数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %
clear all;
clc;
N=512; %样本序列长度
M=100; %独立试验次数
sigma_v_2=0.0731;
vn=sqrt(sigma_v_2)*randn(N,1,M); %产生均值为零,方差为0.0731的加性噪声,产生100次512X1的噪声用于100次独立试验
u0=[0 0];
a=[1 -0.975 0.95];
un=filter(1,a,vn); %构建AR模型,其中vn为输入,un为输出,产生100组独立信号1x512
%display(un);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %程序功能:用LMS算法来估计w1,w2
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% u1=0.05; %定义两个步长
u2=0.005;
w1=zeros(2,N,M); %初始化权向量.两个列向量对应要估计的w1,w2 100个2xN权向量
w2=zeros(2,N,M); %分别针对u1=0.05,u2=0.005
for m=1:M; %100次独立实验
e1(:,:,m)=zeros(N,1); %初始化相关参数
e2(:,:,m)=zeros(N,1);
d1(:,:,m)=zeros(N,1);
d2(:,:,m)=zeros(N,1);
for n=3:N-1 %信号向量时刻迭代
w1(:,n+1,m)=w1(:,n,m)+u1*un(n-1:-1:n-2,:,m)*conj(e1(n,1,m));
w2(:,n+1,m)=w2(:,n,m)+u2*un(n-1:-1:n-2,:,m)*conj(e2(n,1,m));
d1(n+1,1,m)=w1(:,n+1,m)'*un(n:-1:n-1,:,m);
d2(n+1,1,m)=w2(:,n+1,m)'*un(n:-1:n-1,:,m);
e1(n+1,1,m)=un(n+1,:,m)-d1(n+1,1,m);
e2(n+1,1,m)=un(n+1,:,m)-d2(n+1,1,m);
end
end
w1_ave=zeros(2,N);
w2_ave=zeros(2,N);
e1_ave=zeros(N,1);
e2_ave=zeros(N,1);
for m=1:M
w1_ave=w1_ave+w1(:,:,m);
w2_ave=w2_ave+w2(:,:,m);
e1_ave=e1_ave+e1(:,:,m).^2;
e2_ave=e2_ave+e2(:,:,m).^2;
end
w1_ave=w1_ave/M; %100次独立实验权向量的均值
w2_ave=w2_ave/M;
e1_ave=e1_ave/M; %100次独立实验的学习曲线均值
e2_ave=e2_ave/M;
t=1:N;
figure(1)
plot(t,w1(1,:,100),t,w1(2,:,100),t,w1_ave(1,:),t,w1_ave(2,:))
xlabel('迭代次数');ylabel('权向量')
title('步长=0.05')
figure(2)
plot(t,w2(1,:,100),t,w2(2,:,100),t,w2_ave(1,:),t,w2_ave(2,:))
xlabel('迭代次数');ylabel('权向量')
title('步长=0.005')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%程序功能:独立实验100次计算剩余误差和失调参数,画出学习曲线%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% wopt=zeros(2,M);
Jmin=zeros(1,M);
sum_eig=zeros(M,1);
%%%%通过维纳-霍夫方程计算最小均方误差
%直接计算自相关函数
for m=1:M
rm=xcorr(un(:,:,m),'biased');
R =[rm(512),rm(513);rm(511),rm(512)];
p =[rm(512);rm(510)];
wopt(:,m)=R\p; %单次最佳权值
[v,d]=eig(R);
Jmin(m)=rm(512)-p'*wopt(:,m); %单次最小均方误差
sum_eig(m)=d(1,1)-d(2,2); %单次特征值求和
end
sJmin=sum(Jmin)/M; %100次平均误差
Jex1=e1_ave-sJmin;
Jex2=e2_ave-sJmin; %计算剩余均方误差
sum_eig_100=sum(sum_eig)/M; %100次特征值总和
Jexfin1=u1*sJmin*(sum_eig_100/(2-u1*sum_eig_100));
Jexfin2=u2*sJmin*(sum_eig_100/(2-u2*sum_eig_100));
M1=Jexfin1/sJmin; %失调参数m1
M2=Jexfin2/sJmin; %失调参数m2
figure(3)
plot(t,e1_ave,'*',t,e2_ave,'r');
xlabel('迭代次数');
ylabel('均方误差');
legend('u1=0.05','u2=0.005')
title('学习曲线');
axis([0,600,0,1])
display(M1);
display(M2);
仿真波形:
M1 = -0.002061056056484 M2 = -2.064886318291408e-04
由仿真结果可知:当步长较大时,收敛速度较快,但失调和剩余均方误差较大,从而使稳态性能变差;而步长较小时,收敛速度虽然较慢,但失调和剩余均方误差减小,从而可以改善稳态性能;
问题:当计算失调参数时,采用教材式(4.4.28)时,仿真得到的失调参数,较式(4.4.27)误差较大。分析原因,式(4.4.28)只有在步长非常小时,误差才小。
%M1=u1*sum_eig_100/(2-u1*sum_eig_100); %由教材式(4.4.28) %M2=u2*sum_eig_100/(2-u2*sum_eig_100);
迭代次数
权向量
步长=0.05
迭代次数
权向量
步长=0.005
迭代次数
均方误差
学习曲线
5.10 仿真结果及图形
(1) M=2时,210.99,0.93627a σ=-= ,求解Yule-Walker 方程
211(0)(1)(1)(0)0r r a r r σ??????=????????????
得到相关矩阵
247.048746.578346.578347.0487R ??=????
计算程序为:
%由yuler-walker 方程计算M=2时的自相关矩阵 r2=inv([1,-0.99;-0.99,1]) * [v_sigmal;0]; R2=[r2(1),r2(2);r2(2),r2(1)]; %M1=2
(2) M=3时,
2
120.99,0,0.93627a a σ=-== ,求解Yule-Walker 方程 2
12(0)(1)(2)1(1)(0)(1)0(2)(1)(0)0r r r r r r a r r r a σ????????????=??
????????????????
得到自相关矩阵为
347.048746.578346.112546.578347.048746.578346.112546.578347.0487R ????=??
????
计算程序为:
r3=inv([1,-0.99,0;-0.99,1,0;0,-0.99,1])*[0.93627;0;0];
R3=[r3(1),r3(2),r3(3);r3(2),r3(1),r3(2);r3(3),r3(2),r3(1)]; % M2=3 (3) 计算特征值扩展
%%%%%%%计算特征扩展值%%%%%%%% eig1=eig(R2); %计算特征值 eig2=eig(R3);
eig_spread1=max(eig1)/min(eig1);
eig_spread2=max(eig2)/min(eig2);
%display(eig_spread1);
%display(eig_spread2);
M=2时特征值扩展是199.0000;
M=3时特征值扩展是444.2790。
(4) 根据LMS算法均方误差收敛特性,M=2时步长因子应在区间(0,0.0106)之间,M=3时,步长因子应在区间(0,0.00708)之间,因此题中的步长因子不合理,仿真时不收敛。故在仿真中,M=2时采用步长因子0.001,M=3时采用步长因子0.0006.
仿真程序:%%%%%%%%%用LMS算法实现对u(n)的线性预测估计%%%%%%%%%%%% clear all;
clc;
M1=2;
M2=3; %滤波器权系数参数
L=10000; %产生系统输入白噪声点数,用于迭代次数
v_sigmal=0.93627; %v(n)的方差
N=100; %独立试验次数500次
v=sqrt(v_sigmal)*randn(L,1,N); %产生均值为零,方差为0.93627的加性噪声,产生500次5000x1的噪声用于500次独立试验
a=[1 -0.99];
u=filter(1,a,v); %构建AR模型,其中v为输入,u为输出,产生500组独立信号5000x1
%由yuler-walker方程计算M=2时的自相关矩阵
r2=inv([1,-0.99;-0.99,1]) * [v_sigmal;0];
R2=[r2(1),r2(2);r2(2),r2(1)]; %M1=2
% display(R2);
r3=inv([1,-0.99,0;-0.99,1,0;0,-0.99,1])*[0.93627;0;0];
R3=[r3(1),r3(2),r3(3);r3(2),r3(1),r3(2);r3(3),r3(2),r3(1)]; % M2=3
% display(R3);
%%%%%%%计算特征扩展值%%%%%%%%
eig1=eig(R2); %计算特征值
eig2=eig(R3);
eig_spread1=max(eig1)/min(eig1);
eig_spread2=max(eig2)/min(eig2);
%display(eig_spread1);
%display(eig_spread2);
%用LMS算法实现对u(n)的线性预测估计
mu1=0.001;
mu2=0.0005;
w1=zeros(M1,L,N); %初始化权向量.两个列向量对应要估计的w1,w2 500个2xN权向量w2=zeros(M2,L,N); %分别针对M1,M2
for m=1:N %独立试验500次针对mu1,w1两个权系数
e1(:,:,m)=zeros(L,1); %初始化相关参数
d1(:,:,m)=zeros(L,1);
for n=3:L-1
w1(:,n+1,m)=w1(:,n,m)+mu1*u(n-1:-1:n-2,:,m)*conj(e1(n,1,m));
d1(n+1,1,m)=w1(:,n+1,m)'*u(n:-1:n-1,:,m);
e1(n+1,1,m)=u(n+1,:,m)-d1(n+1,1,m);
end
end
for m=1:N %独立试验500次针对mu2,w2三个权系数
%初始化相关参数
e2(:,:,m)=zeros(L,1);
d2(:,:,m)=zeros(L,1);
for n=4:L-1
w2(:,n+1,m)=w2(:,n,m)+mu2*u(n-1:-1:n-3,:,m)*conj(e2(n,1,m));
d2(n+1,1,m)=w2(:,n+1,m)'*u(n:-1:n-2,:,m);
e2(n+1,1,m)=u(n+1,:,m)-d2(n+1,1,m);
end
end
w1_ave=zeros(M1,L);
w2_ave=zeros(M2,L);
e1_ave=zeros(L,1);
e2_ave=zeros(L,1);
for m=1:N
w1_ave=w1_ave+w1(:,:,m);
w2_ave=w2_ave+w2(:,:,m);
e1_ave=e1_ave+e1(:,:,m).^2;
e2_ave=e2_ave+e2(:,:,m).^2;
end
w1_ave=w1_ave/N; %500次独立实验权向量的均值
w2_ave=w2_ave/N;
e1_ave=e1_ave/N; %5100次独立实验的学习曲线均值
e2_ave=e2_ave/N;
t=1:L;
figure(1)
plot(t,w1(1,:,100),t,w1(2,:,100),t,w1_ave(1,:),t,w1_ave(2,:));
xlabel('迭代次数n'); ylabel('抽头权值');
title('M1=2,步长0.001的权向量收敛曲线')
figure(2)
plot(t,e1_ave);
xlabel('迭代次数n'); ylabel('MSE');title('M1=2,步长0.001的学习曲线');
figure(3)
plot(t,w2(1,:,100),t,w2(2,:,100),t,w2(3,:,100),t,w2_ave(1,:),t,w2_ave(2,:),t,w2_ave(3,:)); xlabel('迭代次数n'); ylabel('抽头权值');
title('M2=3,步长0.0005的权向量收敛曲线')
figure(4)
plot(t,e2_ave);
xlabel('迭代次数n'); ylabel('MSE');title('M1=2,步长0.0005的学习曲线'); 仿真波形图:
迭代次数n
抽头权值
M1=2,步长0.001的权向量收敛曲
线
迭代次数n
抽头权
值
M2=3,步长0.0005的权向量收敛曲线
迭代次数n
M S E
M1=2,步长0.001的学习曲线
另附课本中5.2.4 burg 算法功率谱估计仿真代码及波形
仿真程序:%%%%%%%%%%利用Burg 算法进行功率谱估计%%%%%%%%%%%%%%%% clear all; clc;
N=256; %观测样本数
M=16; %BURG 算法的阶数 sigmal_v=0.001; %定义噪声方差 f1=0.1; f2=0.25;
f3=0.27; %定义3个归一化正弦频率 A1=1; A2=1;
A3=0.5; %定义三个正弦信号幅度
v=sigmal_v*randn(1,N) + j*sigmal_v*randn(1,N); % 构建高斯白噪声; s1=getSk(A1,f1,N); s2=getSk(A2,f2,N);
s3=getSk(A3,f3,N); %产生3个复正弦信号 u=s1+s2+s3+v; %构造观测信号 k=zeros(1,M); a=zeros(M,M); ef=zeros(N,M); eb=zeros(N,M); ef(1:N,1)=u;
eb(1:N,1)=u; %burg 算法的初始化,ef,eb 表示格形滤波器的各阶状态,算法中的重要参数 a(1,1)=(-2)*(eb(1:N-1,1)'*ef(2:N,1))/(ef(2:N,1)'*ef(2:N,1)+eb(1:N-1,1)'*eb(1:N-1,1)); k(1,1)=a(1,1);
ef(2:N,2)=ef(2:N,1)+k(1,1)*eb(1:N-1,1);
eb(2:N,2)=eb(1:N-1,1)+conj(k(1,1))*ef(2:N,1); %BURG 算法 步骤2 %%%burg 算法 步骤3
for i=2:M %计算M 阶滤波器参数,实现burg 算法,用递归实现
a(i,i)=(-2)*(eb(i:N-1,i)'*ef(i+1:N,i))/(ef(i+1:N,i)'*ef(i+1:N,i)+eb(i:N-1,i)'*eb(i:N-1,i));
迭代次数n
M S E
M2=3,步长0.0006的学习曲线
k(1,i)=a(i,i);
ef(i+1:N,i+1)=ef(i+1:N,i) +k(1,i)*eb(i:N-1,i);
eb(i+1:N,i+1)=eb(i:N-1,i)+conj(k(1,i))*ef(i+1:N,i); for j=1:i-1
a(i,j)=a(i-1,j)+k(1,i)*conj(a(i-1,i-j)); end end
NF=1024; %%%FFT 点数
Sw=sigmal_v./fftshift((abs(fft([1,a(M,:)],NF)).^2)); for w=1:NF
SAR(w)=log10((abs(Sw(w))^2)); end
d=1/(NF-1); x=zeros(1,NF); for i=1:NF
x(i)=-0.5+(i-1)*d; end plot(x,SAR); xlabel('w/2π');
ylabel('归一化的功率谱/dB');
function Sk=getSk(Ak,fk,N)
Sk=Ak * exp(j * 2 * pi * fk *(0:N-1));
仿真波形:
w/2π
归一化的功率谱/d B
6.13仿真结果及图形
仿真代码:
%%%%%%%%%%%%%%基于奇异值分解的MVDR方法进行信号频率估计%%%%%%%%%%%% clear all;
clc;
N=1000; %样本点数
M=32; %FIR阶数
% M=4;
f1=0.1;
f2=0.25;
f3=0.27; %定义3个归一化正弦频率
SNR1=30;
SNR2=30;
SNR3=27; %定义三个正弦信号信噪比
A1=getAk(SNR1);
A2=getAk(SNR2);
A3=getAk(SNR3); %求得信号的幅度;
s1=getSk(A1,f1,N);
s2=getSk(A2,f2,N);
s3=getSk(A3,f3,N); %产生3个复正弦信号
noise=randn(1,N) + j*randn(1,N); % 构建高斯白噪声1x1000;
u=s1+s2+s3+noise; %输入信号
%% 构建矩阵
A=zeros(M,N-M+1);
for n=1:N-M+1
A(:,n)=u(M+n-1:-1:n);
end
[U,S,V]=svd(A');
invphi=V*inv(S'*S)*V';
%% 构建向量
P=1024;
f=linspace(-0.5,0.5,P);
w=2*pi*f;
aw=zeros(M,P);
for k=1:P
for m=1:M
aw(m,k)=exp(-1i*w(k)*(m-1));
end
end
%% 计算MVDR谱
Pmvdr=zeros(size(w));
for k=1:P
Pmvdr(k)=1/(aw(:,k)'*invphi*aw(:,k));
end
实验6 数字滤波器的网络结构 一、实验目的: 1、加深对数字滤波器分类与结构的了解。 2、明确数字滤波器的基本结构及其相互间的转换方法。 3、掌握用MA TLAB 语言进行数字滤波器结构间相互转换的子函数及程序编写方法。 二、实验原理: 1、数字滤波器的分类 离散LSI 系统对信号的响应过程实际上就是对信号进行滤波的过程。因此,离散LSI 系统又称为数字滤波器。 数字滤波器从滤波功能上可以分为低通、高通、带通、带阻以及全通滤波器;根据单位脉冲响应的特性,又可以分为有限长单位脉冲响应滤波器(FIR )和无限长单位脉冲响应滤波器(IIR )。 一个离散LSI 系统可以用系统函数来表示: M -m -1-2-m m m=0 012m N -1-2-k -k 12k k k=1 b z b +b z +b z ++b z Y(z)b(z)H(z)=== =X(z)a(z) 1+a z +a z ++a z 1+a z ∑∑ 也可以用差分方程来表示: N M k m k=1 m=0 y(n)+a y(n-k)=b x(n-m)∑∑ 以上两个公式中,当a k 至少有一个不为0时,则在有限Z 平面上存在极点,表达的是以一个IIR 数字滤波器;当a k 全都为0时,系统不存在极点,表达的是一个FIR 数字滤波器。FIR 数字滤波器可以看成是IIR 数字滤波器的a k 全都为0时的一个特例。 IIR 数字滤波器的基本结构分为直接Ⅰ型、直接Ⅱ型、直接Ⅲ型、级联型和并联型。 FIR 数字滤波器的基本结构分为横截型(又称直接型或卷积型)、级联型、线性相位型及频率采样型等。本实验对线性相位型及频率采样型不做讨论,见实验10、12。 另外,滤波器的一种新型结构——格型结构也逐步投入应用,有全零点FIR 系统格型结构、全极点IIR 系统格型结构以及全零极点IIR 系统格型结构。 2、IIR 数字滤波器的基本结构与实现 (1)直接型与级联型、并联型的转换 例6-1 已知一个系统的传递函数为 -1-2-3 -1-2-3 8-4z +11z -2z H(z)=1-1.25z +0.75z -0.125z 将其从直接型(其信号流图如图6-1所示)转换为级联型和并联型。
例6.11 利用卡尔曼滤波估计一个未知常数 题目: 设已知一个未知常数x 的噪声观测集合,已知噪声v(n)的均值为零, 方差为 ,v(n)与x 不相关,试用卡尔曼滤波估计该常数 题目分析: 回忆Kalman 递推估计公式 由于已知x 为一常数,即不随时间n 变化,因此可以得到: 状态方程: x(n)=x(n-1) 观测方程: y(n)=x(n)+v(n) 得到A(n)=1,C(n)=1, , 将A(n)=1,代入迭代公式 得到:P(n|n-1)=P(n-1|n-1) 用P(n-1)来表示P(n|n-1)和P(n-1|n-1),这是卡尔曼增益表达式变为 从而 2v σ1??(|1)(1)(1|1)(|1)(1)(1|1)(1)()()(|1)()[()(|1)()()]???(|)(|1)()[()()(|1)](|)[()()](|1)H w H H v x n n A n x n n P n n A n P n n A n Q n K n P n n C n C n P n n C n Q n x n n x n n K n y n C n x n n P n n I K n C n P n n --=----=----+=--+=-+--=--2()v v Q n σ=()0w Q n =(|1)(1)(1|1)(1)()H w P n n A n P n n A n Q n -=----+21 ()(|1)[(|1)]v K n P n n P n n σ-=--+22(1)()[1()](1)(1)v v P n P n K n P n P n σσ-=--=-+
现代数字信号处理仿真作业 1.仿真题3.17 仿真结果及图形: 图 1 基于FFT的自相关函数计算
图 3 周期图法和BT 法估计信号的功率谱 图 2 基于式3.1.2的自相关函数的计算
图 4 利用LD迭代对16阶AR模型的功率谱估计16阶AR模型的系数为: a1=-0.402637623107952-0.919787323662670i; a2=-0.013530139693503+0.024214641171318i; a3=-0.074241889634714-0.088834852915013i; a4=0.027881022353997-0.040734794506749i; a5=0.042128517350786+0.068932699075038i; a6=-0.0042799971761507 + 0.028686095385146i; a7=-0.048427890183189 - 0.019713457742372i; a8=0.0028768633718672 - 0.047990801912420i a9=0.023971346213842+ 0.046436389191530i; a10=0.026025963987732 + 0.046882756497113i; a11= -0.033929397784767 - 0.0053437929619510i; a12=0.0082735406293574 - 0.016133618316269i; a13=0.031893903622978 - 0.013709547028453i ; a14=0.0099274520678052 + 0.022233240051564i; a15=-0.0064643069578642 + 0.014130696335881i; a16=-0.061704614407581- 0.077423818476583i. 仿真程序(3_17): clear all clc %% 产生噪声序列 N=32; %基于FFT的样本长度
LMS 算法MATLAB 实现结果及其分析 一、LMS :为课本155页例题 图1.1:LMS 算法学习曲线(初始权向量[]T 00w ?=) 图1.2滤波器权系数迭代更新过程曲线(步长075.0=μ) 图1.3滤波器权系数迭代更新过程曲线(步长025.0=μ)图1.4滤波器权系数迭代更新过程曲线(步长015.0=μ) 分析解释: 在图1.1中,收敛速度最慢的是步长为015.0=μ的曲线,收敛速度最快的是步长075.0=μ的曲线,所以可以看出LMS 算法的收敛速度随着步长参数的减小而相应变慢。图1.2、1.3、1.4分别给出了步长为075.0=μ、025.0=μ、025.0=μ的滤波器权系数迭代更新过程曲线,可以发现其不是平滑的过程,跟最抖下降法不一样,体现了其权向量是一个随机过程向量。
LMS2:为课本155页例题,156页图显示结果 图2.1:LMS 算法学习曲线(初始权向量[]T 00w ?=) 图2.2滤波器权系数迭代更新过程曲线(步长025.0=μ) 图2.3滤波器权系数迭代更新过程曲线(步长025.0=μ)图2.4最陡下降法权值变化曲线(步长025.0=μ) 分析解释: 图2.1给出了步长为025.0=μ的学习曲线,图2.2给出了滤波器权向量的单次迭代结果。图2.3给出了一 次典型实验中所得到的权向量估计()n w ?=,以及500次独立实验得到的平均权向量()}n w ?E{=的估计,即()∑==T t n w T 1 t )(?1n w ?,其中)(?n w t 是第t 次独立实验中第n 次迭代得到的权向量,T 是独立实验次数。可以发现,多次独立实验得到的平均权向量()}n w ?E{=的估计平滑了随机梯度引入的梯度噪声,使得其结果与使用最陡下降法(图2.4)得到的权向量趋于一致,十分接近理论最优权向量[]T 7853.08361.0w 0-=。 LMS3:为课本172页习题答案
数字信号处理作业
DFT 习题 1. 如果)(~n x 是一个周期为N 的周期序列,那么它也是周期为N 2的周期序列。把)(~ n x 看作周期为N 的周期序列,令)(~1k X 表示)(~n x 的离散傅里叶级数之系数,再把)(~ n x 看作周期为N 2的周期序列,再令)(~2k X 表示)(~n x 的离散傅里叶级数之系数。当然,)(~1k X 是周期性的,周期为N ,而)(~2k X 也是周期性的,周期为N 2。试利用)(~1k X 确定)(~2k X 。(76-4)
2. 研究两个周期序列)(~n x 和)(~n y 。)(~n x 具有周期N ,而)(~ n y 具有周期M 。序列)(~n w 定义为)()()(~ ~~n y n x n w +=。 a. 证明)(~n w 是周期性的,周期为MN 。 b. 由于)(~n x 的周期为N ,其离散傅里叶级数之系数)(~k X 的周期也是N 。类似地, 由于)(~n y 的周期为M ,其离散傅里叶级数之系数)(~k Y 的周期也是M 。)(~n w 的离散傅里叶级数之系数)(~k W 的周期为MN 。试利用)(~k X 和)(~k Y 求)(~k W 。(76-5)
3. 计算下列各有限长度序列DFT (假设长度为N ): a. )()(n n x δ= b .N n n n n x <<-=000) ()(δ c .10)(-≤≤=N n a n x n (78-7) 4. 欲作频谱分析的模拟数据以10千赫速率被取样,且计算了1024个取样的离散傅里叶变换。试求频谱取样之间的频率间隔,并证明你的回答。(79 -10)
卫星轨迹 一.问题提出 设卫星在空中运行的运动方程为: 其中是k 重力系数(k=401408km3/s)。卫星轨道采用极坐标表示,通过仿真,研究发射速度对卫星轨道的影响。实验将作出卫星在地球表面(r=6400KM ,θ=0)分别以v=8KM/s,v=10KM/s,v=12KM/s 发射时,卫星绕地球运行的轨迹。 二.问题分析 1.卫星运动方程一个二阶微分方程组,应用Matlab 的常微分方程求解命令ode45求解时,首先需要将二阶微分方程组转换成一阶微分方程组。若设,则有: 2.建立极坐标如上图所示,初值分别为:卫星径向初始位置,即地球半径:y(1,1)=6400;卫星初始角度位置:y(2,1)=0;卫星初始径向线速度:y(3,1)=0;卫星初始周向角速度:y(4,1)=v/6400。 3.将上述一阶微分方程及其初值带入常微分方程求解命令ode45求解,可得到一定时间间隔的卫星的径向坐标值y(1)向量;周向角度坐标值y(2)向量;径向线速度y(3)向量;周向角速度y(4)向量。 4.通过以上步骤所求得的是极坐标下的解,若需要在直角坐标系下绘制卫星的运动轨迹,还需要进行坐标变换,将径向坐标值y(1)向量;周向角度坐标值y(2)向量通过以下方程转换为直角坐标下的横纵坐标值X,Y 。 5.卫星发射速度速度的不同将导致卫星的运动轨迹不同,实验将绘制卫星分别以v=8KM/s ,v=10KM/s ,v=12KM/s 的初速度发射的运动轨迹。 三.Matlab 程序及注释 1.主程序 v=input('请输入卫星发射速度单位Km/s :\nv=');%卫星发射速度输入。 axis([-264007000-1000042400]);%定制图形输出坐标范围。 %为了直观表达卫星轨迹,以下语句将绘制三维地球。 [x1,y1,z1]=sphere(15);%绘制单位球。 x1=x1*6400;y1=y1*6400;???????-=+-=dt d dt dr r dt d dt d r r k dt r d θ θθ2)(2 22222θ==)2(,)1(y r y ?????????????**-=**+*-===)1(/)4()3(2)4()4()4()1()1()1()3()4()2() 3()1(y y y dt dy y y y y y k dt dy y dt dy y dt dy ???*=*=)] 2(sin[)1(Y )]2(cos[)1(X y y y y
实验5 抽样定理 一、实验目的: 1、了解用MA TLAB 语言进行时域、频域抽样及信号重建的方法。 2、进一步加深对时域、频域抽样定理的基本原理的理解。 3、观察信号抽样与恢复的图形,掌握采样频率的确定方法和插公式的编程方法。 二、实验原理: 1、时域抽样与信号的重建 (1)对连续信号进行采样 例5-1 已知一个连续时间信号sin sin(),1Hz 3 ππ=0001f(t)=(2f t)+6f t f ,取最高有限带宽频率f m =5f 0,分别显示原连续时间信号波形和F s >2f m 、F s =2f m 、F s <2f m 三情况下抽样信号的波形。 程序清单如下: %分别取Fs=fm ,Fs=2fm ,Fs=3fm 来研究问题 dt=0.1; f0=1; T0=1/f0; m=5*f0; Tm=1/fm; t=-2:dt:2; f=sin(2*pi*f0*t)+1/3*sin(6*pi*f0*t); subplot(4,1,1); plot(t,f); axis([min(t),max(t),1.1*min(f),1.1*max(f)]); title('原连续信号和抽样信号'); for i=1:3; fs=i*fm;Ts=1/fs; n=-2:Ts:2; f=sin(2*pi*f0*n)+1/3*sin(6*pi*f0*n); subplot(4,1,i+1);stem(n,f,'filled'); axis([min(n),max(n),1.1*min(f),1.1*max(f)]); end 程序运行结果如图5-1所示:
原连续信号和抽样信号 图5-1 (2)连续信号和抽样信号的频谱 由理论分析可知,信号的频谱图可以很直观地反映出抽样信号能否恢复原模拟信号。因此,我们对上述三种情况下的时域信号求幅度谱,来进一步分析和验证时域抽样定理。 例5-2编程求解例5-1中连续信号及其三种抽样频率(F s>2f m、F s=2f m、F s<2f m)下的抽样信号的幅度谱。 程序清单如下: dt=0.1;f0=1;T0=1/f0;fm=5*f0;Tm=1/fm; t=-2:dt:2;N=length(t); f=sin(2*pi*f0*t)+1/3*sin(6*pi*f0*t); wm=2*pi*fm;k=0:N-1;w1=k*wm/N; F1=f*exp(-j*t'*w1)*dt;subplot(4,1,1);plot(w1/(2*pi),abs(F1)); axis([0,max(4*fm),1.1*min(abs(F1)),1.1*max(abs(F1))]); for i=1:3; if i<=2 c=0;else c=1;end fs=(i+c)*fm;Ts=1/fs; n=-2:Ts:2;N=length(n); f=sin(2*pi*f0*n)+1/3*sin(6*pi*f0*n); wm=2*pi*fs;k=0:N-1; w=k*wm/N;F=f*exp(-j*n'*w)*Ts; subplot(4,1,i+1);plot(w/(2*pi),abs(F)); axis([0,max(4*fm),1.1*min(abs(F)),1.1*max(abs(F))]); end 程序运行结果如图5-2所示。 由图可见,当满足F s≥2f m条件时,抽样信号的频谱没有混叠现象;当不满足F s≥2f m 条件时,抽样信号的频谱发生了混叠,即图5-2的第二行F s<2f m的频谱图,,在f m=5f0的围,频谱出现了镜像对称的部分。
数字信号处理上机作业 学院:电子工程学院 班级:021215 组员:
实验一:信号、系统及系统响应 1、实验目的 (1) 熟悉连续信号经理想采样前后的频谱变化关系,加深对时域采样定理的理解。 (2) 熟悉时域离散系统的时域特性。 (3) 利用卷积方法观察分析系统的时域特性。 (4) 掌握序列傅里叶变换的计算机实现方法,利用序列的傅里叶变换对连续信号、离散信号及系统响应进行频域分析。 2、实验原理与方法 (1) 时域采样。 (2) LTI系统的输入输出关系。 3、实验内容及步骤 (1) 认真复习采样理论、离散信号与系统、线性卷积、序列的傅里叶变换及性质等有关内容,阅读本实验原理与方法。 (2) 编制实验用主程序及相应子程序。 ①信号产生子程序,用于产生实验中要用到的下列信号序列: a. xa(t)=A*e^-at *sin(Ω0t)u(t) b. 单位脉冲序列:xb(n)=δ(n) c. 矩形序列: xc(n)=RN(n), N=10 ②系统单位脉冲响应序列产生子程序。本实验要用到两种FIR系统。 a. ha(n)=R10(n); b. hb(n)=δ(n)+2.5δ(n-1)+2.5δ(n-2)+δ(n-3) ③有限长序列线性卷积子程序 用于完成两个给定长度的序列的卷积。可以直接调用MATLAB语言中的卷积函数conv。 conv 用于两个有限长度序列的卷积,它假定两个序列都从n=0 开始。调用格式如下: y=conv (x, h) 4、实验结果分析 ①分析采样序列的特性。 a. 取采样频率fs=1 kHz,,即T=1 ms。 b. 改变采样频率,fs=300 Hz,观察|X(e^jω)|的变化,并做记录(打印曲线);进一步降低采样频率,fs=200 Hz,观察频谱混叠是否明显存在,说明原因,并记录(打印)这时的|X(e^j ω)|曲线。 程序代码如下: close all;clear all;clc; A=50; a=50*sqrt(2)*pi; m=50*sqrt(2)*pi; fs1=1000; fs2=300; fs3=200; T1=1/fs1; T2=1/fs2; T3=1/fs3; N=100;
补充内容:模拟调制系统的MATLAB 仿真 1.抽样定理 为了用实验的手段对连续信号分析,需要先对信号进行抽样(时间上的离散化),把连续数据转变为离散数据分析。抽样(时间离散化)是模拟信号数字化的第一步。 Nyquist 抽样定律:要无失真地恢复出抽样前的信号,要求抽样频率要大于等于两倍基带信号带宽。 抽样定理建立了模拟信号和离散信号之间的关系,在Matlab 中对模拟信号的实验仿真都是通过先抽样,转变成离散信号,然后用该离散信号近似替代原来的模拟信号进行分析的。 【例1】用图形表示DSB 调制波形)4cos()2cos(t t y ππ= 及其包络线。 clf %%计算抽样时间间隔 fh=1;%%调制信号带宽(Hz) fs=100*fh;%%一般选取的抽样频率要远大于基带信号频率,即抽样时间间隔要尽可能短。 ts=1/fs; %%根据抽样时间间隔进行抽样,并计算出信号和包络 t=(0:ts:pi/2)';%抽样时间间隔要足够小,要满足抽样定理。 envelop=cos(2*pi*t);%%DSB 信号包络 y=cos(2*pi*t).*cos(4*pi*t);%已调信号 %画出已调信号包络线 plot(t,envelop,'r:','LineWidth',3); hold on plot(t,-envelop,'r:','LineWidth',3); %画出已调信号波形 plot(t,y,'b','LineWidth',3); axis([0,pi/2,-1,1])% hold off% xlabel('t'); %写出图例 【例2】用图形表示DSB 调制波形)6cos()2cos(t t y ππ= 及其包络线。 clf %%计算抽样时间间隔 fh=1;%%调制信号带宽(Hz) fs=100*fh;%抽样时间间隔要足够小,要满足抽样定理。 ts=1/fs; %%根据抽样时间间隔进行抽样
数字信号处理作业 哈尔滨工业大学 2006.10
DFT 习题 1. 如果)(~n x 是一个周期为N 的周期序列,那么它也是周期为N 2的周期序列。把)(~ n x 看作周期为N 的周期序列,令)(~ 1k X 表示)(~n x 的离散傅里叶级数之系数,再把)(~ n x 看作周期为N 2的周期序列,再令)(~ 2k X 表示)(~n x 的离散傅里叶级数之系数。当然,)(~ 1k X 是周期性的,周期为N ,而)(~ 2k X 也是周期性的,周期为N 2。试利用)(~ 1k X 确定)(~ 2k X 。(76-4)
2. 研究两个周期序列)(~ n x 和)(~ n y 。)(~ n x 具有周期N ,而)(~ n y 具有周期M 。序列 )(~n w 定义为)()()(~ ~~n y n x n w +=。 a. 证明)(~ n w 是周期性的,周期为MN 。 b. 由于)(~n x 的周期为N ,其离散傅里叶级数之系数)(~ k X 的周期也是N 。类似地, 由于)(~n y 的周期为M ,其离散傅里叶级数之系数)(~k Y 的周期也是M 。)(~ n w 的离散傅里叶级数之系数)(~ k W 的周期为MN 。试利用)(~ k X 和)(~ k Y 求)(~ k W 。(76-5)
3. 计算下列各有限长度序列DFT (假设长度为N ): a. )()(n n x δ= b .N n n n n x <<-=000)()(δ c .10)(-≤≤=N n a n x n (78-7) 4. 欲作频谱分析的模拟数据以10千赫速率被取样,且计算了1024个取样的离散傅里叶变换。试求频谱取样之间的频率间隔,并证明你的回答。(79 -10)
仿真作业 姓名:李亮 学号:S130101083
4.17程序 clc; clear; for i=1:500 sigma_v1=0.27; b(1)=-0.8458; b(2)=0.9458; a(1)=-(b(1)+b(2)); a(2)=b(1)*b(2); datlen=500; rand('state',sum(100*clock)); s=sqrt(sigma_v1)*randn(datlen,1); x=filter(1,[1,a],s); %% sigma_v2=0.1; u=x+sqrt(sigma_v2)*randn(datlen,1); d=filter(1,[1,-b(1)],s); %% w0=[1;0]; w=w0; M=length(w0); N=length(u); mu=0.005; for n=M:N ui=u(n:-1:n-M+1); y(n)=w'*ui; e(n)=d(n)-y(n); w=w+mu.*conj(e(n)).*ui; w1(n)=w(1); w2(n)=w(2); ee(:,i)=mean(e.^2,2); end end ep=mean(ee'); plot(ep); xlabel('迭代次数');ylabel('MSE');title('学习曲线'); plot(w1); hold; plot(w2); 仿真结果:
步长0.015仿真结果 0.10.20.30.4 0.50.60.7迭代次数 M S E 学习曲线
步长0.025仿真结果
步长0.005仿真结果 4.18 程序 data_len = 512; %样本序列的长度 trials = 100; %随机试验的次数 A=zeros(data_len,2);EA=zeros(data_len,1); B=zeros(data_len,2);EB=zeros(data_len,1); for m = 1: trials a1 = -0.975; a2 = 0.95; sigma_v_2 =0.0731; v = sqrt(sigma_v_2) * randn(data_len, 1, trials);%产生v(n) u0 = [0 0]; num = 1; den = [1 a1 a2]; Zi = filtic(num, den, u0); %滤波器的初始条件 u = filter(num, den, v, Zi); %产生样本序列u(n) %(2)用LMS滤波器来估计w1和w2 mu1 = 0.05; mu2 = 0.005; w1 = zeros(2, data_len);
数字信号处理作业-答案
数字信号处理作业
DFT 习题 1. 如果)(~ n x 是一个周期为N 的周期序列,那么它也是周期为N 2的周期序列。把)(~ n x 看作周期为N 的周期序列,令)(~ 1 k X 表示)(~ n x 的离散傅里叶级数之系数,再把)(~ n x 看作周期为N 2的周期序列,再令)(~2 k X 表示)(~ n x 的离散傅里叶级数之系数。当然,)(~ 1 k X 是周期性的,周期为N ,而)(~ 2 k X 也是周期性的,周期为N 2。试利用)(~ 1k X 确定)(~ 2 k X 。(76-4)
2. 研究两个周期序列)(~ n x 和)(~ n y 。)(~ n x 具有周期N ,而)(~ n y 具有周期M 。序列)(~ n w 定义为)()()(~~ ~ n y n x n w +=。 a. 证明)(~ n w 是周期性的,周期为MN 。 b. 由于)(~ n x 的周期为N ,其离散傅里叶级数之系数)(~k X 的周期也是N 。类似地,由于)(~ n y 的周期为M ,其离散傅里叶级数之系数)(~ k Y 的周期也是M 。)(~n w 的离散傅里叶级数之系数)(~ k W 的周期为MN 。试利用)(~k X 和)(~k Y 求)(~ k W 。(76-5)
3. 计算下列各有限长度序列DFT (假设长度为N ): a. )()(n n x δ= b .N n n n n x <<-=0 0)()(δ c .10)(-≤≤=N n a n x n (78-7) 4. 欲作频谱分析的模拟数据以10千赫速率被取样,且计算了1024个取样的离散傅里叶变换。试求频谱取样之间的频率间隔,并证明你的回答。(79 -10)
《数字信号处理Ⅰ》作业 姓名: 学号: 学院: 2012 年春季学期
第一章 时域离散信号和时域离散系统 月 日 一 、判断: 1、数字信号处理和模拟信号处理在方法上是一样的。( ) 2、如果信号的取值和自变量都离散,则称其为模拟信号。( ) 3、如果信号的取值和自变量都离散,则称其为数字信号。( ) 4、时域离散信号就是数字信号。( ) 5、正弦序列都是周期的。( ) 6、序列)n (h )n (x 和的长度分别为N 和M 时,则)n (h )n (x *的长度为N+M 。( ) 7、如果离散系统的单位取样响应绝对可和,则该系统稳定。( ) 8、若满足采样定理,则理想采样信号的频谱是原模拟信号频谱以s Ω(采样频率)为周期进行周期延拓的结果。( ) 9、序列)n (h )n (x 和的元素个数分别为21n n 和,则)n (h )n (x *有(1n n 21-+)个元素。( ) 二、选择 1、R N (n)和u(n)的关系为( ): A. R N (n)=u(n)-u(n-N) B. R N (n)=u(n)+u(n-N) C. R N (n)=u(n)-u(n-N-1) D. R N (n)=u(n)-u(n-N+1) 2、若f(n)和h(n)的长度为别为N 、M ,则f(n)*h(n)的长度为 ( ): A.N+M B.N+M-1 C.N-M D.N-M+1 3、若模拟信号的频率范围为[0,1kHz],对其采样,则奈奎斯特速率为( ): A.4kHz B. 3kHz C.2kHz D.1kHz 4、LTIS 的零状态响应等于激励信号和单位序列响应的( ): A.相乘 B. 相加 C.相减 D.卷积 5、线性系统需满足的条件是( ): A.因果性 B.稳定性 C.齐次性和叠加性 D.时不变性 6、系统y(n)=f(n)+2f(n-1)(初始状态为0)是( ): A. 线性时不变系统 B. 非线性时不变系统 C. 线性时变系统 D. 非线性时变系统
数字信号处理大作业 班级:021231 学号: 姓名: 指导老师:吕雁
一写出奈奎斯特采样率和和信号稀疏采样的学习报告和体会 1、采样定理 在进行A/D信号的转换过程中,当采样频率fs.max大于信号中最高频 率fmax的2倍时(fs.max>2fmax),采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的5~10倍;采样定 理又称奈奎斯特定理。 (1)在时域 频带为F的连续信号 f(t)可用一系列离散的采样值f(t1),f(t1±Δt),f(t1±2Δt),...来表示,只要这些采样点的时间间隔Δt≤1/2F,便可根据各 采样值完全恢复原始信号。 (2)在频域 当时间信号函数f(t)的最高频率分量为fmax时,f(t)的值可由一系列 采样间隔小于或等于1/2fo的采样值来确定,即采样点的重复频率fs ≥2fmax。 2、奈奎斯特采样频率 (1)概述 奈奎斯特采样定理:要使连续信号采样后能够不失真还原,采样频率必须 大于信号最高频率的两倍(即奈奎斯特频率)。 奈奎斯特频率(Nyquist frequency)是离散信号系统采样频率的一半,因哈里·奈奎斯特(Harry Nyquist)或奈奎斯特-香农采样定理得名。采样定理指出,只要离散系统的奈奎斯特频率高于被采样信号的最高频率或带宽,就可 以真实的还原被测信号。反之,会因为频谱混叠而不能真实还原被测信号。 采样定理指出,只要离散系统的奈奎斯特频率高于采样信号的最高频率或 带宽,就可以避免混叠现象。从理论上说,即使奈奎斯特频率恰好大于信号带宽,也足以通过信号的采样重建原信号。但是,重建信号的过程需要以一个低 通滤波器或者带通滤波器将在奈奎斯特频率之上的高频分量全部滤除,同时还 要保证原信号中频率在奈奎斯特频率以下的分量不发生畸变,而这是不可能实 现的。在实际应用中,为了保证抗混叠滤波器的性能,接近奈奎斯特频率的分 量在采样和信号重建的过程中可能会发生畸变。因此信号带宽通常会略小于奈 奎斯特频率,具体的情况要看所使用的滤波器的性能。需要注意的是,奈奎斯 特频率必须严格大于信号包含的最高频率。如果信号中包含的最高频率恰好为
数字信号处理第三章作业 1.(第三章习题3)在图P3-2中表示了两个周期都为6的周期性序列,确定这个两个序列的周期卷积的结果3()x n ,并画出草图。 2.(第三章习题5)如果()x n 是一个具有周期为N 的周期性序列,它也是具有周期为2N 的周期性序列。令~1()X k 表示当()x n 看做是具有周期为N 的周期性序列的DFS 系数。而~2()X k 表示当()x n 看作是具有周期为2N 的周期性序列的DFS 系数。当然~1()X k 是具有周期为N 的周期性序列,而~2()X k 是具有周期为2N 的周期性序列,试根据~1()X k 确定~2()X k 。 3.(第三章习题6) (a )试证明下面列出的周期性序列离散傅里叶级数的对称特性。在证明中,可以利用离散傅里叶级数的定义及任何前面的性质,例如在证明性质③时可以利用性质①和②。 序列 离散傅里叶级数 ① *()x n ~*()X k - ②*()x n - ~*()X k ③Re ()x n ???? ~ e ()X k ④Im ()j x n ???? ~()o X k
(b )根据已在(a )部分证明的性质,证明对于实数周期序列()x n ,离散傅里叶级数的下列对称性质成立。 ①~~Re ()Re ()X k X k ????=-???????? ②~~Im ()Im ()X k X k ????=--???????? ③~~()()X k X k =- ④~~arg ()arg ()X k X k ????=--???????? 4.(第三章习题7)求下列序列的DFT (a) {}11 1-,,,-1 (b) {}1 j 1j -,,,- (c) ()cn 0n 1x n N =≤≤-, (d) 2n ()sin 0n 1x n N N π??=≤≤- ??? , 5.(第三章习题8)计算下列各有限长序列的离散傅立叶变换(假设长度为N ) 1 0)()(0) ()()() ()()(00-≤≤=<<-==N n a n x c N n n n n x b n n x a n δδ 6.(第三章习题9)在图P3-4中表示了一有限长序列)(n x ,画出序列)(1n x 和)(2n x 的草图。(注意:)(1n x 是)(n x 圆周移位两个点) )())(()() ())2(()(442441n R n x n x n R n x n x -=-=
1.设()u n 是离散时间平稳随机过程,证明其功率谱()w 0S ≥。 证明:将()u n 通过冲激响应为()h n 的LTI 离散时间系统,设其频率响应()w H 为 ()001,w -w w 0, w -w w H w ???? 输出随机过程()y n 的功率谱为()()()2y S w H w S w = 输出随机过程()y n 的平均功率为()()()00201 1r 022w w y y w w S w dw S w dw π π π+?-?= =?? 当频率宽度w 0???→时,上式可表示为()()()01 r 00y S w w π =?≥ 由于频率0w 是任意的,所以有()w 0 S ≥ 3、已知:状态方程 )()1,()1()1,()(1n n n n x n n F n x ν-Γ+--=观测方程 )()()()(2n n x n C n z ν+= )()]()([111n Q n n E H =νν )()]()([222n Q n n E H =νν 滤波初值 )]0([)|0(0x E x =ξ } )]]0([)0()]][0([)0({[)0(H x E x x E x E P --= 请简述在此已知条件下卡尔曼滤波算法的递推步骤。 解:步骤1 状态一步预测,即 1 *11)|1(?)1,()|(N n n C n x n n F n x ∈--=--∧ ξξ 步骤2 由观测信号z(n)计算新息过程,即 1*11)|(?)()()|(?)()(M n n C n x n C n z n z n z n ∈-=-=--ξξα 步骤3 一步预测误差自相关矩阵 N N H H C n n n Q n n n n F n P n n F n n P *1)1,()1()1,() 1,()1()1,()1,(∈-Γ--Γ+---=- 步骤4 新息过程自相关矩阵M M H C n Q n C n n P n C n A *2)()()1,()()(∈+-= 步骤5 卡尔曼增益M N H C n A n C n n P n K *1)()()1,()(∈-=- 或 )()()()(1 2n Q n C n P n K H -= 步骤6 状态估计 1*1)()()|(?)|(?N n n C n n K n x n x ∈+=-αξξ 步骤7 状态估计自相关矩阵 N N C n n P n C n K I n P *)1,()]()([)(∈--= 或 )()()()]()()[1,()]()([)(2n K n Q n K n C n K I n n P n C n K I n P H H +---= 步骤8 重复步骤1-7,进行递推滤波计算 4、经典谱估计方法:
1、什么是DSP?简述DSPs的特点?简述DSPs与MCU、FPGA、ARM的区别?学习DSP开发需要哪些知识?学习DSP开发需要构建什么开发环境?(15分) 答:(1)DSP是Digital Signal Processing(数字信号处理的理论和方法)的缩写,同时也是Digital Signal Processor(数字信号处理的可编程微处理器)的缩写。通常流过器件的电压、电流信号都是时间上连续的模拟信号,可以通过A/D器件对连续的模拟信号进行采样,转换成时间上离散的脉冲信号,然后对这些脉冲信号量化、编码,转化成由0和1构成的二进制编码,也就是常说的数字信号。DSP能够对这些数字信号进行变换、滤波等处理,还可以进行各种各样复杂的运算,来实现预期的目标。 (2)DSP既然是特别适合于数学信号处理运算的微处理器,那么根据数字信号处理的要求,DSP芯片一般具有下面所述的主要特点:1)程序空间和数据空间分开,CPU可以同时访问指令和数据; 2)在一个指令周期内可以完成一次乘法和一次加法运算; 3)片内具有快速RAM,通常可以通过独立的数据总线在程序空间和数据空间同时访问; 4)具有低开销和无开销循环及跳转的硬件支持; 5)具有快速的中断处理和硬件I/O支持; 6)可以并行执行多个操作; 7)支持流水线操作,使得取址、译码和执行等操作可以重复执行。(3)DSP采用的是哈佛结构,数据空间和存储空间是分开的,通过
独立的数据总线在数据空间和程序空间同时访问。而MCU采用的是冯·诺依曼结构,数据空间和存储空间共用一个存储器空间,通过一组总线(地址总线和数据总线)连接到CPU)。很显然,在运算处理能力上,MCU不如DSP;但是MCU价格便宜,在对性能要求不是很高的情况下,还是很具有优势的。 ARM是Advanced RISC(精简指令集)Machines的缩写是面向低运算市场的RISC微处理器。ARM具有比较强的事务管理功能,适合用来跑跑界面、操作系统等,其优势主要体现在控制方面,像手持设备90%左右的市场份额均被其占有。而DSP的优势是其强大的数据处理能力和较高的运算速度,例如加密/解密、调制/解调等。 FPGA是Field Programmable Gate Array(现场可编程门阵列)的缩写,它是在PAL、GAL、PLD等可编程器件的基础上进一步发展的产物,是专用集成电路中集成度最高的一种。FPGA采用了逻辑单元阵列LCA(Logical Cell Array)的概念,内部包括了可配置逻辑模块CLB、输入/输出模块IOB、内部连线三个部分。用户可以对FPGA内部的逻辑模块和I/O模块进行重置配置,已实现用户自己的逻辑。它还具有静态可重复编程和动态在系统重构的特性,使得硬件的功能可以像软件一样通过编程来修改。使用FPGA来开发数字电路,可以大大缩短设计时间,减少PCB面积,提高系统的可靠性;同时FPGA可以用VHDL或Verilog HDL来编程,灵活性强。由于FPGA能够进行编程、除错、再编程和重复操作,因此可以充分地进行设计开发和验证。当电路有少量改动时,更能显示出FPGA的优势,其现场编程能力可
仿真题7.17 现有一个在二维平面内运动的目标,它从(60000m,40000m )处,以 (-172m/s,246m/s )的速度出发。在400s 的运动过程中,目标运动速率保持为300m/s ,并在56~105s,182~245s,285~314s 和348~379s 期间分别以1g,-1.5g,3g 和-2.5g(g=9.8m/2s )的转弯速率进行机动,其余时间段则进行匀速运动。系统在两个方向的观测噪声标准差为m y x 100==σσ。采用IMM 算法实现对该目标的跟踪,其中的模型集合由具有不同转弯速率的协同转弯模型构成。定义状态向量由目标在各方向的位置和速度分量构成,即 ()()()[] T y x n v n y n v n x n x )()(= 在协同转弯模型中,状态转移矩阵及状态噪声输入矩阵分别为 ()()()??????? ?????????T T T T -T -T T --T =-ωωωωωωωωωωωωωcos 0sin 0)sin(1) cos(10)sin(0cos 0)cos(10)sin(1)1,(n n F ()?????? ????????T T T T =-Γ2/00002/1,22n n 其中,ω为转弯速率,T 为采样周期。模型集合由7个协同转弯模型组成,转弯速率分别为 s s s s s s s /6.5,/74.3,/87.1,/0,/87.1,/74.3,/6.57654321 ====-=-=-=ωωωωωωω。转速0ω对应模型的系统状态噪声标准差为1.8m/2s ,其余模型的系统状态噪声标准差为2.5m/2s 。模型初始概率为{0.03,0.03,0.03,0.92,0.03,0.03,0.03},转移概率矩阵为 ?????????? ????????????=0.90.1000000.10.80.10000 00.10.80.1000000.10.80.1000000.10.80.1000000.10.80.1000000.10.9π 请给出: (1)目标的真实运动轨迹。
现代数字信号处理仿真作业
第三章仿真作业3.17 (1)代码 clear; N=32; m=[-N+1:N-1]; noise=(randn(1,N)+j*randn(1,N))/sqrt(2); f1=0.15; f2=0.17; f3=0.26; SNR1=30; SNR2=30; SNR3=27; A1=10^(SNR1/20); A2=10^(SNR2/20); A3=10^(SNR3/20); signal1=A1*exp(j*2*pi*f1*(0:N-1)); signal2=A2*exp(j*2*pi*f2*(0:N-1)); signal3=A3*exp(j*2*pi*f3*(0:N-1)); un=signal1+signal2+signal3+noise; uk=fft(un,2*N); sk=(1/N) *abs(uk).^2; r0=ifft(sk); r1=[r0(N+2:2*N),r0(1:N)]; r=xcorr(un,N-1,'biased'); figure subplot(2,2,1) stem(m,real(r1)); xlabel('m'); ylabel('FFT估计r1实部'); subplot(2,2,2) stem(m,imag(r1)); xlabel('m'); ylabel('FFT估计r1虚部'); subplot(2,2,3) stem(m,real(r)); xlabel('m'); ylabel('平均估计r实部'); subplot(2,2,4) stem(m,imag(r)); xlabel('m'); ylabel('平均估计r虚部'); 仿真结果