
3.(2012?岳阳)如图,一次函数y1=x+1的图象与反比例函数y2=
2
x
的图象交于A、B两点,过点作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO、BO,下列说法正确的是()
A.点A和点B关于原点对称
B.当x<1时,y1>y2
C.S△AOC=S△BOD
D.当x>0时,y1、y2都随x的增大而增大
.(2011?湖州)如图,已知A、B是反比例函数y=
k
x
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C (图中“→”所示路线)匀速运动,终点为C.过P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为()
A.B.C.D.
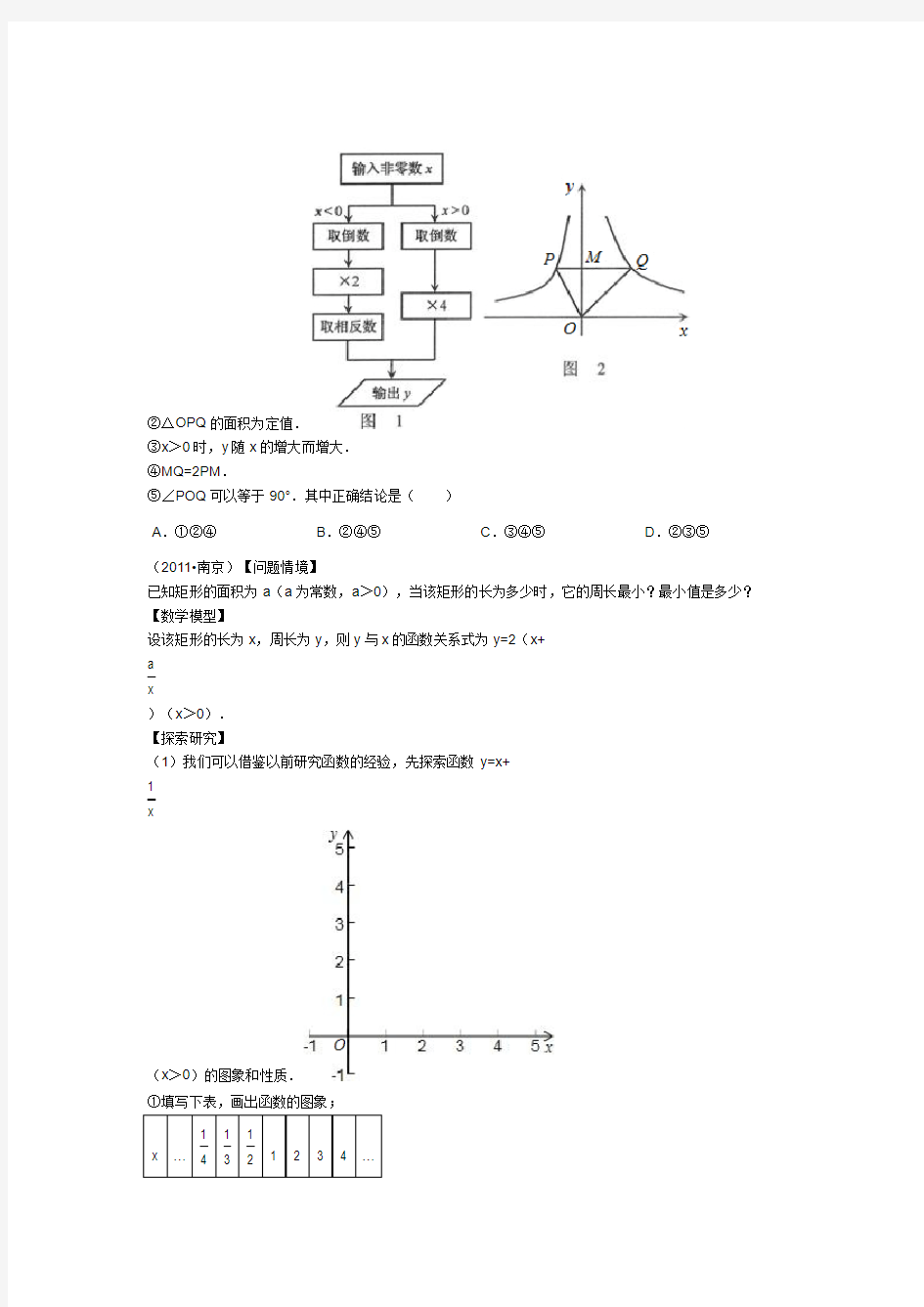
.(2011?河北)根据图1所示的程序,得到了y与x的函数图象,如图2.若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.则以下结论:
①x<0时,y=
2
x
②△OPQ的面积为定值.
③x>0时,y随x的增大而增大.
④MQ=2PM.
⑤∠POQ可以等于90°.其中正确结论是()
A.①②④B.②④⑤C.③④⑤D.②③⑤
(2011?南京)【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?【数学模型】
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+
a
x
)(x>0).
【探索研究】
(1)我们可以借鉴以前研究函数的经验,先探索函数y=x+
1
x
(x>0)的图象和性质.
①填写下表,画出函数的图象;
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数y=x+
1
x
(x>0)的最小值.
【解决问题】
(2)用上述方法解决“问题情境”中问题如图,已知直线y=kx+b(k≠0)经过点A(-1,0),且与双曲线y=
k
x
(x<0)交于点B(-2,1),点C是x轴上方直线y=kx+b(k≠0)
上一点,过点C作x轴的平行线,分别交双曲线y=
k
x
(x<0)和y=-
k
x
(x>0)于点D,E两点.
(1)填空:k=
,b=
.
(2)若点C在直线y=2上,判断线段BD和线段AE的位置关系和数量关系,并说明理由.(2012?淄博)如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).
(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线y=-
1
2
x+b过点D,与线段AB相交于点F,求点F的坐标;
(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.出答案.
.
(2012?莆田)如图,一次函数y=k1x+b的图象过点A(0,3),且与反比例函数y=
k2
x
(x>O)的图象相交于B、C两点.
(1)若B(1,2),求k1?k2的值;
(2)若AB=BC,则k1?k2的值是否为定值?若是,请求出该定值;若不是,请说明理由
3.2 与几何图形结合3.2.1 与等腰三角形结合1、如图,直线y=3x+3交x 轴于A 点,交y 轴于B 点,过A 、B 两点的抛物线交 x 轴于另 一点C (3,0). ⑴求抛物线的解析式 ; ⑵在抛物线的对称轴上是否存在点Q ,使△ABQ 是等腰三角形?若存在,求出符合条件的 Q 点坐标;若不存在,请说明理由 2、如图,已知直线y=x 与交于A 、B 两点. (1)求交点A 、B 的坐标;(2)记一次函数y=x 的函数值为y 1,二次函数 的函数值为y 2.若y 1>y 2,求x 的 取值范围; (3)在该抛物线上存在几个点,使得每个点与AB 构成的三角形为等腰三角形?并求出不 少于3个满足条件的点 P 的坐标. y =x 2 y =x 2
3、如图,已知二次函数的图象经过点A (3,3)、B (4,0)和原点O 。P 为二次函数图象 上的一个动点,过点 P 作x 轴的垂线,垂足为 D (m ,0),并与直线OA 交于点C . (1)求出二次函数的解析式; (2)当点P 在直线OA 的上方时,求线段PC 的最大值; (3)当m >0时,探索是否存在点P ,使得△PCO 为等腰三角形,如果存在,求出 P 的坐 标;如果不存在,请说明理由. 3.2.2 与直角三角形结合1、二次函数的图象的一部分如图所示.已知它的顶点 M 在第二象限,且经 过点A(1,0)和点B(0,l).(1)试求,所满足的关系式;(2)设此二次函数的图象与x 轴的另一个交点为 C ,当△AMC 的面积为△ABC 面积的 倍时,求a 的值;(3)是否存在实数a ,使得△ABC 为直角三角形.若存在,请求出 a 的值;若不存在,请说 明理由. 2 y ax bx c a b 5 4
D C B A 几何图形中的函数问题 1如图,在梯形ABCD 中,AB ∥CD . (1)如果∠A =?50,∠B =?80,求证:AB CD BC =+. (2)如果AB CD BC =+,设∠A =?x ,∠B =?y ,那么y 关于x 的函数关系式是_______. 2.如图,P 是矩形ABCD 的边CD 上的一个动点,且P 不与C 、D 重合,BQ ⊥AP 于点Q ,已知AD=6cm,AB=8cm ,设AP=x(cm),BQ=y(cm). (1)求y 与x 之间的函数解析式并求自变量x 的取值范围; (2)是否存在点P ,使BQ=2AP 。若存在,求出AP 的长;若不存在,说明理由。 3.如图,矩形EFGH 内接与△ABC ,AD ⊥BC 与点D ,交EH 于点M ,BC=10cm , AD=8cm , 设EF=x cm ,EH=y cm ,矩形EFGH 的面积为S cm2, ①分别求出y 与x ,及S 与x 的函数关系式,写出x 的取值范围; ②若矩形EFGH 为正方形,求正方形的边长; ③ x 取何值时,矩形EFGH 的面积最大。 A B D A B C D E F M H G
5.如图,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=x, CE=y (l )如果∠BAC=30°,∠DAE=l05°,试确定y 与x 之间的函数关系式; (2)如果∠BAC=α,∠DAE=β,当α, β满足怎样的关系时,(l )中y 与x 之间的函数关系式还成立?试说明理由. 6.已知:在矩形ABCD 中,AB =10,BC =12,四边形EFGH 的三个顶点E 、F 、H 分别在 矩形ABCD 边AB 、BC 、DA 上,AE =2. (1)如图①,当四边形EFGH 为正方形时,求△GFC 的面积;(5分) (2)如图②,当四边形EFGH 为菱形,且BF = a 时,求△GFC 的面积(用含a 的代数式表示); D C A B E F D C A B E F H G
3.(2012?岳阳)如图,一次函数y1=x+1的图象与反比例函数y2= 2 x 的图象交于A、B两点,过点作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO、BO,下列说法正确的是() A.点A和点B关于原点对称 B.当x<1时,y1>y2 C.S△AOC=S△BOD D.当x>0时,y1、y2都随x的增大而增大 .(2011?湖州)如图,已知A、B是反比例函数y= k x (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C (图中“→”所示路线)匀速运动,终点为C.过P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为() A.B.C.D. .(2011?河北)根据图1所示的程序,得到了y与x的函数图象,如图2.若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.则以下结论: ①x<0时,y= 2 x
②△OPQ的面积为定值. ③x>0时,y随x的增大而增大. ④MQ=2PM. ⑤∠POQ可以等于90°.其中正确结论是() A.①②④B.②④⑤C.③④⑤D.②③⑤ (2011?南京)【问题情境】 已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?【数学模型】 设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+ a x )(x>0). 【探索研究】 (1)我们可以借鉴以前研究函数的经验,先探索函数y=x+ 1 x (x>0)的图象和性质. ①填写下表,画出函数的图象;
中考数学重难点专题讲座 第八讲 动态几何与函数问题 【前言】 在第三讲中我们已经研究了动态几何问题的一般思路,但是那时候没有对其中夹杂的函数问题展开来分析。整体说来,代几综合题大概有两个侧重,第一个是侧重几何方面,利用几何图形的性质结合代数知识来考察。而另一个则是侧重代数方面,几何性质只是一个引入点,更多的考察了考生的计算功夫。但是这两种侧重也没有很严格的分野,很多题型都很类似。所以相比昨天第七讲的问题,这一讲将重点放在了对函数,方程的应用上。其中通过图中已给几何图形构建函数是重点考察对象。不过从近年北京中考的趋势上看,要求所构建的函数为很复杂的二次函数可能性略小,大多是一个较为简单的函数式,体现了中考数学的考试说明当中“减少复杂性”“增大灵活性”的主体思想。但是这也不能放松,所以笔者也选择了一些较有代表性的复杂计算题仅供参考。 【例1】 如图①所示,直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l .将直线l 平移,平移后的直线l 与x 轴交于点D ,与y 轴交于点E. (1)将直线l 向右平移,设平移距离CD 为t (t≥0),直角梯形OABC 被直线l 扫过的面积(图中阴影部份)为s ,s 关于t 的函数图象如图②所示,OM 为线段,MN 为抛物线的一部分,NQ 为射线,且NQ 平行于x 轴,N 点横坐标为4,求梯形上底AB 的长及直角梯形OABC 的面积. (2)当24t <<时,求S 关于t 的函数解析式. 【思路分析】本题虽然不难,但是非常考验考生对于函数图像的理解。很多考生看到图二
的函数图像没有数学感觉,反应不上来那个M 点是何含义,于是无从下手。其实M 点就表示当平移距离为2的时候整个阴影部分面积为8,相对的,N 点表示移动距离超过4之后阴影部分面积就不动了。脑中模拟一下就能想到阴影面积固定就是当D 移动过了0点的时候.所以根据这么几种情况去作答就可以了。第二问建立函数式则需要看出当24t <<时,阴影部分面积就是整个梯形面积减去△ODE 的面积,于是根据这个构造函数式即可。动态几何连带函数的问题往往需要找出图形的移动与函数的变化之间的对应关系,然后利用对应关系去分段求解。 【解】 (1)由图(2)知,M 点的坐标是(2,8) ∴由此判断:24AB OA ==, ; ∵N 点的横坐标是4,NQ 是平行于x 轴的射线, ∴4CO = ∴直角梯形OABC 的面积为: ()()112441222 AB OC OA +?=+?=..... (3分) (2)当24t <<时, 阴影部分的面积=直角梯形OABC 的面积-ODE ?的面积 (基本上实际考试中碰到这种求怪异图形面积的都要先想是不是和题中所给特殊图形有割补关系) ∴1122S OD OE =-? ∵142 OD OD t OE ==-, ∴()24OE t =- . ∴()()()21122441242 S t t t =-?-?-=-- 284S t t =-+-. 【例2】 已知:在矩形AOBC 中,4OB =,3OA =.分别以OB OA ,所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是边BC 上的一个动点(不与B C ,重合),过F 点的反比例函数(0)k y k x =>的图象与AC 边交于点E . (1)求证:AOE △与BOF △的面积相等;
反比例函数与几何综合(讲义) 一、知识点睛 反比例函数与几何综合的处理思路 1. 从关键点入手.通过关键点坐标和横平竖直线段长的互相转化,可将函数特 征与几何特征综合在一起进行研究. 2. 对函数特征和几何特征进行转化、组合,列方程求解.若借助反比例函数模 型,能快速将函数特征转化为几何特征. 与反比例函数相关的几个模型,在解题时可以考虑调用. ① 结论:2||ABO ABCO S S k ==△矩形 结论:OCD ABCD S S =△梯形 ② 结论:AB =CD ③
结论:BD∥CE 二、精讲精练 1.如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴 上, 1 4 OA OB =,函数 9 y x =-的图象与线段AB交于点M.若AM=BM,则直线 AB的解析式为_________. 2. 的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是_________.
3. 正方形A 1B 1P 1P 2的顶点P 1,P 2在反比例函数x y 2 = (0x >)的图象上,顶点A 1,B 1分别在x 轴、y 轴的正半轴上,再在其右侧作正方形P 2P 3A 2B 2,顶点P 3在反比例函数x y 2 = (0x >)的图象上,顶点A 2在x 轴的正半轴上,则点P 3的坐标为_________.
4.如图,已知动点A在函数 4 y x =(0 x>)的图象上,AB x ⊥轴于点B, AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴、y轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积为_________.
1.如图,已知抛物线2 1y x =-与x 轴交于A 、B 两点,与y 轴交于点C . (1)求A 、B 、C 三点的坐标; (2)过点A 作AP ∥CB 交抛物线于点P ,求四边形ACBP 的面积; (3)在x 轴上方的抛物线上是否存在一点M ,过M 作MG ⊥x 轴于点G ,使以A 、M 、G 三点为顶点的三角形与?PCA 相似.若存在,请求出M 点的坐标;否则,请说明理由. 解:(1)令0y =,得2 10x -= 解得1x =± 令0x =,得1y =- ∴ A (1,0)- B (1,0) C (0,1)- ……………………3分 (2)∵O A =O B =O C =1 ∴∠BAC =∠AC O=∠BC O= 45 ∵A P ∥CB , ∴∠P AB = 45 过点P 作P E ⊥x 轴于E ,则?A P E 为等腰直角三角形 令O E =a ,则P E =1a + ∴P (,1)a a + ∵点P 在抛物线21y x =-上 ∴2 11a a +=- 解得12a =,21a =-(不合题意,舍去) ∴P E =3……………………………………………………………………………5分 ∴四边形ACB P 的面积S =12AB ?O C +12AB ?P E =11 2123422 ??+??=………………………………6分 (3). 假设存在 ∵∠P AB =∠BAC =45 ∴P A ⊥AC ∵MG ⊥x 轴于点G , ∴∠MG A =∠P AC =90 在Rt △A O C 中,O A =O C =1 ∴AC =2 在Rt △P AE 中,AE =P E =3 ∴A P= 32 ………8分 设M 点的横坐标为m ,则M 2 (,1)m m - ①点M 在y 轴左侧时,则1m <- (ⅰ) 当?A MG ∽?P CA 时,有 AG PA =MG CA ∵A G=1m --,MG=2 1m -即2322 = 解得11m =-(舍去) 23m =(舍去)………9分 G M C B y P A o x
几何图形中的动态问题 ★1.如图,在矩形ABCD中,点E在BC边上,动点P 以2厘米/秒的速度从点A出发,沿△AED的边按照A→E→D→A的顺序运动一周.设点P从点A出发经x(x>0)秒后,△ABP的面积是y. (1)若AB=8cm,BE=6cm,当点P在线段AE上时,求y关于x的函数表达式; (2)已知点E是BC的中点,当点P在线段ED上时,y=12 5x;当点P在线段AD上时,y=32-4x.求y关于x的函数表达式. 第1题图 解:(1)∵四边形ABCD是矩形,∴∠ABE=90°, 又∵AB=8cm,BE=6cm,
∴AE=AB2+BE2=82+62=10厘米,如解图①,过点B作BH⊥AE于点H, 第1题解图① ∵S△ABE=1 2AE·BH=1 2AB·BE, ∴BH=24 5cm,又∵AP=2x, ∴y=1 2AP·BH=24 5x(0 ∴AE =DE , ∵y =12 5x (P 在ED 上), y =32-4x (P 在AD 上), 当点P 运动至点D 时,可联立得,?????y =125x y =32-4x , 解得x =5, ∴AE +ED =2x =10, ∴AE =ED =5cm , 当点P 运动一周回到点A 时,y =0, ∴y =32-4x =0, 解得x =8, ∴AE +DE +AD =16, ∴AD =BC =6cm ,∴BE =3cm , 在Rt △ABE 中, AB = AE 2-BE 2=4cm , 如解图②,过点B 作BN ⊥AE 于N ,则BN =12 5cm , 反比例函数与几何综合(讲义) ?课前预习 前期学习一次函数与几何综合问题时,解决思路是将坐标、几何图形和一次函数综合起来分析、转化.如:坐标与线段长互转,由坐标求解表达式,根据函数表达式计算坐标等,请尝试解决下列问题,并体会整个解决问题的过程: 如图,已知直线l1:y =2 x + 8 与直线l2:y=-2x+16 相交于点 3 3 C,直线l1,l2 分别交x 轴于A,B 两点,矩形DEFG 的顶点D,E 分别在l1,l2 上,顶点F,G 都在x 轴上,且点G 与点B 重合,那么S 矩形DEFG:S△ABC = . 解决一次函数与几何综合问题的核心在于:找坐标,转线段长,借助几何或函数特征建等式求解. 1 ?知识点睛 反比例函数与几何综合的处理思路: 1 .从关键点入手.“关键点”是信息汇聚点,通常是和的.通过和 的互相转化可将与综合在一起进行研究. 2.梳理题干中的函数和几何信息,依次转化. 3.借助或列方程求解. 与反比例函数相关的几个结论,在解题时可以考虑调用. 结论:S 矩形ABCO = 2S △ABO =| k | 结论:S △OCD =S 梯形ABCD 结论:AB=CD 结论:BD∥CE 函数几何特征常见转化作法: 1.函数→坐标→几何 ①借助表达式设出点坐标; ②将点坐标转化为横平竖直线段长; ③结合几何特征利用线段长列方程. 2.几何→坐标→函数 ①研究几何特征,考虑线段间关系; ②通过设线段长进而表达点坐标; ③将点坐标代入函数表达式列方程.若(x1,y1),(x2,y2)是同一反比例函 数上的点,则: ①当x1,y1,x2,y2 都用同一字母表达出来时,往往利用x1y1=x2y2=k 列方程求解. ②当两点的横坐标有比例关系时,对应的纵坐标也有比例关系.这样的比例关系常通过横平竖直的线段放在相似三角形中使用. 如: x 1 = y 2 x 2 y 1 专题 反比例函数与几何图形综合题 反比例函数与三角形 1.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A ,B 两点,与x 轴交于点C ,与y 轴交于点D ,点B 的坐标 是(m ,-4),连接AO ,AO =5,sin ∠AOC =3 5. (1)求反比例函数的解析式; (2)连接OB ,求△AOB 的面积. 分析:(1)过点A 作AE ⊥x 轴于点E ,通过解直角三角形求出线段AE ,OE 的长度,得出点A 的坐标,即可求出反比例函数解析式;(2)先求出点B 的坐标,再求直线AB 的解析式,从而可求出点C 的坐标,再利用三角形的面积公式即可得出结论. 解:(1)过点A 作AE ⊥x 轴于点E ,设反比例函数解析式为y =k x .∵AE ⊥x 轴,∴∠AEO =90°.在Rt △AEO 中,AO =5,sin ∠AOC =3 5,∴AE =AO·sin ∠AOC =3,OE =AO 2-AE 2=4,∴点A 的坐标为(-4,3),可求反比例函数解析式 为y =-12 x (2)易求B(3,-4),可求直线AB 的解析式为y =-x -1.令一次函数y =-x -1中y =0,则0=-x -1,解得x =-1,∴C(-1,0),∴S △AOB =1 2OC·(y A -y B )=12×1×[3-(-4)]=72 反比例函数与四边形 2. (2016·恩施)如图,直角三角板ABC 放在平面直角坐标系中,直角边AB 垂直于x 轴,垂足为点Q ,已知∠ACB =60°,点A ,C ,P 均在反比例函数y =43 x 的图象上,分别作PF ⊥x 轴于点F ,AD ⊥y 轴于点D ,延长DA ,FP 交于点E ,且点P 为EF 的中点. (1)求点B 的坐标; (2)求四边形AOPE 的面积. 分析:(1)设点A(a ,b),则tan 60°=b a =3,b =43 a ,联立可求点A 的坐标,从而得出点C ,B 的坐标; (2)先求出AQ ,PF 的长,从而可求点P 的坐标和S △OPF ,再求出S 矩形DEFO ,根据S 四边形AOPE =S 矩形DEFO -S △AOD -S △OPF ,代入计算即可. 解:(1)∵∠ACB =60°,∴∠AOQ =60°,∴tan 60°=AQ OQ =3,设点A(a , b),则? ??b a =3, b =43a , 解得?????a =2,b =23或?????a =-2, b =-23(不合题意,舍去),∴点A 的坐标是 (2,23),∴点C 的坐标是(-2,-23),∴点B 的坐标是(2,-23) (2)∵点A 的坐标是(2,23),∴AQ =23,∴EF =AQ =23,∵点P 为EF 的中点,∴PF =3,设点P 的坐标是(m ,n),则n =3,∵点P 在反比例函数y =43x 的图象上,∴3=43m ,S △OPF =1 2|43|=23,∴m =4,∴OF =4,∴S 矩形 DEFO =OF·OD =4×23=83,∵点A 在反比例函数y = 43 x 的图象上,∴S △AOD =1 2|43|=23,∴S 四边形AOPE =S 矩形DEFO -S △AOD -S △OPF =83-23-23=4 3 二次函数与几何图形综合题 类型 1 二次函数与相似三角形的存在性问题 1.(2015·昆明西山区一模)如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(4,0),C(0,2) 三点. (1)求这条抛物线的解析式; (2)P 为线段BC 上的一个动点,过P 作PE 垂直于x 轴与抛物线交于点E,设P 点横坐标为m,PE 长度为y,请写出y 与m 的函数关系式,并求出PE 的最大值; (3)D 为抛物线上一动点,是否存在点D 使以A、B、D 为顶点的三角形与△COB 相似?若存在,试求出点D 的坐标;若不存在,请说明理由. 2.(2013·曲靖)如图,在平面直角坐标系xOy 中,直线y=x+4 与坐标轴分别交于A,B 两点,过A,B 两点的抛物线为y=-x2+bx+c.点D 为线段AB 上一动点,过点D 作CD⊥x 轴于点C,交抛物线于点E. (1)求抛物线的解析式; (2)当DE=4 时,求四边形CAEB 的面积; (3)连接BE,是否存在点D,使得△DBE 和△DAC 相似?若存在,求出D 点坐标;若不存在,说明理由. 3.(2015·襄阳)边长为 2 的正方形OABC 在平面直角坐标系中的位置如图所示,点D 是边OA 的中点,连接CD,点E 在第一象限,且DE⊥DC,DE=DC.以直线AB 为对称轴的抛物线过C,E 两点. (1)求抛物线的解析式; (2)点P 从点C 出发,沿射线CB 以每秒 1 个单位长度的速度运动,运动时间为t 秒.过点P 作PF⊥CD 于点F.当t 为何值时,以点P,F,D 为顶点的三角形与△COD 相似? (3)点M 为直线AB 上一动点,点N 为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E 为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由. 类型 2 二次函数与平行四边形的存在性问题 1.(2014·曲靖)如图,抛物线y=ax2+bx+c 与坐标轴分别交于A(-3,0),B(1,0),C(0,3)三点,D 二次函数与几何图形 模式1:平行四边形 分类标准:讨论对角线 例如:请在抛物线上找一点p 使得P C B A 、、、四点构成平行四边形,则可分成以下几种情况 (1)当边AB 是对角线时,那么有BC AP // (2)当边AC 是对角线时,那么有CP AB // (3)当边BC 是对角线时,那么有BP AC // 1、本题满分14分)在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点. (1)求抛物线的解析式; (2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值; (3)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标. 2、如图1,抛物线322 ++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D . (1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴; (2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m . ①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设△BCF 的面积为S ,求S 与m 的函数关系. 模式2:梯形 分类标准:讨论上下底 例如:请在抛物线上找一点p 使得P C B A 、、、四点构成梯形,则可分成以下几种情况 (1)当边AB 是底时,那么有PC AB // (2)当边AC 是底时,那么有BP AC // (3)当边BC 是底时,那么有AP BC // 3、已知,矩形OABC 在平面直角坐标系中位置如图1所示,点A 的坐标为(4,0),点C 的坐标为)20(-,,直线 x y 3 2 -=与边BC 相交于点D . (1)求点D 的坐标; (2)抛物线c bx ax y ++=2 经过点A 、D 、O ,求此抛物线的表达式; (3)在这个抛物线上是否存在点M ,使O 、D 、A 、M 为顶点的四边形是梯形?若存在,请求出所有符合条件的点M 的坐标;若不存在,请说明理由. 代几结合专题:反比例函数与几何图形的综合(选做) ——代几结合,掌握中考风向标 ◆类型一 与三角形的综合 1.(2016·云南中考)位于第一象限的点E 在反比例函数y =k x 的图象上,点F 在x 轴的 正半轴上,O 是坐标原点.若EO =EF ,△EOF 的面积等于2,则k 的值为( ) A .4 B .2 C .1 D .-2 2.(2016·菏泽中考)如图,△OAC 和△BAD 都是等腰直角三角形,∠ACO =∠ADB =90°,反比例函数y =6 x 在第一象限的图象经过点B ,则△OAC 与△BAD 的面积之差S △OAC -S △BAD 为( ) A .36 B .12 C .6 D .3 3.如图,点A 在双曲线y =5x 上,点B 在双曲线y =8 x 上,且AB ∥x 轴,则△OAB 的 面积等于________. 第3题图 第4题图 4.(2016·包头中考)如图,在平面直角坐标系中,点A 在第二象限内,点B 在x 轴上,∠AOB =30°,AB =BO ,反比例函数y =k x (x <0)的图象经过点A ,若S △AOB =3,则k 的值为________. 5.(2016·宁波中考)如图,点A 为函数y =9 x (x >0)图象上一点,连接OA ,交函数y =1 x (x >0)的图象于点B ,点C 是x 轴上一点,且AO =AC ,则△ABC 的面积为________. 第5题图 第6题图 6.★如图,若双曲线y =k x (k >0)与边长为3的等边△AOB (O 为坐标原点)的边OA 、 AB 分别交于C 、D 两点,且OC =2BD ,则k 的值为________. 7.(2016·宁夏中考)如图,Rt △ABO 的顶点O 在坐标原点,点B 在x 轴上,∠ABO =90°,∠AOB =30°,OB =23,反比例函数y =k x (x >0)的图象经过OA 的中点C ,交 AB 于点D . (1)求反比例函数的关系式; (2)连接CD ,求四边形CDBO 的面积. 8.(2016·大庆中考)如图,P 1、P 2是反比例函数y =k x (k >0)在第一象限图象上的两点,点A 1的坐标为(4,0).若△P 1OA 1与△P 2A 1A 2均为等腰直角三角形,其中点P 1、P 2为直角顶点. (1)求反比例函数的解析式; (2)①求P 2的坐标;②根据图象直接写出在第一象限内当x 满足什么条件时,经过点P 1、 P 2的一次函数的函数值大于反比例函数y =k x 的函数值. 二次函数与几何图形综合题 类型 1二次函数与相似三角形的存在性问题 1. (2015 ·明西山区一模昆)如图,已知抛物线y= ax2+bx+ c(a≠0)经过 A(- 1, 0), B(4, 0), C(0 ,2) 三点. (1)求这条抛物线的解析式; (2)P 为线段 BC 上的一个动点,过P 作 PE 垂直于 x 轴与抛物线交于点 E,设 P 点横坐标为 m, PE 长度为 y,请写出 y 与 m 的函数关系式,并求出PE 的最大值; (3)D 为抛物线上一动点,是否存在点 D 使以 A、B、D 为顶点的三角形与△ COB 相似?若存在,试求出点 D 的坐标;若不存在,请说明理由. 2. (2013 ·靖曲 )如图,在平面直角坐标系xOy 中,直线y= x+ 4 与坐标轴分别交于A, B 两点,过A,B 两点的抛物线为y=- x2+ bx+ c.点 D 为线段 AB 上一动点,过点 D 作 CD⊥ x 轴于点 C,交抛物线于点 E. (1)求抛物线的解析式; (2)当 DE= 4 时,求四边形CAEB 的面积; (3)连接 BE,是否存在点 D ,使得△ DBE 和△ DAC 相似?若存在,求出 D 点坐标;若不存在,说明理由. 3.(2015 襄·阳 )边长为 2 的正方形O ABC 在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接 CD ,点 E 在第一象限,且DE⊥ DC , DE =DC.以直线 AB 为对称轴的抛物线过C, E 两点. (1)求抛物线的解析式; (2)点 P 从点 C 出发,沿射线 CB 以每秒 1 个单位长度的速度运动,运动时间为t 秒.过点 P 作 PF ⊥ CD 于点 F .当 t 为何值时,以点P, F ,D 为顶点的三角形与△COD 相似? (3)点 M 为直线 AB 上一动点,点N 为抛物线上一动点,是否存在点M, N,使得以点M,N, D, E 为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由. D C B A 几何图形中的函数问题 1如图,在梯形ABCD 中,AB ∥CD 、 (1)如果∠A =?50,∠B =?80,求证:AB CD BC =+、 (2)如果AB CD BC =+,设∠A =?x ,∠B =?y ,那么y 关于x 的函数关系式就是_______、 2、如图,P 就是矩形ABCD 的边CD 上的一个动点,且P 不与C 、D 重合,BQ ⊥AP 于 点Q,已知AD=6cm,AB=8cm,设AP=x(cm),BQ=y(cm)、 (1)求y 与x 之间的函数解析式并求自变量x 的取值范围; (2)就是否存在点P,使BQ=2AP 。若存在,求出AP 的长;若不存在, 说明理由。 3、如图,矩形EFGH 内接与△ABC,AD ⊥BC 与点D,交EH 于点M,BC=10cm, AD=8cm, 设EF=x cm,EH=y cm ,矩形EFGH 的面积为S cm2, ①分别求出y 与x,及S 与x 的函数关系式,写出x 的取值范围; ②若矩形EFGH 为正方形,求正方形的边长; ③x 取何值时,矩形EFGH 的面积最大。 5.如图,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=x, CE=y (l)如果∠BAC=30°,∠DAE=l05°,试确定y 与x 之间的函数关系式; (2)如果∠BAC=α,∠DAE=β,当α, β满足怎样的关系时,(l)中y 与x 之间的函数关系式还成立?试说明理由. 6、已知:在矩形ABCD 中,AB =10,BC =12,四边形EFGH 的三个顶点E 、F 、H 分别在 矩形ABCD 边AB 、BC 、DA 上,AE =2、 (1)如图①,当四边形EFGH 为正方形时,求△GFC 的面积;(5分) (2)如图②,当四边形EFGH 为菱形,且BF = a 时,求△GFC 的面积 (用含a 的 A B C D P Q A B C D E F M H G 反比例函数常见几何模 型94169 公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08] 反比例函数常见模型 一、知识点回顾 1..反比例函数的图像是双曲线,故也称双曲线y=k x (k≠0).其解析式有三种表示方法:①x k y = (0≠k );②1-=kx y (0≠k );③k xy = 2.反比例函数y=k x (k≠0)的性质 (1)当k>0时?函数图像的两个分支分别在第一,三象限内?在每一象限内,y 随x 的增大而减小. (2)当k<0时?函数图像的两个分支分别在第二,四象限内?在每一象限内,y 随x 的增大而增大. (3)在反比例函数y=k x 中,其解析式变形为xy=k ,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积). (4)若双曲线y=k x 图像上一点(a ,b )满足a ,b 是方程Z 2-4Z -2=0的两根,求双曲线的解析式.由根与系数关系得ab=-2,又ab=k ,∴k=-2,故双曲线的解析式是y= 2x -. (5)由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴,y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势. 二、新知讲解与例题训练 模型一: 如图,点A 为反比例函数x k y =图象上的任意一点,且AB 垂直于x 轴,则有 2||k S OAB = ? 例1:如图ABC Rt ?的锐角顶点是直线y=x+m 与双曲线y= x m 在第一象限的交点,且3=?AOB S ,(1)求m 的值 (2)求ABC ?的面积 变式题 1、如图所示,点1A ,2A ,3A 在x 轴上,且O 1A =21A A =32A A ,分别过 1A ,2A ,3A 作y 轴平行线,与反比例函数y= x 8 (x>0)的图像交于点1B ,2B ,3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为 __________ ---几何图形在二次函数中的存在性问题探解 二次函数是初中数学的重要内容,更是中考的重要考点之一,它以丰富的知识内涵,深远的知识综合,深厚的数学思想,灵活的解题方法,奇趣的知识背景等深深吸引着命题老师,更深刻启迪着每位同学.下面就把几何图形在二次函数中的存在性问题介绍给大家,供学习时借鉴. 一、.三角形的存在性 1.1 等腰三角形的存在性 例1 (2017年淮安)如图1-1,直线y=﹣x+3与x 轴、y 轴分别交于点B 、点C ,经过B 、C 两点的抛物线y=2x +bx+c 与x 轴的另一个交点为A ,顶点为P . (1)求该抛物线的解析式; (2)在该抛物线的对称轴上是否存在点M ,使以C ,P ,M 为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M 的坐标;若不存在,请说明理由; (3)当0<x <3时,在抛物线上求一点E ,使△CBE 的面积有最大值(图1-2、1-3供画图探究). 分析: 第一问考查的是待定系数法确定函数的解析式,思路有几个待定系数,解答时就需要确定几个点的坐标; 第二问探析等腰三角形的存在性,解答时,要做到一先一后,先清楚动点的位置与特点,后对等腰三角形进行科学分类,一是按边分类,一是按角分类; 第三问探求三角形面积的最大值,这是二次函数的看家本领,只需将三角形的面积适当分割,恰当表示,最后将三角形面积最大问题转化为二次函数的最值问题求解即可. 解: (1)因为直线y=﹣x+3与x 轴、y 轴分别交于点B 、点C ,所以B (3,0),C (0,3), 所以{c =39a+3b+c =0,解得{c =3b =4-,所以抛物线解析式为y=2x ﹣4x+3; (2)因为y=2x ﹣4x+3=2(x 2)-﹣1,所以抛物线对称轴为x=2,顶点P (2,﹣1), 设M (2,t ),因为△CPM 为等腰三角形,如图2所示, ①当MC=PC 时,过C 作CQ ⊥对称轴,垂足为Q ,则Q(2,3),所以QP=MQ=3-(-1)=4,所以M 到x 轴的距离8-1=7,所以1M 的坐标(2,7); ②当MP=MC 时,作PC 的垂直平分线交对称轴于点M ,所以222(t+1)2+(t-3)=,解得t=32,所以2M 的坐标(2, 32 ); 专题九 反比例函数与几何图形综合题 反比例函数与三角形 【例1】 (2016·重庆)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A ,B 两点,与x 轴交于点C ,与y 轴交于点D ,点B 的坐标是(m , -4),连接AO ,AO =5,sin ∠AOC =3 5 . (1)求反比例函数的解析式; (2)连接OB ,求△AOB 的面积. 分析:(1)过点A 作AE⊥x 轴于点E ,通过解直角三角形求出线段AE ,OE 的长度,得出点A 的坐标,即可求出反比例函数解析式;(2)先求出点B 的坐标,再求直线AB 的解析式,从而可求出点C 的坐标,再利用三角形的面积公式即可得出结论. 解:(1)过点A 作AE⊥x 轴于点E ,设反比例函数解析式为y =k x .∵AE⊥x 轴,∴∠AEO =90°.在Rt △AEO 中,AO =5,sin ∠AOC =35 ,∴AE =AO·sin ∠AOC =3,OE =AO 2-AE 2 =4, ∴点A 的坐标为(-4,3),可求反比例函数解析式为y =-12 x (2)易求B(3,-4),可求直线AB 的解析式为y =-x -1.令一次函数y =-x -1中y = 0,则0=-x -1,解得x =-1,∴C(-1,0),∴S △AOB =12OC·(y A -y B )=1 2 ×1×[3-(-4)] =72 反比例函数与四边形 【例2】 (2016·恩施)如图,直角三角板ABC 放在平面直角坐标系中,直角边AB 垂 直于x 轴,垂足为点Q ,已知∠ACB =60°,点A ,C ,P 均在反比例函数y =43 x 的图象上, 分别作PF⊥x 轴于点F ,AD ⊥y 轴于点D ,延长DA ,FP 交于点E ,且点P 为EF 的中点. (1)求点B 的坐标; (2)求四边形AOPE 的面积. 分析:(1)设点A(a ,b),则tan 60°=b a =3,b =43 a ,联立可求点A 的坐标,从而 得出点C ,B 的坐标; (2)先求出AQ ,PF 的长,从而可求点P 的坐标和S △OPF ,再求出S 矩形DEFO ,根据S 四边形AOPE =S 矩形DEFO -S △AOD -S △OPF ,代入计算即可. 专训1 反比例函数与几何的综合应用 名师点金:解反比例函数与几何图形的综合题,一般先设出几何图形中的未知数,然后结合函数的图象用含未知数的式子表示出几何图形与图象的交点坐标,再由函数解析式及几何图形的性质写出含未知数及待求字母系数的方程(组),解方程(组)即可得所求几何图形中的未知量或函数解析式中待定字母的值. 反比例函数与三角形的综合 1.如图,一次函数y =kx +b 与反比例函数y =x 6(x>0)的图象交于 A(m,6),B(3,n)两点. (1)求一次函数的解析式; (2)根据图象直接写出使kx +b (第3题) 反比例函数与矩形的综合 4.如图,矩形OABC 的顶点A,C 的坐标分别就是(4,0)与(0,2),反比例函数y =x k (x>0)的图象过对角线的交点P 并且与AB, (第4题) BC 分别交于D,E 两点,连接OD,OE,DE,则△ODE 的面积为________. 5.如图,在平面直角坐标系中,矩形OABC 的对角线OB,AC 相交于点D,且BE ∥AC,AE ∥OB 、 (1)求证:四边形AEBD 就是菱形; (2)如果OA =3,OC =2,求出经过点E 的双曲线对应的函数解析式. (第5题) 反比例函数与菱形的综合 6.如图,在平面直角坐标系中,菱形ABCD 在第一象限内,边BC 与x 轴平行,A,B 两点的纵坐标分别为3,1,反比例函数y =x 3的图象 (第6题) 经过A,B 两点,则菱形ABCD 的面积为( ) A .2 B .4 C .2 D .4 7.如图,在平面直角坐标系中,菱形ABCD 的顶点C 与原点O 重合,点B 在y 轴的正 几何中的函数问题 金汇学校初三数学备课组 教学目标: 以四边形为载体探究几何图形中两个变量的数量关系,了解、掌握在几何图形背景中建立函数解析式常见的方法;研究几何图形的性质,沟通函数与几何的关系,体验函数在几何图形中的应用;进一步感悟和运用数形结合思想、分类讨论思想、方程思想解决综合问题。 教学重点与难点: 探求几何图形中两个变量之间的函数关系,寻找解题规律,并正确写出函数定义域。 教学过程: 问题1:已知正方形ABCD 中,点P 在对角线BD 上,联结PC ,过点P 作PE ⊥PC ,交AB 于点E ,如图1所示。 求证:PE=PC . (学生独立思考并解答,让学生体会随着点P 的运动,变量PE 、 PC 之间的关系) 问题2:如果把条件中的正方形改为梯形ABCD ,其中AD ∥BC , ∠ABC = 90,并设AD =3,AB =4,BC =6,(如图)若将一个直角顶点P 放在对角线BD 上移动,一条直角边过点C ,另一条直角边与腰AB (或AB 思考:图中哪些量在变化? 探究一:当Q 在AB 的上 时试探究PQ 、PC 之间有怎样的数量关系,并证明你的结论; (说明:以问题(1)为铺垫,从几何图形入 手,根据几何图形的特点,运用几何图形的有关 性质,来找到两个变量PQ 、PC 之间的关系。) 探究二、在图2中,联结AP ,且点Q 在线段AB 上时,设点B Q 、之间的距离为x , APQ PBC S y S △△,其中APQ S △表 示APQ △的面积,PBC S △表示PBC △的面积,求y 关于x 的函 数解析式,并写出函数定义域; 说明:(1)解题的关键是用含x 的代数式表示出相关的线段,利 图1 D C B A E P 。 O 反比例函数常见模型 一、知识点回顾 1..反比例函数的图像是双曲线,故也称双曲线y=k x (k≠0).其解析式有三种表示方法:①x k y = (0≠k );②1-=kx y (0≠k );③k xy = 2.反比例函数y=k x (k≠0)的性质 (1)当k>0时?函数图像的两个分支分别在第一,三象限内?在每一象限内,y 随x 的增大而减小. (2)当k<0时?函数图像的两个分支分别在第二,四象限内?在每一象限内,y 随x 的增大而增大. (3)在反比例函数y=k x 中,其解析式变形为xy=k ,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积). (4)若双曲线y=k x 图像上一点(a ,b )满足a ,b 是方程Z 2-4Z -2=0的两根,求双曲线的解析式.由根与系数关系得ab=-2,又ab=k ,∴k=-2,故双曲线的解析式是y= 2 x -. (5)由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴,y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势. 二、新知讲解与例题训练 模型一: 如图,点A 为反比例函数x k y =图象上的任意一点,且AB 垂直于x 轴,则有2| |k S OAB = ? 例1:如图ABC Rt ?的锐角顶点是直线y=x+m 与双曲线y= x m 在第一象限的交点,且3=?AOB S ,(1)求m 的值 (2)求ABC ?的面积 变式题 1、如图所示,点1A ,2A ,3A 在x 轴上,且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线,与反比例函数y=x 8(x>0)的图像交于点1B ,2B ,3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________ 2、 如图,点A 在双曲线1y x =上,点B 在双曲线3 y x = 上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 . 模型二: 如图:点A 、B 是双曲线)0(≠=k x k y 任意不重合的两点,直线AB 交x 轴于M 点,交 y 轴于N 点,再过A 、B 两点分别作y AD ⊥轴于D 点,x BF ⊥轴于F 点,再连结DF 两点,则有:AB DF ||且BM =AN 例2:如图,一次函数y a x b =+的图象与x 轴,y 轴交于A ,B 两 F反比例函数与几何综合(讲义及答案)
专题 反比例函数与几何图形
二次函数与几何图形综合题(可编辑修改word版)
二次函数与几何图形动点问题--答案
反比例函数与几何图形的综合
(完整版)二次函数与几何图形综合题.doc
几何图形中的函数问题
反比例函数常见几何模型94169
-几何图形在二次函数中的存在性问题探解
中考数学总复习 专题九 反比例函数与几何图形综合题试题 新人教版
反比例函数与几何的综合应用及答案
几何中的函数问题(一)
反比例函数常见几何模型