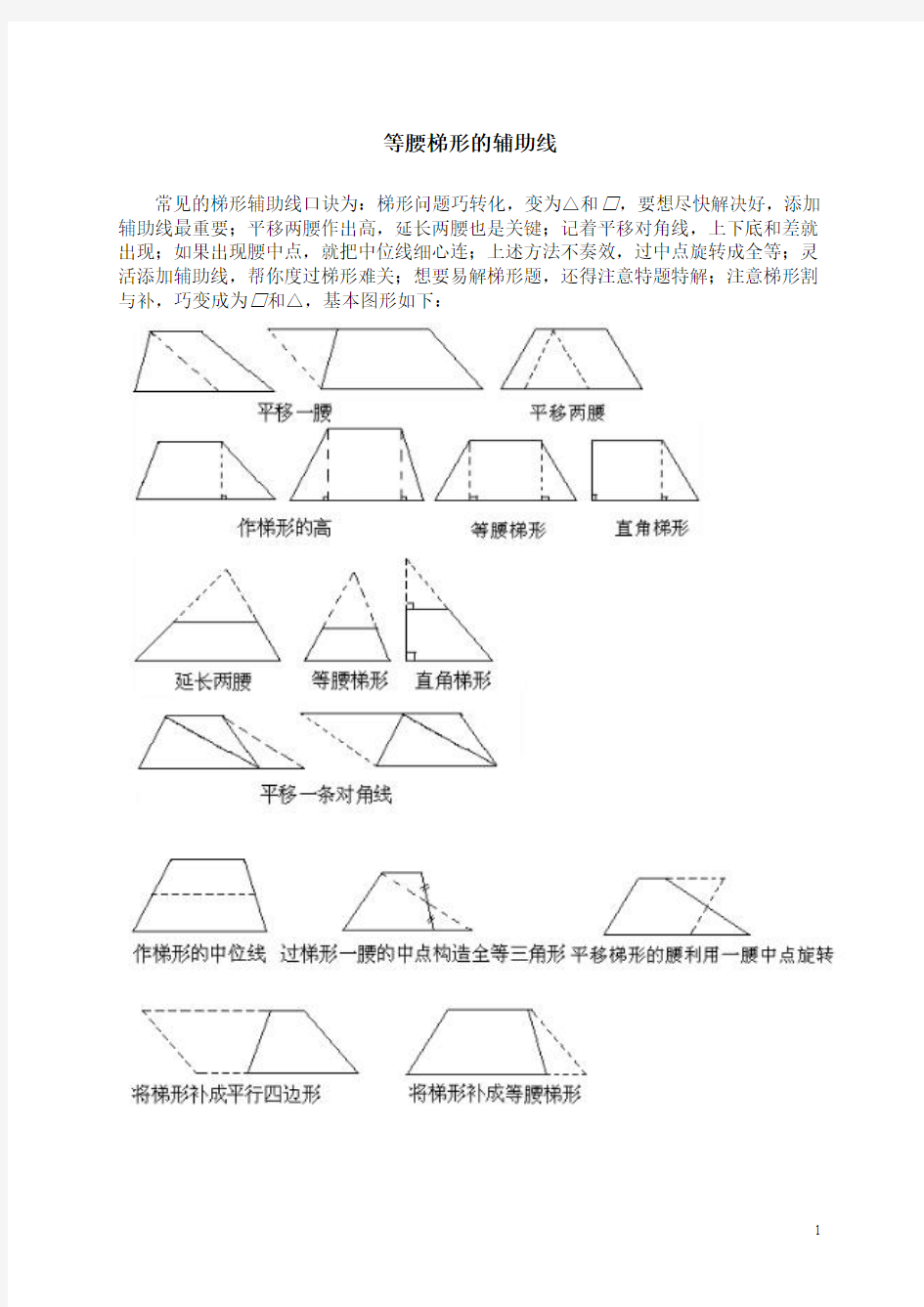

等腰梯形的辅助线
常见的梯形辅助线口诀为:梯形问题巧转化,变为△和□,要想尽快解决好,添加辅助线最重要;平移两腰作出高,延长两腰也是关键;记着平移对角线,上下底和差就出现;如果出现腰中点,就把中位线细心连;上述方法不奏效,过中点旋转成全等;灵活添加辅助线,帮你度过梯形难关;想要易解梯形题,还得注意特题特解;注意梯形割与补,巧变成为□和△,基本图形如下:
一、平移对角线:平移一条对角线,使之经过梯形的另一个顶点. 1.如图,在等腰梯形ABCD 中,AB ∥CD,AC ⊥BD,梯形的高CF 为10, 求梯形ABCD 的面积。
2.已知,如图,等腰梯形ABCD 中,
,
,
,
于E ,求
的长。
二、平移一腰或两腰:平移一腰,使之经过梯形的另一个顶点或另条腰的中点;或者同时移动两腰
使它们交于一点。 3.如图,等腰梯形ABCD 两底之差等于一腰的长,那么这个梯形 较小的一个内角是( )
A.9O °
B.6O °
C.45°
D.30°
4.已知:如图,等腰梯形ABCD 中,
,
,
,
,求
的度数。
5.如图,在梯形ABCD 中,AD ∥BC .AD E D C B A H G F E D C B A F E D C A 三、延长两腰:将梯形两腰延长相交构造三角形。 6.在梯形ABCD 中,AD ∥BC ,∠ABC=∠BCD=60°,AD+BC=30,BD 平分∠ABC ,求梯形的周长。 7.已知:在四边形ABCD 中,有 , , 。求证:四边形ABCD 为等腰 梯形。 四、作梯形的高:过梯上底的两个端点分别作梯形的高。 8.已知等腰梯形的一个内角为60°,它的上底是3cm , 腰长是4cm ,则下底是 。 9.如图,在梯形ABCD 中,已知,,,,求梯 形ABCD 的面积。 五.连接梯形一顶点及一腰的中点。 10.在梯形ABCD 中,AD ∥BC, E 、F 分别为AB 、CD 的中点, 求证:EF=1/2 (AD+BC) E D C B A F E D C B A G F E D C B A 六.过一腰的中点作另一腰的平行线。 11.在梯形ABCD 中,AD ∥BC, E 为CD 的中点, 求证:S △ABE=1/2S 梯形ABCD 七.作中位线 12.在梯形ABCD 中,AB ∥CD,M 为AD 的中点,AB+CD=BC,求证:BM ⊥CM 13.已知,如图,在直角梯形ABCD 中,, ,M 位CD 的中点,求证: 。 N M E D C B A N M D C B A 例谈梯形中的常用辅助线 最重要;平移两腰作出高,延长两腰也是关键;记着平移对角线,上下底和差就出现;如果出现腰中点,就把中位线细心连;上述方法不奏效,过中点旋转成全等;灵活添加辅助线,帮你度过梯形难关;想要易解梯形题,还得注意特题特解;注意梯形割与补,巧变成为□和△.基本图形如下: 一、平移 1、平移一腰:从梯形的一个顶点作一腰的平行线,把梯形转化为一个三角形和一个平行四边形。[例1]如图,梯形ABCD的上底AD=3,下底BC=8 ,腰 CD=4,求另一腰AB的取值范围。 A B C D E 【变式1】已知:如图,在梯形ABCD中,.求证:. 【变式2】已知:如图,在梯形中, .求证:梯形是等腰梯形. 2、平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到同一个三角形中。 [例2]如图,在梯形ABCD中,AB//CD,∠D+∠C=90°,BC=1,AD=3,E、F分别是AB、CD的中点,连接EF,求EF的长。 【变式】如图,在梯形中,,,、为、的中点。求 证:EF=1 2 (CD-AB) 3、平移对角线:一般是过上底的一个端点作一条对角线的平行线,与另一底的延长线相交,得到一 个平行四边形和三角形,把梯形问题转化为平行四边形和三角形问题解决. 【例3】.如图,等腰梯形中, , ,且 ,是高,是中位线,求证:. 【变式1】在等腰梯形ABCD中,AD//BC,AD=3,BC=7,BD=2 5,求证:AC⊥BD。 【变式2】(平移对角线)已知梯形ABCD的面积是32,两底与高的和为16,如果其中一条对角线与两底垂直,则另一条对角线长为_____________ [例4]在梯形ABCD中,AD//BC,AC=15cm,BD=20cm,高DH=12cm,求梯形ABCD的面积。 二、延长:即延长两腰相交于一点,可使梯形转化为三角形。 [例5]在梯形ABCD中,AD//BC,∠B=50°,∠C=80°,AD=2,BC=5,求CD的长。 【变式1】.如图,在梯形中, , ,梯形的面积与梯形的面积相等.求证: . 【变式2】所示,四边形ABCD中,AD不平行于BC,AC=BD,AD=BC. 判断四边形ABCD的形状,并证明你的结论. 三、作对角线:即通过作对角线,使梯形转化为三角形。 [例6]在直角梯形ABCD中,AD//BC,AB⊥AD,BC=CD,BE⊥CD于点E,求证:AD=DE。 A B C D 等腰三角形常用辅助线专题练习 1.如图:已知,点D、E在三角形ABC的边BC上,AB=AC, AD二AE,求证:BD=CEo 证明:作AF_LBC,垂足为F,则AF±DEo VAB=AC, AD=AE 又VAF±BC , AF±DE, ABF=CF, DF=EF (等腰三角形底边上的高与底边上的中线互相重合)。..?BD=CE. 2.如图,在三角形ABC中,AB二AC,AF平行BC于F, D是AC边上任意一点,延RBA到E,使AE=AD,连接DE,试判断直线AF与DE的位置关系,并说明理由 解:AF1DE.理由:延长ED 交BC 于G, VAB=AC, AE=AD /. ZB=ZC, ZE=ZADE A ZB+ZE=ZC+ZADE V ZADE=ZCDG A ZB+ZE=ZC+Z CDG VZB+ZE=ZDGC, ZC+ZCDG=ZBGE, ZBGE+ZCGD=180° AZ BGE=ZCGD=90° AEG±BC. VAF/7BC AAF±DE. E 解法2: 过A 点作AABC 底边上的高, BC 证明 AF±DE 3. 如图, A ABC 中,BA=BC,点D 是A B 延长线上一点,DF±A C 交BC 于 E,求证: A DBE 是等腰三角形。 证明:在AABC 中, VBA=BC, A ZA=ZC, VDF1AC, A ZC+Z FEC=90° , ZA+ZD=90° , :. ZFEC^ZD V ZFEC^ZBED, ZBED= 4.如图,AABC中,AB二AC, E在AC ±,且AD=AE, DE的延长线与BC相交于F。求证:DF_LBC. 证明:VAB=AC, AZB=ZC, 又VAD=AE, A ZD=ZAED, 若把“AD=AE”与结论“DF_LBC”互换,结论也成立。 若把条件"AB=AC”与结论“DF_LBC”互换,结论依然成立。 证明:连接AC, AD 梯形中添加辅助线的六种常用技巧 浙江唐伟锋 梯形是不同于平行四边形的一类特殊四边形, 解决梯形问题的基本思路是通过添加辅助 线,将梯形进行割补、拼接转化为三角形、平行四边形问题进行解决。一般而言,梯形中添 加辅助线的常用技巧主要有以下几种—— 一、平移一腰 从梯形的一个顶点作一腰的平行线, 将梯形转化为平行四边形和三角形, 从而利用平行 四边形的性质,将分散的条件集中到三角形中去,使问题顺利得解。 例1、如图①,梯形 ABCD 中AD // BC , AD=2cm , BC=7cm , AB=4cm ,求CD 的取值范围。 解:过点D 作DE // AB 交BC 于E , ?/ AD // BC , DE // AB ???四边形ABED 是平行四边形(两组对边分别平行的四边形是平行四边形) /? DE=AB=4cm , BE=AD=2cm ? EC=BC — BE=7 — 2=5cm 在厶DEC 中,EC — DE v CD v EC + DE (三角形两边之和大于第三边,两边之差小于 第三边) ? 1cm v CD v 9cm 。 、延长两腰 将梯形的两腰延长,使之交于一点,把梯形转化为大、小两个 三角形,从而利用特殊三角形的有关性质解决梯形问题。 例2、如图②,已知梯形 ABCD 中,AD // BC , / B= / C ,求证: 图② 梯形ABCD 是等腰梯形。 图① E 证明:延长BA 、CD ,使它们交于 E 点, ?/ AD // BC ???/ EAD= / B ,/ EDA= / C (两直线平行,同位角相等) 又??? B= / C ???/ EAD= / EDA ? EA=ED , EB=EC (等角对等边) ? AB=DC ?梯形ABCD 是等腰梯形(两腰相等的梯形是等腰梯形) 三、平移对角线 从梯形上底的一个顶点向梯形外作一对角线的平行线, 与下底延长线相交构成平行四边 形和一特殊三角形(直角三角形、等腰三角形等) 。 例3、如图③,已知梯形 ABCD 中,AD=1. 5cm, BC=3.5cm,对角线 AC 丄BD ,且BD=3cm , AC=4cm ,求梯形 ABCD 的面积。 解:过点D 作DE // AC 交BC 延长线于E ?/ AD // BC , DE // AC ?四边形 ACED 是平行四边形(两组对边分别平行的四 边形是平行四边形) ? CE=AD=1 . 5cm, DE=AC=4cm ???AC 丄 BD ? DE 丄 BD BC ) h 2(CE BC ) h -BE h (h 为梯形的高) 1 1 6cm 2 BD DE 3 4 2 2 四、作高线 梯形 ABCD = -(AD 2 几何最难的地方就是辅助线的添加了,但是对于添加辅助线,还是有规律可循的,下面可小编给大家整理了一些常见的添加辅助线的方法,掌握了对你一定有帮助! 1 三角形中常见辅助线的添加 1. 与角平分线有关的?? (1)可向两边作垂线。?? (2)可作平行线,构造等腰三角形?? (3)在角的两边截取相等的线段,构造全等三角形?? 2. 与线段长度相关的?? (1)截长:证明某两条线段的和或差等于第三条线段时,经常在较长的线段上截取一段,使得它和其中的一条相等,再利用全等或相似证明余下的等于另一条线段即可?? (2)补短:证明某两条线段的和或差等于第三条线段时,也可以在较短的线段上延长一段,使得延长的部分等于另外一条较短的线段,再利用全等或相似证明延长后的线段等于那一条长线段即可?? (3)倍长中线:题目中如果出现了三角形的中线,方法是将中线延长一倍,再将端点连结,便可得到全等三角形。?? (4)遇到中点,考虑中位线或等腰等边中的三线合一。? 3. 与等腰等边三角形相关的?? (1)考虑三线合一?? (2)旋转一定的度数,构造全都三角形,等腰一般旋转顶角的度数,等边旋转60?° 2 四边形中常见辅助线的添加 特殊四边形主要包括平行四边形、矩形、菱形、正方形和梯形.在解决一些和四边形有关的问题时往往需要添加辅助线。下面介绍一些辅助线的添加方法。 1. 和平行四边形有关的辅助线作法? ???? 平行四边形是最常见的特殊四边形之一,它有许多可以利用性质,为了利用这些性质往往需要添加辅助线构造平行四边形。? (1)利用一组对边平行且相等构造平行四边形? (2)利用两组对边平行构造平行四边形? (3)利用对角线互相平分构造平行四边形?? 2. 与矩形有辅助线作法? ? (1)计算型题,一般通过作辅助线构造直角三角形借助勾股定理解决问题? (2)证明或探索题,一般连结矩形的对角线借助对角线相等这一性质解决问题.和矩形有关的试题的辅助线的作法较少. 3. 和菱形有关的辅助线的作法? ??? ? ? 四边形常用的辅助线做法 作辅助线的方法 一:中点、中位线,延线,平行线。 如遇条件中有中点,中线、中位线等,那么过中点,延长中线或中位线作辅助线,使延长的某一段等于中线或中位线;另一种辅助线是过中点作已知边或线段的平行线,以达到应用某个定理或造成全等的目的。 二:垂线、分角线,翻转全等连。 如遇条件中,有垂线或角的平分线,可以把图形按轴对称的方法,并借助其他条件,而旋转180度,得到全等形,,这时辅助线的做法就会应运而生。其对称轴往往是垂线或角的平分线。 三:边边若相等,旋转做实验。 如遇条件中有多边形的两边相等或两角相等,有时边角互相配合,然后把图形旋转一定的角度,就可以得到全等形,这时辅助线的做法仍会应运而生。其对称中心,因题而异,有时没有中心。故可分“有心”和“无心”旋转两种。 四:造角、平、相似,和、差、积、商见。 如遇条件中有多边形的两边相等或两角相等,欲证线段或角的和差积商,往往与相似形有关。在制造两个三角形相似时,一般地,有两种方法:第一,造一个辅助角等于已知角;第二,是把三角形中的某一线段进行平移。故作歌诀:“造角、平、相似,和差积商见。” 五:面积找底高,多边变三边。 如遇求面积,(在条件和结论中出现线段的平方、乘积,仍可视为求面积),往往作底或高为辅助线,而两三角形的等底或等高是思考的关键。 如遇多边形,想法割补成三角形;反之,亦成立。 四边形 平行四边形出现,对称中心等分点。梯形问题巧转换,变为△和□。 平移腰,移对角,两腰延长作出高。如果出现腰中点,细心连上中位线。 上述方法不奏效,过腰中点全等造。证相似,比线段,添线平行成习惯。 等积式子比例换,寻找线段很关键。直接证明有困难,等量代换少麻烦。 斜边上面作高线,比例中项一大片。 添加辅助线解特殊四边形题 特殊四边形主要包括平行四边形、矩形、菱形、正方形和梯形.在解决一些和四边形有关的问题时往往需要添加辅助线.下面介绍一些辅助线的添加方法. 和平行四边形有关的辅助线作法 平行四边形是最常见的特殊四边形之一,它有许多可以利用性质,为了利用这些性质往往需要添加辅助线构造平行四边形. 平行四边形中常用辅助线的添法 平行四边形(包括矩形、正方形、菱形)的两组对边、对角和对角线都具有某些相同性质,所以在添辅助线方法上也有共同之处,目的都是造就线段的平行、垂直,构成三角形的全等、相似,把平行四边形问题转化成常见的三角形、正方形等问题处理,其常用方法有下列几种,举例简解如下: (1)连对角线或平移对角线: (2)过顶点作对边的垂线构造直角三角形 (3)连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线 (4)连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形。 (5)过顶点作对角线的垂线,构成线段平行或三角形全等. 等腰三角形常用辅助线专题练习 (含答案) 1.如图:已知,点D、E在三角形ABCの边BC上, AB=AC,AD=AE,求证:BD=CE。 证明:作AF⊥BC,垂足为F,则AF⊥DE。∵AB=AC,AD=AE 又∵AF⊥BC ,AF⊥DE,∴BF=CF,DF=EF (等腰三角形底边上の高与底边上の中线互相重合)。∴BD=CE. 2.如图,在三角形ABC中,AB=AC,AF平行BC于F, D是AC边上任意一点,延长BA到E,使AE=AD,连接 DE,试判断直线AF与DEの位置关系,并说明理由 解:AF⊥DE.理由:延长ED交BC于G,∵AB=AC,AE=AD ∴∠B=∠C,∠E=∠ADE ∴∠B+∠E=∠C+∠ADE ∵∠ADE=∠CDG ∴∠B+∠E=∠C+∠CDG ∵∠B+∠E=∠DGC,∠C+∠CDG=∠BGE,∠BGE+∠CGD=180°∴∠BGE=∠CGD=90°∴EG⊥BC.∵AF∥BC ∴AF⊥DE. 解法2: 过A点作△ABC底边上の高, 再用∠BAC=∠D+AED=∠2∠ADE, 即∠CAG=∠AED,证明AG∥DE 利用AF∥BC证明AF⊥DE 3.如图,△ABC中,BA=BC,点D是AB延长线上一点, DF⊥AC交BC于E,求证:△DBE是等腰三角形。 证明:在△ABC中,∵BA=BC,∴∠A=∠C,∵DF⊥AC,∴∠C+∠FEC=90°,∠A+∠D=90°,∴∠FEC=∠D ∵∠FEC=∠BED,∴∠BED= ∠D,∴BD=BE,即△DBE是等腰三角形. 4. 如图,△ABC中,AB=AC,E在AC上,且AD=AE,DE の延长线与BC相交于F。求证:DF⊥BC. 证明:∵AB=AC,∴∠B=∠C,又∵AD=AE,∴∠D=∠AED, ∴∠B+∠D=∠C+∠AED,∴∠B+∠D=∠C+∠CEF, ∴∠EFC=∠BFE=180°× 1/2 = 90°,∴DF⊥BC; 若把“AD =AE”与结论“DF⊥BC”互换,结论也成立。 若把条件“AB=AC”与结论“DF⊥BC”互换,结论依然成立。 5. 如图,AB=AE,BC=ED, ∠B=∠E,AM⊥CD, A 求证:CM=MD. 证明:连接AC,AD ∵AB=AE,∠B=∠E,BC=ED ∴△ABC≌△AED(SAS) 第3课时《四边形》(3) ——梯形及梯形中常用的辅助线的作法 【知识点拨】 一、梯形的定义: 一组对边平行,另一组对边不平行的四边形叫做梯形。 直角梯形的定义:有一个角是直角的梯形 等腰梯形的定义:两腰相等的梯形。 等腰梯形的性质:等腰梯形同一底边上的两个角相等;等腰梯形的两条对角线相等。 等腰梯形判定定理:(1)同一底上两个角相等的梯形是等腰梯形。 (2)对角线相等的梯形是等腰梯形。 [例题1]1、下列命题中,正确的个数是( ) ①如果一个梯形是轴对称图形,则它一定是等腰梯形②有两个角相等的梯形,一定是等腰梯形③一组对边平行,另一组对边相等的四边形事实上是等腰梯形④对角线相等的梯形是等腰梯形 A .1个 B .2个 C .3个 D .4个 【答案】:B 2、已知梯形的两个对角分别是78和120,则另两个角分别为( ) A .78和120 B .102和 60 C .120和 78 D .60和120 【答案】:B 3、如图所示,在四边形ABCD 中,AD BC E ∥,是AB 的中点, 若DEC △的面积为S ,则四边形ABCD 的面积为( ) A .5 2S B .2S C .74 S D . 9 4 S 【答案】:B 4、已知,如图所示,在等腰梯形ABCD 中,.AD BC PA PD =∥,求证:PB PC =. 【答案】:证明:四边形ABCD 是等腰梯形. .B A D C D A ∴∠ =∠ 又PA PD =, 1 2. .B A P C D P ∴∠=∠∴∠=∠ 在PBA △和PCD △中, A B D C B A P C D P P A =∠=∠=, ,. .. P B A P C D P B P C ∴∴=△≌△ 1 2 A D C P B A E B C D 第3题图 【MeiWei_81重点借鉴文档】 有等腰三角形时常用的辅助线⑴作顶角的平分线,底边中线,底边高线 例:已知,如图,AB = AC, BDLAC于D, 求证:/ BAC = 2/DBC 证明:(方法一)作Z BAC的平分线AE,交BC于E,则Z 1 = Z 2 = 又v AB = AC 1 -Z BAC 2 ??? AEL BC ???/ 2+Z ACB = 90° ??? BD L AC ???/ DBCM ACB = 90° ???/ 2 = / DBC ???/ BAC = 2 / DBC (方法二)过A作AEL BC于E (过程略) (方法三)取BC中点E,连结AE (过程略) ⑵有底边中点时,常作底边中线 例:已知,如图,△ ABC中, AB = AC,D 为BC 中点,DEL AB 于E,DFL AC于F, 求证:DE = DF 证明:连结AD. v D为BC中点, ??? BD = CD 又v AB =AC ??? AD平分/ BAC v DEL AB, DFL AC ??? DE = DF ⑶将腰延长一倍,构造直角三角形解题 例:已知,如图,△ ABC中, AB = AC在BA延长线和AC上各取一点E、F,使AE = AF, 求证:EFL BC 证明:延长BE至U N,使AN = AB,连结CNJ则AB = AN = AC ???/ B = / ACB, / ACN = / ANC vZ B+Z ACB^Z ACNbZ ANC = 180° ??? 2Z BC外2Z ACN = 180° ???Z BCAbZ ACN = 90° 即Z BCN = 90° ?NCL BC v AE = AF ?Z AEF = Z AFE 又vZ BAC = Z AEF + Z AFE Z BAC = Z ACN + Z ANC ?Z BAC =2Z AEF = 2 Z ANC ?Z AEF = Z ANC ?EF// NC ?EFL BC 初中几何常见辅助线做法 一、三角形常见辅助线做法 方法1:有关三角形中线的题目,常将中线加倍; 含有中点的题目,常常做三角形的中位线,把结论恰当的转移 例1、如图5-1:AD 为△ABC 的中线,求证:AB +AC >2AD 。 【分析】:要证AB +AC >2AD ,由图想到: AB +BD >AD,AC +CD >AD ,所以有AB +AC + BD +CD >AD +AD =2AD ,左边比要证结论多BD +CD ,故不能直接证出此题,而由2AD 想到 要构造2AD ,即加倍中线,把所要证的线段转移到同一个三角形中去。 证明:延长AD 至E ,使DE=AD ,连接BE ,则AE =2AD ∵AD 为△ABC 的中线 (已知) ∴BD =CD (中线定义) 在△ACD 和△EBD 中 ?? ???=∠=∠=)()()(辅助线的作法对顶角相等已证ED AD EDB ADC CD BD ∴△ACD ≌△EBD (SAS ) ∴BE =CA (全等三角形对应边相等) ∵在△ABE 中有:AB +BE >AE (三角形两边之和大于第三边) ∴AB +AC >2AD 。 例2、如图4-1:AD 为△ABC 的中线,且∠1=∠2,∠3=∠4,求证:BE +CF >EF 证明:延长ED 至M ,使DM=DE ,连接 CM ,MF 。在△BDE 和△CDM 中, ∵?? ???=∠=∠=)()(1)(辅助线的作法对顶角相等中点的定义MD ED CDM CD BD ∴△BDE ≌△CDM (SAS ) 又∵∠1=∠2,∠3=∠4 (已知) ∠1+∠2+∠3+∠4=180°(平角的定义) ∴∠3+∠2=90°,即:∠EDF =90° 1 4-图A B C D E F M 123 4A B C D E 1 5-图 专题讲义 平行四边形+几何辅助线的作法 一、知识点 1.四边形的内角和与外角和定理: (1)四边形的内角和等于360°; (2)四边形的外角和等于360°. 2.多边形的内角和与外角和定理: (1)n 边形的内角和等于(n-2)180°; (2)任意多边形的外角和等于360°. 3.平行四边形的性质: 四边形ABCD 是平行四边形 ?????????. 54321)邻角互补()对角线互相平分;()两组对角分别相等; ()两组对边分别相等;()两组对边分别平行;( 4、平行四边形判定方法的选择 5、和平行四边形有关的辅助线作法 (1)利用一组对边平行且相等构造平行四边形 例1、如图,已知点O 是平行四边形ABCD 的对角线AC 的中点,四边形OCDE 是平行四边形 求证: OE 与AD 互相平分. (2)利用两组对边平行构造平行四边形 例2、如图,在△ABC 中,E 、F 为AB 上两点,AE=BF ,ED//AC ,FG//AC 交BC 分别为D ,G. 求证: ED+FG=AC. (3)利用对角线互相平分构造平行四边形 例3、如图,已知AD 是△ABC 的中线,BE 交AC 于E ,交AD 于F ,且AE=EF.求证BF=AC. A B C D 1234A B C D A B D O C 性质 判定 说明:当已知条件中涉及到平行,且要求证的结论中和平行四边形的性质有关,可说明:当图形中涉及到一组对边平 行时,可通过作平行线构造另一组说明:本题通过利用对角线互相平分构造平行 四边形,实际上是采用了平移法构造平行四边 形.当已知中点或中线应思考这种方法. (4)连结对角线,把平行四边形转化成两个全等三角形。 例4、如图,在平行四边形ABCD 中,点F E ,在对角线AC 上,且CF AE =,请你以F 为一个端点, 和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一条线段即可) (5)平移对角线,把平行四边形转化为梯形。 例5、如右图2,在平行四边形ABCD 中,对角线AC 和BD 相交于点O ,如果12=AC , 10=BD ,m AB =,那么m 的取值范围是( ) A 、111< 梯形的所有基础知识 首先认识一下梯形 定义:一组对边平行而对边不平行的四边形叫做梯形。 组成:在梯形ABCD中,平行的两边AB与CD叫做梯形的底,不平行的两边AD与BC叫做梯形的腰。夹在两底之间`与底垂直的线段叫做梯形的高。 分类:1 两腰相等的梯形(P28页图1 - 34)叫做等腰梯形 2 一腰与底垂直的梯形(P28页图 1- 35)叫做直角梯形 好的,以上是梯形的基本知识,下面就是深入的了解梯形了 梯形的性质定理 性质定理一:等腰梯形同一底上的两个内角相等(课本P29) 性质定理二:等腰梯形的两条对角线相等(课本P29) 然后有一个特殊一点儿的梯形就是“等腰梯形” 等腰梯形的判定定理:同一底上的两个内角相等的梯形是等腰梯形。 (P30页的交流与发现小胖孩儿和小姑娘的话要仔细看看, 还有就是P31的例2重点看看。) 重点来咯~ ~ ~ 接下来就是今天的主角登场了 ~ 它就是“等腰梯形的辅助线” 顾名思义,“等腰梯形的辅助线”就是添加一条等腰梯形上本没有的线段来帮助我们很好的解决这道题目(注意!前提是这个图形必须是等腰梯形) 但该怎么添加才会让我们做起题目来更简单更直接呢 针对梯形的学习这就需要掌握一些添加辅助线的方法了 好的长话短说下面就是四种添加辅助线的方法。 第一种方法: P28页下半部分的例题就是第一种添加辅助线解梯形的方法 这种辅助线叫做“平移一腰” 它的做法是“过点D作DE∥AB,交于BC于点E”(课本P28 图1-36) DE就是第一种辅助线。 第二种方法: 叫做“作高” 它的做法是:过点A作AF⊥于BC 垂足为 F 过点D作DE⊥于BC 垂足为 E AF与DE 就是第二种辅助线。 第三种方法: 等腰三角形常用辅助线 专题练习 (含答案) AB=AC,AF 平行BC 于F , D 是AC 边上任意一点,延 长 BA AF 与DE 的位置关系,并说 明理由 ?/ AB=AC , AE=AD B= / C , / E= / ADE ???/ B+ / E= / C+ / CDG ?// B+ / E= / DGC , ???/ BGE= / CGD=90 ?? EG 丄 BC . ?/ AF // BC 解法2: 过A 点作△ ABC 底边上的高, 再用/ BAC= / D+AED= / 2/ ADE,即/ CAG= / AED,证明 AG // DE 利用 AF // BC 证明 AF 丄 DE 3.如图,△ ABC 中,BA=BC ,点D 是AB 延长线上一点, DF 丄AC 交BC 于E,求证:△ DBE 是等腰三角形。 证明:在 △ ABC 中,?/ BA=BC , ???/A= / C , ?/ DF 丄 AC , / A+ / D=90 , ???/ FEC= / D v/ FEC= / BED , BED= / D , 是等腰三角形. 4.如图,△ ABC 中,AB=AC,E 在AC 上,且 AD=AE,DE 的延长线与 DF 丄 BC. 证明:v AB=AC , ???/ B= / C , 又 v AD=AE , ??/ D= / AED , ???/ B+ / D= / C+ / AED , ???/ B+ / D= / C+/ CEF , ???/ EFC= / BFE=180 X 1/2 = 90 , ? DF 丄 BC; 若把“AD =Ae 与结论“DFL BC ”互换,结论也成立。 若把条件“AB=AC 与结论“ DFL BC ”互换,结论依然成立。 5. 如图,AB=AE,BC=ED, / B= / E,AM 丄 CD, A 求证:CM=MD. 证明:连接AC,AD ?/ AB=AE, / B= / E,BC=ED ??△ ABC ◎△ AED(SAS) 1.如图:已知,点 D 、E 在三角形 ABC 的边BC 上, 证 明:作AF 丄BC ,垂足为 又??? AF 丄 BC , AF 丄 DE , 互相重合)。 ??? BD=CE. AB=AC , AD=AE ,求证: F ,贝U AF 丄 DE 。 ?/ AB=AC , AD=AE ??? BF=CF , DF=EF (等腰三角形底边上的高与 BD=CE 。 底边上的中线 2.如图,在三角形 ABC 中, 到E ,使AE=AD , 连接DE ,试判断直线 解:AF 丄DE .理由:延长ED 交BC 于G , ???/ B+ / E= / C+/ ADE ?// ADE= / CDG / C+ / CDG= / BGE , / BGE+ / CGD=18° ??? AF 丄 DE . ???/ C+ / FEC=90 , BC 相交于F 。求证: 梯形中添加辅助线的六种常 用技巧 -标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII 梯形中添加辅助线的六种常用技巧 浙江唐伟锋 梯形是不同于平行四边形的一类特殊四边形,解决梯形问题的基本思路是通过添加辅助线,将梯形进行割补、拼接转化为三角形、平行四边形问题进行解决。一般而言,梯形中添加辅助线的常用技巧主要有以下几种—— 一、平移一腰 从梯形的一个顶点作一腰的平行线,将梯形转化为平行四边形和三角形,从而利用平行四边形的性质,将分散的条件集中到三角形中去,使问题顺利得解。 例1、如图①,梯形ABCD中AD∥BC,AD=2cm ,BC=7cm,AB=4cm,求CD的取值范围。 解:过点D作DE∥AB交BC于E, ∵AD∥BC,DE∥AB ∴四边形ABED是平行四边形(两组对边分别平行的四边形是平行四边形) ∴DE=AB=4cm,BE=AD=2cm ∴EC=BC-BE=7-2=5cm 在△DEC中,EC-DE<CD<EC+DE(三角形两边之和大于第三边,两边之差小于第三边) ∴1cm<CD<9cm。 二、延长两腰 将梯形的两腰延长,使之交于一点,把梯形转化为 大、小两个三角形,从而利用特殊三角形的有关性质解决 梯形问题。 例2、如图②,已知梯形ABCD中,AD∥BC,∠B=∠ C ,求证:梯形ABC D 是等腰梯形。 证明:延长BA 、CD ,使它们交于E 点, ∵AD ∥BC ∴∠EAD=∠B ,∠EDA=∠C (两直线平行,同位角相等) 又∵B=∠C ∴∠EAD=∠EDA ∴EA=ED ,EB=EC (等角对等边) ∴AB=DC ∴梯形ABCD 是等腰梯形(两腰相等的梯形是等腰梯形)。 三、平移对角线 从梯形上底的一个顶点向梯形外作一对角线的平行线,与下底延长线相交构成平行四边形和一特殊三角形(直角三角形、等腰三角形等)。 例3、如图③,已知梯形ABCD 中,AD=,BC=,对角线AC ⊥BD ,且BD=3cm ,AC=4cm ,求梯形ABCD 的面积。 解:过点D 作DE ∥AC 交BC 延长线于E ∵AD ∥BC ,DE ∥AC ∴四边形ACED 是平行四边形(两组对边分别平 行的四边形是平行四边形) ∴CE=AD=,DE=AC=4cm ∵AC ⊥BD ∴DE ⊥BD ∴S 梯形ABCD =111()()222 AD BC h CE BC h BE h +?=+?=?(h 为梯形的高) 211346cm 22 BD DE =?=??= 。 19.3 等腰梯形的判定 教学目标: 1.掌握等腰梯形的三种判定方法。 2.能够运用等腰梯形的判定方法进行简单的证明。 3.通过添加辅助线,把梯形问题转化成平行四边形或三角形问题,体会图形变换的 方法和转化思想。 教学重点:探究等腰梯形的判定定理. 教学难点:灵活地运用等腰梯形的常规辅助线,并借助等腰梯形的判定解决问题。 教学过程: 一.复习巩固 (1)上节课所学习的梯形的常用辅助线 (2) 等腰梯形的性质: 1、等腰梯形的 相等 2、等腰梯形在同一底上的 相等 3、等腰梯形的两条 相等 (3) 写出等腰梯形的性质对应的三个逆命题: 1、 。 2、 。 3、 。 二.小组探究 证明 (1)逆命题二:在同一底上的两个角相等的梯形是等腰梯形(用三种方法) 已知在梯形ABCD 中,AD ∥BC ,∠B=∠C , 等腰梯形的判定定理二: 梯形为等腰梯形 (2)逆命题三:对角线相等的梯形是等腰梯形。 已知:如图,在梯形ABCD 中,AD ∥BC ,AC=BD 。 求证:四边形ABCD 是等腰梯形。 等腰梯形的判定定理三: 的梯形是等腰梯形 知识梳理 等腰梯形的三种性质与判定(二人小组互查) 三.自我检测 判断正误 (1)有两个角相等的梯形一定是等腰梯形. ( ) (2)两条对角线相等的梯形一定是等腰梯形. ( ) (3)如果一个梯形是轴对称图形,则它一定是等腰梯形. (4)一组对边平行,另一组对边相等的四边形一定是等腰梯形. ( ) (5)对角互补的梯形一定是等腰梯形. ( ) 四.巩固提高 已知:在梯形ABCD中,AD//BC,∠ACB=∠DBC. 五.拓展延伸(课后思考) 如图,等腰梯形ABCD中,AD∥BC, AC⊥BD,AD+BC=10,DE⊥BC于E, 六.领会与感悟 等腰三角形中做辅助线的八种常用方法几何图形中添加辅助线,往往能把分散的条件集中,使隐蔽的条件显露,将复杂的问题简单化.例如:作“三线”中的一线或平行线证线段相等,利用截长补短证线段和差关系或求角的度数,利用加倍折半法证线段的倍分关系等,将不在同一个三角形的线段转移到同一个三角形(或两个全等三角形)中,然后运用等腰(或全等三角形)的性质来解决问题. 方法1 等腰三角形中有底边上的中点时常作底边上的中线 1.如图,在三角形ABC中,∠A=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF,求证:(1)DE=DF.(2)DE⊥DF 方法2 等腰三角形中没有底边上的中点时常作底边上的高 2.如图,△ABC中,AC=2AB,AD平分∠BAC交BC于D,E是AD上一点,且EA=EC,求证:EB⊥AB. 方法3 等腰三角形中证与腰有关联的线段时常作腰的平行线或垂线 3.如图,在△ABC中,AB=AC ,点P从点B出发沿线段BA移动(点P与A,B 不重合),同时,点Q从点C出发沿线段AC的延长线移动,点P,Q移动的速度相同,PQ与直线BC相交于点D. (1)试说明:PD=QD (2)过点P作直线BC的垂线,垂足为E,P,Q在移动的过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由. 方法4 等腰三角形证与底有关的线段时常作底的平行线 4.如图,等边三角形ABC中,D是边AC延长线上一点,延长BC至E,使CE=AD, DG⊥BE于G,求证:BG=EG. 方法5补形法构造等腰三角形 5.如图,AB∥CD,∠1=∠2,AD=AB+CD,求证:(1)BE=CE;(2)AE⊥DE;(3)AE平分∠BAD. 方法6 倍长中线法构造等腰三角形 6.如图,△ABC中,AD为中线,点E为AB上一点,AD,CE交于点F,且CE=EF,求证:AB=CF 八年级数学培优训练题 补形法的应用 班级_________ 姓名_______________________________ 分数_______________________ 一些几何题的证明或求解,由原图形分析探究,有时显得十分繁难,若通过适当的“补形”来进行,即添置适当的辅助线,将原图形填补成一个完整的、特殊的、简单的新图形,则能使原问题的本质得到充分的显示,通过对新图形的分析,使原问题顺利获解。这种方法,我们称之为补形法,它能培养思维能力和解题技巧。我们学过的三角形、特殊四边形、圆等都可以作为“补形”的对象。现就常见的添补的图形举例如下,以供参考。 一、补成三角形 1. 补成三角形 例1.如图1,已知E为梯形ABCD勺腰CD的中点; 证明:△ ABE的面积等于梯形ABCD面积的一半。 分析:过一顶点和一腰中点作直线,交底的延长线于一点,构造等面积的三角形。这也是梯形中常用的辅助线添法之一。 略证: 2. 补成等腰三角形 例2 如图2.已知/ A= 90°,AB= AC, / 1 = / 2, CEL BD 求证:BD= 2CE 分析:因为角是轴对称图形,角平分线是对称轴,故根据对称 性作出辅助线,不难发现CF= 2CE,再证BD= CF即可。 略证: 3. 补成直角三角形 例3.如图3,在梯形ABCD中, AD// BC, / B+Z C= 90° F、G分别是AD BC的中点,若BC= 18, AD= 8,求FG的长 分析:从Z B、Z C互余,考虑将它们变为直角三角形的角, 故延长BA、CD要求FG 需求PF、PG 略解: 4. 补成等边三角形 例4.图4,A ABC是等边三角形,延长BC至D,延长BA至E,使AE= BD 连结CE ED 证明:EC= ED 分析:要证明EC= ED,通常要证Z ECD=Z EDC但难以实现。这样可采用补形法即延长BD到F,使BF= BE,连结EF。 略证: 梯形常见辅助线作法 1 1、平移法 2 (1)梯形内平移一腰(过一顶点做腰的平行线) 3 [例1]如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠C=60°,AD=15cm, 4 BC=49cm,求CD的长. 5 解:过D作DE∥AB交BC于E,则四边形ABED为平行四边形. 6 ∴AD=BE=15cm,AB=DE. 7 ∴EC=BC-BE=BC-AD=49-15=34cm. 8 又∵AB=CD,∴ DE=CD. 9 又∵∠C=60°, 10 ∴△CDE是等边三角形, 11 即CD=EC=34cm. 12 (2)梯形外平移一腰(过一顶点做腰的平行线) 13 [例2]如图,在梯形ABCD中,AB∥CD,四边形ACED是平行四边形,延长DC交BE于F. 求14 证:EF=FB 15 证明:过点B作BG∥AD,交DC的延长线于G 16 ∴四边形ABGD是平行四边形∴AD=BG 17 ∵ACED中,AD∥CE AD=CE 18 ∴CE∥BG且CE=BG ∴∠CEF=∠GBF 19 又∵∠CFE=∠GFB 20 ∴△ECF≌△BGF( ASA) 21 ∴EF=FB 22 A D C E F B 点评:过梯形上底或下底的一个端点作另一腰的平行线,可将梯形转化为一个平行四边形23 和三角形。 24 (3)梯形内平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到25 同一个三角形中。 26 [例3]如图,已知:梯形ABCD中,AD∥BC, 27 ∠C+∠B=90°,M,N分别是AD,BC的中点. 28 求证:MN=1 () 2 BC AD 29 证明:过点E分别作AB、CD的平行线,交BC于点G、H , 30 则四边形ABGE,EDCH为平行四边形∴AE=BG,ED=HC 31 ∵AB∥EG ∴∠B=∠EGF 32 又∵DC∥EH ∴∠C=∠EHF 33 则∠EGH+∠EHG=∠B+∠C=90°,△EGH是直角三角形 34 ∵E、F分别是AD、BC的中点∴AE=ED,BF=CF ∴GF=FH 35 则有EF=1 2 GH= 1 2 (BC-BG-HC)= 1 2 (BC-AD) 36 (4)平移对角线(过一顶点做对角线的平行线)37 [例4]求证:对角线相等的梯形是等腰梯形 38 已知:在梯形ABCD中,AD∥BC,对角线 39 求证:AB=DC 40 证明:过点D作DE∥AC交BC的延长线于点E 41 B B 梯形辅助线专题训练 口诀:梯形问题巧转换,变为△和□。平移腰,移对角,两腰延长作出高。如果出现腰中点,细心连上中位线。上述方法不奏效,过腰中点全等造。 通常情况下,通过做辅助线,把梯形转化为三角形、平行四边形,是解梯形问题的基本思路。至于选取哪种方法,要结合题目图形和已知条件。常见的几种辅助线的作法如下: 作法 图形 平移腰,转化为三角形、平行四边形。 A B C D E 平移对角线。转化为三角形、平行四边形。 A B C D E 延长两腰,转化为三角形。 A B C D E 作高,转化为直角三角形和矩形。 A B C D E F 中位线与腰中点连线。 A B C D E F (一)、平移 1、平移一腰: 例1. 如图所示,在直角梯形ABCD 中,∠A =90°,AB ∥DC ,AD =15,AB =16,BC =17. 求CD 的长. 解:过点D 作DE ∥BC 交AB 于点E. 又AB ∥CD ,所以四边形BCDE 是平行四边形. 所以DE =BC =17,CD =BE. 在R t △DAE 中,由勾股定理,得 AE 2=DE 2-AD 2,即AE 2=172-152=64. 所以AE =8. 所以BE =AB -AE =16-8=8. 即CD =8. 例2如图,梯形ABCD 的上底AB=3,下底CD=8,腰AD=4,求另一腰BC 的取值范围。 解:过点B 作BM//AD 交CD 于点M , 在△BCM 中,BM=AD=4, CM=CD -DM=CD -AB=8-3=5, 所以BC 的取值范围是: 5-4 此文档下载后即可编辑 初中几何辅助线做法 辅助线,如何添?把握定理和概念。还要刻苦加钻研,找出规律凭经验。 三角形 图中有角平分线,可向两边作垂线。也可将图对折看,对称以后关系现。 角平分线平行线,等腰三角形来添。角平分线加垂线,三线合一试试看。 线段垂直平分线,常向两端把线连。要证线段倍与半,延长缩短可试验。 三角形中两中点,连接则成中位线。三角形中有中线,延长中线等中线。 四边形 平行四边形出现,对称中心等分点。梯形里面作高线,平移一腰试试看。 平行移动对角线,补成三角形常见。证相似,比线段,添线平行成习惯。 等积式子比例换,寻找线段很关键。直接证明有困难,等量代换少麻烦。 斜边上面作高线,比例中项一大片。 圆 半径与弦长计算,弦心距来中间站。圆上若有一切线,切点圆心半径连。 切线长度的计算,勾股定理最方便。要想证明是切线,半径垂线仔细辨。 是直径,成半圆,想成直角径连弦。弧有中点圆心连,垂径定理要记全。 圆周角边两条弦,直径和弦端点连。弦切角边切线弦,同弧对角等找完。 要想作个外接圆,各边作出中垂线。还要作个内接圆,内角平分线梦圆。 如果遇到相交圆,不要忘作公共弦。内外相切的两圆,经过切点公切线。 若是添上连心线,切点肯定在上面。要作等角添个圆,证明题目少困难。 辅助线,是虚线,画图注意勿改变。假如图形较分散,对称旋转去实验。 基本作图很关键,平时掌握要熟练。解题还要多心眼,经常总结方法显。 切勿盲目乱添线,方法灵活应多变。分析综合方法选,困难再多也会减。 一、见中点引中位线,见中线延长一倍 在几何题中,如果给出中点或中线,可以考虑过中点作中位线或把中线延长一倍来解决相关问题。 二、在比例线段证明中,常作平行线。 作平行线时往往是保留结论中的一个比,然后通过一个中间比与结论中的另一个比联系起来。 三、对于梯形问题,常用的添加辅助线的方法有 1、过上底的两端点向下底作垂线 2、过上底的一个端点作一腰的平行线 3、过上底的一个端点作一对角线的平行线 4、过一腰的中点作另一腰的平行线 5、过上底一端点和一腰中点的直线与下底的延长线相交 6、作梯形的中位线 7、延长两腰使之相交 四、在解决圆的问题中 1、两圆相交连公共弦。 2、两圆相切,过切点引公切线。 3、见直径想直角 4、遇切线问题,连结过切点的半径是常用辅助线 5、解决有关弦的问题时,常常作弦心距。梯形中的常用辅助线总结与对应练习题
等腰三角形常用辅助线专题练习含答案
梯形中添加辅助线的六种常用技巧
数学常见辅助线做法与小结
四边形辅助线常用做法
等腰三角形常用辅助线专题练习(含答案)汇总
第3课时:《平行四边形》(3)——梯形及梯形中常用的辅助线的作法
有等腰三角形时常用的辅助线
初中几何常用辅助线专题
专题二平行四边形常用辅助线的作法精排版
梯形部分-四种等腰梯形添加辅助线方法
等腰三角形常用辅助线专题练习(含答案)
梯形中添加辅助线的六种常用技巧
等腰梯形教学文档
等腰三角形中的常见辅助线
初二数学图形辅助线常见做法
最新梯形常见辅助线作法(教师版)
初二上梯形辅助线专题训练(非常经典)
初中平面几何常见添加辅助线的方法(完整资料).doc