
杨辉三角形规律
每行数字两边对称每行数字左右对称,由1开始逐渐变大,然后变小,回到1。
第n行的数字个数为n个。
第n行数字和为2^(n-1)。(2的(n-1)次方)
每个数字等于上一行的左右两个数字之和。可用此性质写出整个帕斯卡三角形。
将第2n+1行第1个数,跟第2n+2行第3个数、第2n+3行第5个数……连成一线,这些数的和是第2n个斐波那契数。将第2n行第2个数,跟第2n+1行第4个数、第2n+2行第6个数……这些数之和是第2n-1个斐波那契数。
第n行的第1个数为1,第二个数为1×(n-1),第三个数为1×(n-1)×(n-2)/2,第四个数为1×(n-1)×(n-2)/2×(n-3)/3…依此类推。
两个未知数和的n次方运算后的各项系数依次为杨辉三角的第(n+1)行
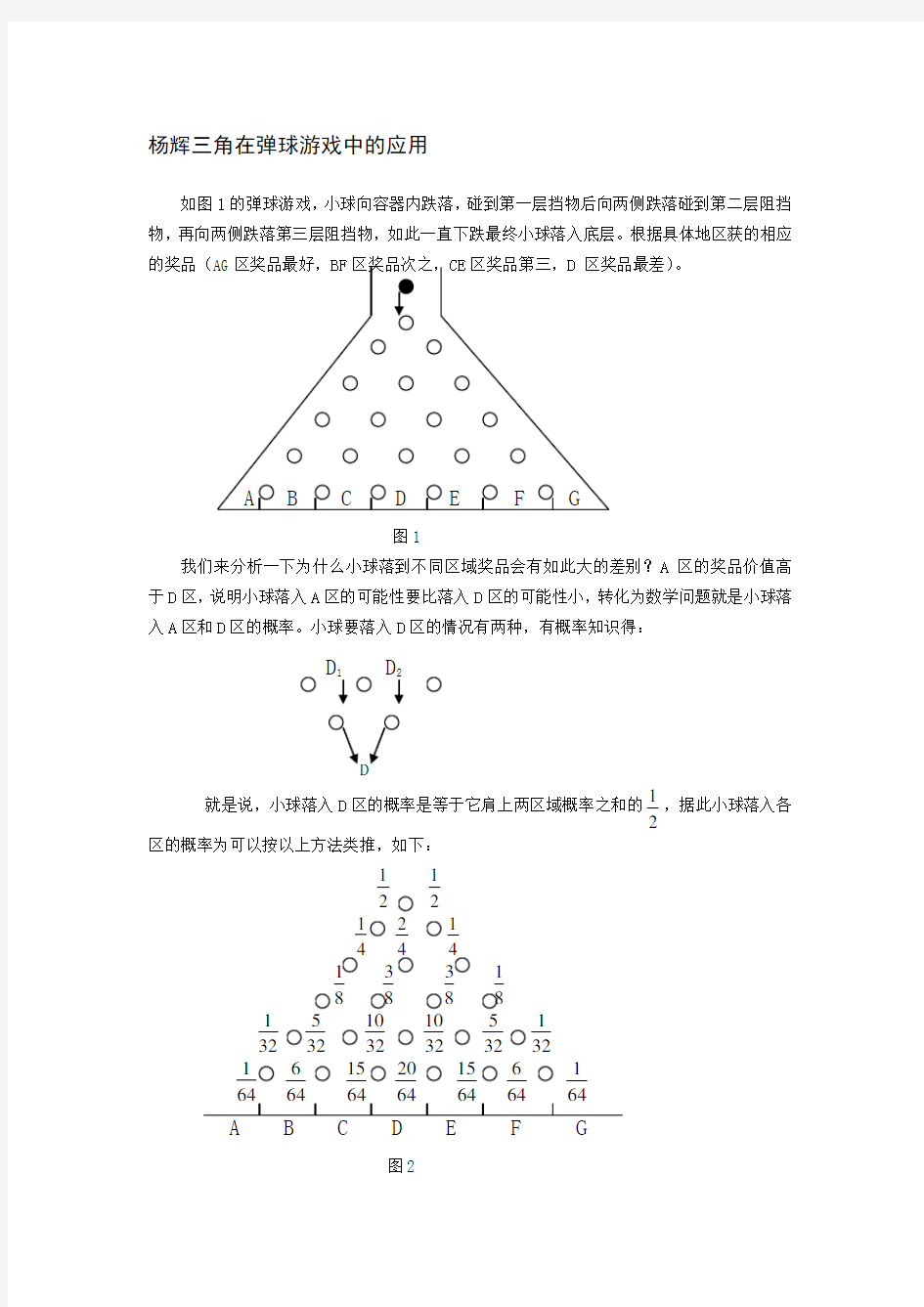
杨辉三角在弹球游戏中的应用
如图1的弹球游戏,小球向容器内跌落,碰到第一层挡物后向两侧跌落碰到第二层阻挡物,再向两侧跌落第三层阻挡物,如此一直下跌最终小球落入底层。根据具体地区获的相应的奖品(。
图1
我们来分析一下为什么小球落到不同区域奖品会有如此大的差别?A 区的奖品价值高于D 区,说明小球落入A 区的可能性要比落入D 区的可能性小,转化为数学问题就是小球落入A 区和D 区的概率。小球要落入D 区的情况有两种,有概率知识得:
D 1 D 2
就是说,小球落入D 区的概率是等于它肩上两区域概率之和的
2
1,据此小球落入各区的概率为可以按以上方法类推,如下: 2121
1
8381
3213232323232
1
64646641564206415646641 A B C D E F G
图2
观察上图,小球落到AD两区的概率要比其它区域小的多,当然奖品就要多一些。从该图中不难发现各区域的概率分子与杨辉三角形完全一致,我们可以利用杨辉三角的性质直接得出小球落到AD两区的概率要比其它区域小的多。
杨辉三角的规律以及定理 李博洋 摘要杨辉三角中的一些规律 关键词杨辉三角幂二项式 引言 杨辉是我国南宋末年的一位杰出的数学家。在他所着的《详解九章算法》一书 中,画了一张表示二项式展开后的系数构成的三角图形,称做“开方做法本源”,现 在简称为“杨辉三角”,它是世界的一大重要研究成果。我们则来对“杨辉三角”的 规律进行探讨和研究。 内容 1二项式定理与杨辉三角 与杨辉三角联系最紧密的是二项式乘方展开式的系数规律,即。 杨辉三角我们首先从一个二次多项式(a+b)2的展开式来探讨。 由上式得出:(a+b)2=a2+2ab+b2此代数式的系数为:121 则(a+b)3的展开式是什么呢?答案为:a3+3a2b+3ab2+b3由此可发现,此代数式的系数 为:1331但似乎没有什么规律,所以让我们再来看看(a+b)4的展开式。 展开式为:a4+4a3b+6a2b2+4ab3+b4由此又可发现,代数式的系数为: 14641似乎发现了一些规律,就可以发现以下呈三角形的数列: 1(110) 11(111) 121(112) 1331(113)
14641(114) 15101051(115) 1615201561(116) 因此可得出二项式定理的公式为: (a+b)n=C(n,0)a^n*b^0+C(n,1)a^(n-1)*b^1+...+C(n,r)a^(n-r)*b^r...+C(n,n)a^0*b^n 因此,二项式定理与杨辉三角形是一对天然的数形趣遇,它把带进了。求二项式展开式系数的问题,实际上是一种组合数的计算问题。用系数来计算,称为“式算”;用杨辉三角形来计算,称作“图算”。 2杨辉三角的幂的关系 首先我们把杨辉三角的每一行分别相加,如下: 1(1) 11(1+1=2) 121(1+2+1=4) 1331(1+3+3+1=8) 14641(1+4+6+4+1=16) 15101051(1+5+10+10+5+1=32) 1615201561(1+6+15+20+15+6+1=64) …… 相加得到的数是1,2,4,8,16,32,64,…刚好是2的0,1,2,3,4,5,6,…次幂,即杨辉三角第n行中n个数之和等于2的n-1次幂 3杨辉三角中斜行和水平行之间的关系 (1) 1(2)n=1 11(3)n=2 121(4)n=3 1331(5)n=4
杨辉三角形规律 每行数字两边对称每行数字左右对称,由1开始逐渐变大,然后变小,回到1。 第n行的数字个数为n个。 第n行数字和为2^(n-1)。(2的(n-1)次方) 每个数字等于上一行的左右两个数字之和。可用此性质写出整个帕斯卡三角形。 将第2n+1行第1个数,跟第2n+2行第3个数、第2n+3行第5个数……连成一线,这些数的和是第2n个斐波那契数。将第2n行第2个数,跟第2n+1行第4个数、第2n+2行第6个数……这些数之和是第2n-1个斐波那契数。 第n行的第1个数为1,第二个数为1×(n-1),第三个数为1×(n-1)×(n-2)/2,第四个数为1×(n-1)×(n-2)/2×(n-3)/3…依此类推。 两个未知数和的n次方运算后的各项系数依次为杨辉三角的第(n+1)行
杨辉三角在弹球游戏中的应用 如图1的弹球游戏,小球向容器内跌落,碰到第一层挡物后向两侧跌落碰到第二层阻挡物,再向两侧跌落第三层阻挡物,如此一直下跌最终小球落入底层。根据具体地区获的相应的奖品(。 图1 我们来分析一下为什么小球落到不同区域奖品会有如此大的差别?A 区的奖品价值高于D 区,说明小球落入A 区的可能性要比落入D 区的可能性小,转化为数学问题就是小球落入A 区和D 区的概率。小球要落入D 区的情况有两种,有概率知识得: D 1 D 2 就是说,小球落入D 区的概率是等于它肩上两区域概率之和的 2 1,据此小球落入各区的概率为可以按以上方法类推,如下: 2121 1 8381 3213232323232 1 64646641564206415646641 A B C D E F G 图2
杨辉三角与二项式系数的性质 教学反思 本节课有以下几点值得一提: 一、目标定位准确 本节课,在充分挖掘教学内容的内在联系,了解学生已有知识基础,充分分析学情后,确定的教学目标:理解、领悟二项式系数性质;渗透数形结合和分类讨论思想;灵活有效地运用赋值法.应该说具有具体而又准确,科学而有效的特点.随着课堂的实践得到了落实,并且将“知识目标”、“能力目标”、“情感目标”融为一体. 教学目标基本符合学生“认识规律”,以递进的形式呈现:观察分析、归纳猜想、抽象概括,提炼上升;特殊——一般——特殊到一般…,课堂实践表明,这些目标,在师生共同努力及合作下是完全可以达到的. 二、突出主体地位 1.放手发动学生 把课堂还给学生,一直是课改的大方向,也是新课标的原动力之一. 还给学生什么呢?教师作了很好的诠释: 一是给“问题”,当然问题有预设的,也有生成的,符合从学生“思维最近发展区”出发这一根本教学原则. 二是给“时间”,这体现了教师的先进教学理念,即便是教学难点“中间项系数最大”这一组合数计算讨论过程仍由学生尝试. 当然,n=6,7时,离散型函数的图象起了直观引领,奠基的重要作用. 不为完成任务所累,不为主宰课堂所困. 三是给“机会”,让学生展示自主探索,合作交流的成果,极大地保护和激发了学生学习的热情和积极性,参与程度和激情得到了空前的提高. 2.彰显理性数学 本节课,无论是对称性,增减性(最大值),及二项式系数和的逐步生成,学生都能从“特殊到一般”的认识规律,归纳猜想到结论. 但数形结合的函数思想,组合数两个性质的运用,两个计数原理的巧妙“会师”,奇数项二项式系数和等于偶数项二项式系数和,反馈升华例示中赋值法再现. 这正是“数学演绎”、“理性数学”的精华,让学生找到内化和建构的多种途径.
1.3.2二项式系数的性质(第一课时) 学校:新塘中学 班级:高二A8班 教师:段建辉 ●教学目标 (一)知识与技能 1.二项式系数的性质:对称性,增减性与最大值,各二项式系数的和. 2.掌握“赋值法”,并会简单应用 (二)情感与价值观 1.树立由一般到特殊及特殊到一般的意识. 2.了解中国古代数学成就及地位............. ●教学重点:二项式系数的性质 ●教学难点:二项式系数的最大值的理解与二项展开式中系数最大项有的求解. ●教学方法:发现法 ●授课类型:新授 ●教学情境设计: 一、复习回顾 1.二项式定理及其特例: (1)01()()n n n r n r r n n n n n n a b C a C a b C a b C b n N -*+=+++++∈L L , (2)1(1)1n r r n n n x C x C x x +=+++++L L . 2.二项展开式的通项公式:1r n r r r n T C a b -+= 二、引入 通项公式中的r n C ,我们称其为二项式系数.当n 依次取1,2,3…时, n b a )(+二项式系数,如下表所示:
表1 此表叫二项式系数表,早在南宋数学家杨辉所著的《详解九章算法》一书中出现了又叫杨辉三角.国外最早发现是在欧洲,叫帕斯卡三角,比中国晚了500年 下面我们可以利用“杨辉三角”来研究二项式系数的性质 三、探究 观察二项式系数表,根据提示的方法,寻找表中的规律. 【注意】 ?1)不要孤立的看、规律应该体现在联系之中 ?2)既要注意横向观察,也要注意纵向观察,横向观察是重点 ?3)可以结合函数图象或图表来研究,也可以和集合作联系 1、二项式系数表的规律 ①每行两端都是1 ②除1以外的每1个数都等于它肩上两个数的和(如何用数学知识解释?) 【提示】设这一数为r C 1-r n 和C r n ,由组合数知识可知: 1 1 01C C 02 C 12 C 2 2C 03 C 13 C 23 C 33 C 1 4C 0 4 C 3 4C 2 4C 4 4C 0 5C 1 5C 2 5C 35 C 4 5C 55 C
精心整理 杨辉三角的规律以及定理 二项式定理与杨辉三角1与杨辉三角联系最紧密的是二项式乘方展开式的系数规律,即二项式定理。 2的展开式来探讨。杨辉三角我们首先从一个二次多项式(a+b)222此代数式的系数为:121 由上式得出:(a+b)+2ab+b=由此可发现,此代数式的系+3+b+3ab(a+b 的展开式是什么呢?答案为(a+b的展开式。为133但似乎没有什么规律,所以让我们再来看b2+4a展开式为由此又可发现,代数式的系数为+4+b+6464似乎发现了一些规律,就可以发现以下呈三角形的数列:1 ) 1(1)11(112) 121(113) 1331(114) 14641(115) 15101051(116) 1615201561(11)1,4,6,4,1,(,1,2,1)(1,3,3,1)1,杨辉三角形的系数分别为:(1,1),(:所以(),1,7,21,35,35,21,7,1) (1,5,10,10,5,1),(1,6,15,20,15,6,17642547765233 (a+b)=ab+7ab+21a+bb+35a+7abb+35a。b+21a n的次数依次上b-n,n-n 等于a的次数依次下降、n-1、2...n由上式可以看出,(a+b) (2) 方。系数是杨辉三角里的系数。、、升,01 杨辉三角的幂的关系2 精心整理.
精心整理 首先我们把杨辉三角的每一行分别相加,如下: 1(1) 11(1+1=2) 121(1+2+1=4) 1331(1+3+3+1=8) 14641(1+4+6+4+1=16) 15101051(1+5+10+10+5+1=32) 1615201561(1+6+15+20+15+6+1=64) … 相加得到的数136…刚好,6,…次幂,即杨辉三角行个数之和等n-次 杨辉三角中斜行和水平行之间的关 (1) 1(2)n=1 11(3)n=2 121(4)n=3 1331(5)n=4 14641(6)n=5 15101051n=6 1615201561 把斜行(1)中第7行之前的数字相加得1+1+1+1+1+1+1=6
1. 3.2“杨辉三角”与二项式系数的性质 教学目标: 知识与技能:掌握二项式系数的四个性质。 过程与方法:培养观察发现,抽象概括及分析解决问题的能力。 情感、态度与价值观:要启发学生认真分析书本图1-5-1提供的信息,从特殊到一般,归纳猜想,合情推理得到二项式系数的性质再给出严格的证明。 教学重点:如何灵活运用展开式、通项公式、二项式系数的性质解题教学难点:如何灵活运用展开式、通项公式、二项式系数的性质解题授课类型:新授课 教 具:多媒体、实物投影仪 第一课时 一、复习引入: 1.二项式定理及其特例: (1)01()()n n n r n r r n n n n n n a b C a C a b C a b C b n N -*+=+++++∈, (2)1 (1)1n r r n n n x C x C x x +=++ ++ +. 2.二项展开式的通项公式:1r n r r r n T C a b -+= 3.求常数项、有理项和系数最大的项时,要根据通项公式讨论对r 的限制;求有理项时要注意到指数及项数的整数性 二、讲解新课: 1二项式系数表(杨辉三角) ()n a b +展开式的二项式系数,当n 依次取1,2,3…时,二项式系数 表,表中每行两端都是1,除1以外的每一个数都等于它肩上两个数的和 2.二项式系数的性质: ()n a b +展开式的二项式系数是0n C ,1n C ,2n C ,…,n n C .r n C 可以看成 以r 为自变量的函数()f r 定义域是{0,1,2, ,}n ,例当6n =时,其图象是7个孤立的点(如图) (1)对称性.与首末两端“等距离”的两个二项式系数相等 (∵m n m n n C C -=). 直线2 n r = 是图象的对称轴. (2)增减性与最大值.∵1(1)(2)(1)1!k k n n n n n n k n k C C k k ----+-+= =? ,
/* Name: 杨辉三角算法集锦 Copyright: 始发于goal00001111的专栏;允许自由转载,但必须注明作者和出处Author: goal00001111 Date: 27-11-08 19:04 Description: 分别使用了二维数组,一维数组,队列,二项式公式,组合公式推论和递归方法等9种算法 算法思路详见代码注释——注释很详细,呵呵 */ #include
cout << endl; Fun_6(row); cout << endl; Fun_7(row); cout << endl; Fun_8(row); cout << endl; Fun_9(row); system("pause"); return 0; } //输出n个空格 void PrintBlank(int n) { for (int i=0; i 杨辉三角的规律以及定理 1 二项式定理与杨辉三角 与杨辉三角联系最紧密的是二项式乘方展开式的系数规律,即二项式定理。 杨辉三角我们首先从一个二次多项式 (a+b) 2 的展开式来探讨。 由上式得出: (a+b) 2= a 2+2ab+b 2 此代数式的系数为: 1 2 1 则 (a+b) 3 的展开式是什么呢?答案为: a 3+3a 2b+3a b 2+b 3 由此可发现, 此代数式的系数为: 1 3 3 1 但 似乎没有什么规律,所以让我们再来看看 (a+b) 4 的展开式。 展开式为: a 4 +4a 3b+6a 2b2+4ab 3+b 4 由此又可发现,代数式的系数为: 1 4641 似乎发现了一些规律,就可以发现以下呈三角形的数列: 1 (11 ) 1 1 (11 1 ) 1 2 1 (11 2 ) 1 3 3 1 (11 3 ) 1 4 6 4 1 (11 4 ) 1 5 10 10 5 1 (11 5 ) 1 6 15 20 15 6 1 (11 6) 杨辉三角形的系数分别为: 1,(1,1 ),(1,2,1 ),( 1,3,3,1 ),( 1,4,6,4,1 )( 1,5,10,10,5,1 ),( 1,6,15,20,15,6,1 ), ( 1,7,21,35,35,21,7,1)所以: (a+b) 7=a 7+7a 6 b+21a 5b 2+35a 4b 3+35a 3b 4+21a 2b 5+7ab 6+b 7。 由上式可以看出, (a+b) n 等于 a 的次数依次下降 n 、n-1 、n- 2?n -n ,b 的次数依次上升, 0、1、2?n 次方。系数是 杨辉三角里的系数。 2 杨辉三角的幂的关系 首先我们把杨辉三角的每一行分别相加,如下: 1 ( 1 ) 1 1 ( 1+1=2 ) 1 2 1 (1+2+1=4 ) 1 3 3 1 (1+3+3+1=8 ) 1 4 6 4 1 (1+4+6+4+1=16 ) 1 5 10 10 5 1 (1+5+10+10+5+1=3 2 ) 1 6 15 20 15 6 1 (1+6+15+20+15+6+1=64 ) ?? 相加得到的数是 1, 2, 4, 8, 16, 32, 64,?刚好是 2 的 0, 1,2, 3, 4, 5, 6,? n 次幂,即杨辉三角第 n 行中 n 个数之和等于 2 的 n-1 次幂 3 杨辉三角中斜行和水平行之间的关系 杨辉三角的规律以及定理 1二项式定理与杨辉三角 杨辉三角我们首先从一个二次多项式(a+b)2的展开式来探讨。 由上式得出:(a+b)2=a2+2ab+b2此代数式的系数为: 1 2 1 则(a+b)3的展开式是什么呢?答案为:a3+3a2b+3ab2+b3由此可发现,此代数式的系数为: 1 3 3 1 但似乎没有什么规律,所以让我们再来看看(a+b)4的展开式。 展开式为:a4+4a3b+6a2b2+4ab3+b4由此又可发现,代数式的系数为: 1 4 6 4 1 似乎发现了一些规律,就可以发现以下呈三角形的数列: 1 (110) 1 1 (111) 1 2 1 (112) 1 3 3 1 (113) 1 4 6 4 1 (114) 1 5 10 10 5 1 (115) 1 6 15 20 15 6 1 (116) 杨辉三角形的系数分别为:1,(1,1),(1,2,1),(1,3,3,1),(1,4,6,4,1)(1,5,10,10,5,1),(1,6,15,20,15,6,1),(1,7,21,35,35,21,7,1)所以:(a+b)7=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7。 由上式可以看出,(a+b)n等于a的次数依次下降n、n-1、n-2…n-n,b的次数依次上升,0、1、2…n次方。系数是杨辉三角里的系数。 2杨辉三角的幂的关系 首先我们把杨辉三角的每一行分别相加,如下: 1 ( 1 ) 1 1 ( 1+1= 2 ) 1 2 1 (1+2+1=4 ) 1 3 3 1 (1+3+3+1=8 ) 1 4 6 4 1 (1+4+6+4+1=16 ) 1 5 10 10 5 1 (1+5+10+10+5+1=3 2 ) 1 6 15 20 15 6 1 (1+6+15+20+15+6+1=64 ) …… 相加得到的数是1,2,4,8,16,32,64,…刚好是2的0,1,2,3,4,5,6,…n次幂,即杨辉三角第n 行中n个数之和等于2的n-1次幂 3 杨辉三角中斜行和水平行之间的关系 2019-2020学年高一数学 杨辉三角与二项式系数(二)作业 1.(a+b)n 展开式中第四项与第六项的系数相等,则n 为( ) A .8 B .9 C .10 D .11 2.二项式(1-x)4n+1的展开式系数最大的项是( ) A .第2n+1项 B .第2n+2项 C .第2n 项 D 第2n+1项或2n+2项 3.10110-1的末尾连续零的个数是( ) A .1个 B .2个 C .3个 D .4个 4.若n 为奇数,777712211---+???+++n n n n n n n C C C 被9除所得的余数是( ) A .0 B .2 C .7 D .8 5.5 n +13 n (n N ∈)除以3的余数是( ) A .0 B .0或1 C .0或2 D .2 6.数(1.05)6的计算结果精确到0.01的近似值是( ) A .1.23 B .1.24 C .1.33 D .1.44 7.!20123181920!417181920!21920C 0 4?????????+???+???+?+ 的值是( ) A .217 B .218 C .219 D .220 8.(1-2x)15的展开式中的各项系数和是( ) A .1 B .-1 C .215 D .315 9. 在(ax+1)7的展开式中,(a>1),x 3的系数是x 2的系数与x 4的系数的等差中项,则a 的值是 。 10.设112131)13(x x + 展开式中各项系数和为A ,而它的二项式系数之和为B ,若A+B=272,那么展开式中x 2项的系数是 。 11.关于二项式(x 1)2007有下列四个命题: ①该二项展开式中非常数项的系数和是1; ②该二项展开式中系数最大的项是第1004项; ③该二项展开式中第6项为200162007x C ; ④当x=2008时,(x 1)2007 除以2008的余数是2007。 其中正确命题的序号是 。 12.将杨辉三角中的奇数换成1,偶数换成0,得到如下图所示的01三角数表,从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n 行全行的数都为1的是第 行。 第1行 1 1 第2行 1 0 1 第3行 1 1 1 1 第4行 1 0 0 0 1 第5行 1 1 0 0 1 1 …… ……… ……… ……… 13.用二项式定理证明6363+17能被16整除. 杨辉三角的规律以及定理 1 二项式定理与杨辉三角 与杨辉三角联系最紧密的是二项式乘方展开式的系数规律,即二项式定理。 杨辉三角我们首先从一个二次多项式 (a+b) 2 的展开式来探讨。 由上式得出: (a+b) 2 2+2ab+b 2 =a 此代数式的系数为: 1 2 1 则(a+b) 3 3+3a 2b+3ab 2+b 3 的展开式是什么呢?答案为: a 由此可发现, 此代数式的系数为: 1 3 3 1 但 4 似乎没有什么规律,所以让我们再来看看 (a+b) 的展开式。 展开式为: a 4+4a 3b+6a 2b2+4ab 3+b 4+4a 3b+6a 2b2+4ab 3+b 4 由此又可发现,代数式的系数为: 1 4 6 4 1 似乎发现了一些规律,就可以发现以下呈三角形的数列: 1 (11 0) 1 1 (11 1) 1 2 1 (11 2) 1 3 3 1 (11 3) 1 4 6 4 1 (11 4) 1 5 10 10 5 1 (11 5 ) 1 6 15 20 15 6 1 (11 6) 杨辉三角形的系数分别为: 1,(1,1 ),(1,2,1 ),(1,3,3,1 ),(1,4,6,4,1 )(1,5,10,10,5,1 ),(1,6,15,20,15,6,1 ), (1,7,21,35,35,21,7,1 )所以: (a+b) 7=a 7+7a 6 b+21a 5b 2+35a 4b 3+35a 3b 4+21a 2b 5+7ab 6+b 7。 由上式可以看出, (a+b) n 等于 a 的次数依次下降 n 、n-1 、n- 2? n -n ,b 的次数依次上升, 0、1、2? n 次方。系数是 杨辉三角里的系数。 2 杨辉三角的幂的关系 首先我们把杨辉三角的每一行分别相加,如下: 1 ( 1 ) 1 1 ( 1+1= 2 ) 1 2 1 (1+2+1=4 ) 1 3 3 1 (1+3+3+1=8 ) 1 4 6 4 1 (1+4+6+4+1=16 ) 1 5 10 10 5 1 (1+5+10+10+5+1=3 2 ) 1 6 15 20 15 6 1 (1+6+15+20+15+6+1=64 ) ? ? 相加得到的数是 1,2, 4,8,16,32, 64,? 刚好是 2 的 0,1,2,3,4,5, 6,? n 次幂,即杨辉三角第n 行中 n 个数之和等于 2 的 n-1 次幂 3 杨辉三角中斜行和水平行之间的关系 河北省二十冶综合学校高中分校高考数学总复习 杨辉三角与 二项式系数的性质教案 教学目标:掌握二项式系数的四个性质。 教学重点:如何灵活运用展开式、通项公式、二项式系数的性质解题。 教学难点:如何灵活运用展开式、通项公式、二项式系数的性质解题。 一,复习1.二项式定理及其特例: (1)01()()n n n r n r r n n n n n n a b C a C a b C a b C b n N -*+=+++++∈, (2)1(1)1n r r n n n x C x C x x +=+++++. 2.二项展开式的通项公式: 二、讲解新课: 1二项式系数表(杨辉三角) 课本32页探 究: ,。 2.二项式系数的性质: ()n a b +展开式的二项式系数是0n C ,1n C ,2n C ,…,n n C .r n C 可以看成以r 为自变 量的函数()f r 定义域是{0,1,2,,}n ,例当6n =时,其图象是7个孤立的点(如图) (1)对称性: , 。 (2)增减性与最大值: , . . (3)各二项式系数和: ∵1(1)1n r r n n n x C x C x x +=+++++, 令 ,则0122n r n n n n n n C C C C C =+++ +++ 三,课堂小练 (1)20)(b a +第 项的二项式系数最大,最大是 。 (2)19)(b a +第 项的二项式系数最大,最大是 。 (3)n x )21(+的展开式中第5项与第8项的二项式系数相等,求展开式中二项式系数最大的项是 。 注意:二项式系数最大的项不一定是系数最大的项。 (4)=++++77372717C C C C 。 三、讲解范例: 例1.在()n a b +的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和 说明:由性质(3)及例1知021312n n n n n C C C C -++=++=. 例2.已知7270127(12)x a a x a x a x -=++++,求: 杨辉三角的规律以及推 导公式 HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】 杨辉三角的规律以及定理 李博洋 摘要杨辉三角中的一些规律 关键词杨辉三角幂二项式 引言 杨辉是我国南宋末年的一位杰出的数学家。在他所着的《详解九章算法》一书中,画了一张表示二项式展开后的系数构成的三角图形,称做“开方做法本源”,现在简称为“杨辉三角”,它是世界的一大重要研究成果。我们则来对“杨辉三角”的规律进行探讨和研究。 内容 1二项式定理与杨辉三角 杨辉三角我们首先从一个二次多项式(a+b)2的展开式来探讨。 由上式得出: (a+b)2=a2+2ab+b2此代数式的系数为: 1 2 1 则(a+b)3的展开式是什么呢?答案为:a3+3a2b+3ab2+b3由此可发现,此代数式的系数为: 1 3 3 1 但似乎没有什么规律,所以让我们再来看看(a+b)4的展开式。 展开式为:a4+4a3b+6a2b2+4ab3+b4由此又可发现,代数式的系数为: 1 4 6 4 1 似乎发现了一些规律,就可以发现以下呈三角形的数列: 1 (110) 1 1 (111) 1 2 1 (112) 1 3 3 1 (113) 1 4 6 4 1 (114) 1 5 10 10 5 1 (115) 1 6 15 20 15 6 1 (116) 因此可得出二项式定理的公式为:(a+b)n=C(n,0)a^n*b^0+C(n,1)a^(n- 1)*b^1+...+C(n,r)a^(n-r)*b^r...+C(n,n)a^0*b^n 因此,二项式定理与杨辉三角形是一对天然的数形趣遇,它把数形结合带进了计算数学。求二项式展开式系数的问题,实际上是一种组合数的计算问题。用系数通项公式来计算,称为“式算”;用杨辉三角形来计算,称作“图算”。 2杨辉三角的幂的关系 首先我们把杨辉三角的每一行分别相加,如下: 1 ( 1 ) 二项式系数的性质(第一课时) 学校:新塘中学 班级:高二A8班 教师:段建辉 ●教学目标 (一)知识与技能 1.二项式系数的性质:对称性,增减性与最大值,各二项式系数的和. 2.掌握“赋值法”,并会简单应用 (二)情感与价值观 1.树立由一般到特殊及特殊到一般的意识. 2.了解中国古代数学成就及地位............. ●教学重点:二项式系数的性质 ●教学难点:二项式系数的最大值的理解与二项展开式中系数最大项有的求解. ●教学方法:发现法 ●授课类型:新授 ●教学情境设计: 一、复习回顾 1.二项式定理及其特例: (1)01()()n n n r n r r n n n n n n a b C a C a b C a b C b n N -*+=+++++∈L L , (2)1(1)1n r r n n n x C x C x x +=+++++L L . 2.二项展开式的通项公式:1r n r r r n T C a b -+= 二、引入 通项公式中的r n C ,我们称其为二项式系数.当n 依次取1,2,3…时, n b a )(+二项式系数,如下表所示: 表1 此表叫二项式系数表,早在南宋数学家杨辉所著的《详解九章算法》一书中出现了又叫杨辉三角.国外最早发现是在欧洲,叫帕斯卡三角,比中国晚了500年 11 01C C 02 C 12 C 2 2C 0 3 C 13 C 23 C 33 C 1 4C 0 4 C 3 4C 2 4C 4 4C 05 C 15 C 25 C 35 C 45 C 55 C 下面我们可以利用“杨辉三角”来研究二项式系数的性质 三、探究 观察二项式系数表,根据提示的方法,寻找表中的规律. 【注意】 ?1)不要孤立的看、规律应该体现在联系之中 ?2)既要注意横向观察,也要注意纵向观察,横向观察是重点 ?3)可以结合函数图象或图表来研究,也可以和集合作联系 1、二项式系数表的规律 ①每行两端都是1 ②除1以外的每1个数都等于它肩上两个数的和(如何用数学知识解释) 【提示】设这一数为 r C 1-r n 和C r n ,由组合数知识可知: ③与首末两端“等距离”的两个二项式系数相等 ④中间的数值最大 2、二项式系数的函数观点 n b a )(+展开式的二项式系数依次是:C n 0 , C n 1…C n r …C n n . 从函数角度看,r n C 可看成是以r 为自变量的函数)(r f y = 其定义域是:{0,1,2…n } 当n=5及n=6时,分别作出其图象 图1 图2 据图可分析出函数r n C r f =)(,图象的对称轴是2 n r = 3、二项式系数的性质 据图1,2和表1可得出二项式系数的性质 【1】对称性 与首末两端“等距离”的两个二项式系数相等(∵m n m n n C C -=). 直线2 n r = 是图象的对称轴. [典型问题] .已知5 15C =a ,9 15C =b ,那么10 16C =__________; “杨辉三角”与二项式系数的性质 学习目标: 1掌握二项式定理和二项式系数的性质。 2.能灵活运用展开式、通项公式、二项式系数的性质解题 学习重点:如何灵活运用展开式、通项公式、二项式系数的性质解题 学习难点:如何灵活运用展开式、通项公式、二项式系数的性质解题 授课类型:新授课 课时安排:1课时 教具:多媒体、实物投影仪 教学过程: 一、复习引入: 1.二项式定理及其特例: (1), (2). 2.二项展开式的通项公式: 3.求常数项、有理项和系数最大的项时,要根据通项公式讨论 对的限制;求有理项时要注意到指数及项数的整数性 41二项式系数表(杨辉三角) 展开式的二项式系数,当依次取…时,二项式 系数表,表中每行两端都是,除以外的每一个数都等于它肩上两个数的和 5.二项式系数的性质: 展开式的二项式系数是,,,…,.可以看成以为自变量的函数,定义域是,例当时,其图象是个孤立的点(如图) (1)对称性.与首末两端“等距离”的两个二项式系数相等(∵). 直线是图象的对称轴. (2)增减性与最大值:当是偶数时,中间一项取得最大值;当是奇数时,中间两 项,取得最大值. (3)各二项式系数和: ∵, 令,则 二、讲解范例: 例1.设, 当时,求的值 解:令得: , ∴, 点评:对于,令即可得各项系数的和的值;令即,可得奇数项系数和与偶数项和的关系 例2.求证:. 证(法一)倒序相加:设① 又∵② ∵,∴, 由①+②得:, ∴,即. (法二):左边各组合数的通项为 , ∴. 例3.已知:的展开式中,各项系数和比它的二项式系数和大. (1)求展开式中二项式系数最大的项;(2)求展开式中系数最大的项 解:令,则展开式中各项系数和为, 又展开式中二项式系数和为, ∴,. (1)∵,展开式共项,二项式系数最大的项为第三、四两项, ∴,, (2)设展开式中第项系数最大,则, ∴,∴, 即展开式中第项系数最大,. 例4.已知, 求证:当为偶数时,能被整除 分析:由二项式定理的逆用化简,再把变形,化为含有因数的多项式∵, ∴,∵为偶数,∴设(), ∴ (), 当=时,显然能被整除, 当时,()式能被整除, 所以,当为偶数时,能被整除 1.3.2杨辉三角与二项式系数的性质(二) 班级 姓名 1.(a+b)n 展开式中第四项与第六项的系数相等,则n 为( ) A .8 B .9 C .10 D .11 2.二项式(1-x)4n+1的展开式系数最大的项是( ) A .第2n+1项 B .第2n+2项 C .第2n 项 D 第2n+1项或2n+2项 3.10110-1的末尾连续零的个数是( ) A .1个 B .2个 C .3个 D .4个 4.若n 为奇数,77771221 1---+???+++n n n n n n n C C C 被9除所得的余数是 ( ) A .0 B .2 C .7 D .8 5.5 n +13 n (n N ∈)除以3的余数是( ) A .0 B .0或1 C .0或2 D .2 6.数(1.05)6的计算结果精确到0.01的近似值是( ) A .1.23 B .1.24 C .1.33 D .1.44 7.! 201 23181920!417181920!21920C 0 4?????????+ ???+???+?+ 的值是( ) A .217 B .218 C .219 D .220 8.(12x)15的展开式中的各项系数和是( ) A .1 B .-1 C .215 D .315 9. 在(ax+1)7的展开式中,(a>1),x 3的系数是x 2的系数与x 4的系数的等差中项,则a 的值是 。 10.设11 2 1 3 1)1 3(x x + 展开式中各项系数和为A ,而它的二项式系数之和为B ,若A+B=272,那么展开式中x 2项的系数是 。 11.关于二项式(x 1)2007有下列四个命题: ①该二项展开式中非常数项的系数和是1; ②该二项展开式中系数最大的项是第1004项; ③该二项展开式中第6项为2001 62007x C ; ④当x=2008时,(x 1)2007除以2008的余数是2007。 其中正确命题的序号是 。 12.将杨辉三角中的奇数换成1,偶数换成0,得到如下图所示的01三角数表,从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n 行全行的数都为1的是第 行。 第1行 1 1 第2行 1 0 1 第3行 1 1 1 1 第4行 1 0 0 0 1 第5行 1 1 0 0 1 1 …… ……… ……… ……… 13.用二项式定理证明6363+17能被16整除. 数学家杨辉 杨辉,中国南宋末年杰出的数学家和数学教育家。在13世纪中叶活动于苏杭 一带,其著作甚多。 他著名的数学书共五种二十一卷。著有《详解九章算法》十二卷(1261年)、《日用算法》二卷(1262年)、《乘除通变本末》三卷(1274年)、《田亩比类乘除算法》二卷(1275年)、《续古摘奇算法》二卷(1275年)。 其中在《详解九章算法》一书中载有二项(a+b)n展开系数的数字三角形,被称为“杨辉三角”,它的发现比国外同类发现至少早3O0年。 杨辉的数学研究与教育工作的重点是在计算技术方面,他对筹算乘除捷算法进行总结和发展,有的还编成了歌决,如九归口决。 他在《续古摘奇算法》中介绍了各种形式的"纵横图"及有关的构造方法,同时"垛积术"是杨辉继沈括"隙积术"后,关于高阶等差级数的研究。杨辉在"纂类"中,将《九章算术》246个题目按解题方法由浅入深的顺序,重新分为乘除、分率、合率、互换、二衰分、叠积、盈不足、方程、勾股等九类。 他非常重视数学教育的普及和发展,在《算法通变本末》中,杨辉为初学者制订的"习算纲目"是中国数学教育史上的重要文献。 ================================================================= 杨辉介绍 杨辉,字谦光,中国南宋(1127~1279)末年钱塘(今杭州市)人。其生卒年月及生平事迹均无从详考。据有关著述中的字句推测,杨辉大约于13世纪中叶至末叶生活在现今浙江杭州一带,曾当过地方官,到过苏州、台州等地。是当时有名的数学家和数学教育家,他每到一处都会有人慕名前来请教数学问题。 杨辉一生编写的数学书很多,但散佚也很严重。据史料记载,他至少有以下书,曾在国内或国外刊行: 《详解九章算法》12卷(1261) 精心整理杨辉三角的规律以及定理 1二项式定理与杨辉三角 杨辉三角我们首先从一个二次多项式(a+b)2的展开式来探讨。 222 则 为: 1 1(11 )(1,5,10,10,5,1),(1,6,15,20,15,6,1),(1,7,21,35,35,21,7,1)所以:(a+b)7=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7。 由上式可以看出,(a+b)n等于a的次数依次下降n、n-1、n-2…n-n,b的次数依次上升,0、1、2…n次方。系数是杨辉三角里的系数。 2杨辉三角的幂的关系 首先我们把杨辉三角的每一行分别相加,如下: 1(1) 11(1+1=2) 121(1+2+1=4) 1331(1+3+3+1=8) 6,…n 3 1615201561 把斜行(1)中第7行之前的数字相加得1+1+1+1+1+1+1=6 把斜行(2)中第7行之前的数字相加得1+2+3+4+5=15 把斜行(3)中第7行之前的数字相加得1+3+6+10=20 把斜行(4)中第7行之前的数字相加得1+4+10=15 把斜行(5)中第7行之前的数字相加得1+5=6 把斜行(6)中第7行之前的数字相加得1 将上面得到的数字与杨辉三角中的第7行中的数字对比,我们发现它们是完全 相同的。 n (3)中第 2、每行数字左右对称,由1开始逐渐变大。 3、第n行的数字有n+1项。 4、第n行数字和为2(n-1)。(2的(n-1)次方) 5 (a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。 [1] 6、第n行的第m个数和第n-m个数相等,即C(n,m)=C(n,n-m),这是组合数性质 杨辉三角考题赏析 “杨辉三角”是我国古代数学的瑰宝.利用杨辉三角不仅讨论了二项展开式的一些性质,杨辉三角本身还包含着许多有趣的规律和性质.正因为如此,以“杨辉三角”为背景的试题在近年的高考或各地模拟题中频频出现,有力地考查了同学们对数据的整理、分析、概括、处理能力和创新思维能力.现采撷几例,与同学们共赏析. 例1 (2004年上海春季高考卷)如图1,在由二项式系数所构成的杨辉三角中,第_____行中从左到右第14与第15个数的比为2:3. 解析:由图1我们能发现,第1行中的数是0111C C ,;第2行中的数是 012222C C C ,,;第3行中的数是01233333C C C C ,,,; ;则第n 行中的数是 012n n n n n C C C C ,,,,设第n 行中从左到右第14与第15个数的比为2:3,则 13142:3n n C C =·,解得34n =. 点评:本题是关于“杨辉三角”的一道高考题.杨辉三角中蕴含着许多有趣的数量关系,与排列、组合和概率的关系非常密切.因此,理解和掌握杨辉三角的一些性质,对发现某些数学规律是很有帮 助的. 例2 (2006届全国100所名校示范卷)如图2所示,在杨辉三角中,斜线 AB 上方箭头所示的数组成一个锯齿形的数列:1,2,3,3,6,4,10, ,记 这个数列的前n 项的和为()S n ,则(16)S 等于( ). A .144 B .146 C .164 D .461 解析:由图2知,数列中的首项是22C ,第2项是1 2C ,第3项是23C ,第4项 是13C ,,第15项是29C ,第16项是1 9C . 因此得121 21211 1223399239(16)()S C C C C C C C C C =++++++=+++2 22239()C C C ++++ 21 123 2223 33923391010()()1164C C C C C C C C C =+++-++++==+-=.故选C. 点评:本题是杨辉三角与数列结合的一道考题.将数列的各项还原为各二项展开式的二项式系数,并依次应用杨辉三角中数的规律Crn+1=Cr-1n+Crn (即组合数性质2),从而求得数列的和. 例3 (2004年江苏高考模拟卷)观察下列数表,问此表最后一个数是 什么,并说明理由. 解析:因为第一行有100个数,以后每一行都比前一行少一个数,因此共有100行. 通过观察可以得到: 第1行首尾两项之和为101; 第2行首尾两项之和为1012?; 第3行首尾两项之和为21012?, 第4行首尾两项之和为31012?,…… 第99行首尾两项之和为981012?. 因为从第2行开始每一个数字是它肩上两个数字之和,所以最后一个数字即第100行的数字是它肩上第99行首尾两个数字之和即为981012?. 点评:本题是一道以“杨辉三角”为背景的一道考题.通过观察找出每一行数据间的相互联系以及行与行间数据的相互联系.然后对数据间的这种联系用数学式子将它表达出来,使问题得解.杨辉三角的规律以与推导公式-杨辉三角规律
杨辉三角的规律以及推导公式
2019-2020学年高一数学 杨辉三角与二项式系数(二)作业.doc
杨辉三角的规律以及推导公式-杨辉三角规律
高考数学总复习 杨辉三角与二项式系数的性质教案
杨辉三角的规律以及推导公式定稿版
教学案例.杨辉三角与二项式系数性质
杨辉三角与二项式系数的性质 说课稿 教案 教学设计
1.3.2杨辉三角与二项式系数(二)作业
杨辉与杨辉三角
杨辉三角的规律以及推导公式
杨辉三角考题阅读