
偏微分方程数值解上机实习
数值求解二维扩散方程的初边值问题
22
22(,,0)sin sin 2(0,,)(1,,)1
(,0,)(,1,)1
u u u
t x y
u x y x y u y t u y t u x t u x t ππ????=+??????
=??==??==?
(0,1,0)(0,1)(01,0)
(01,0)x y t x y y t x t <<><<<<≥<<≥ 古典显式格式:
1,,1,,1,,1,,1
2
2
22n n
n n n
n n n
j l j l
j l j l j l
j l j l j l u u u u u u u u h
h
τ
++-+---+-+=
+
将原格式化为:1
2
,1,1,,1,1,(14),/n n
n
n n
n
j l j l j l j l j l j l u u u u u u h λλλλλλτ++-+-=++++-=其中 附源程序:
%-------------------------------------------运用古典显式差分格式求解二维扩散方程的初边值问题; function gdxs(ti,h,t)
%-------------------------------------------ti:时间步长; %-------------------------------------------h:空间步长; k=t/ti;
m=1/h+1;
r=ti/h^2; %------------------------------ r 为网格比; w=ones(m,m); u=ones(m,m); for i=2:m-1
for j=2:m-1
u(i,j)=sin(pi*(i-1)*h)*sin(2*pi*h*(j-1)); end end tic
for l=1:k
for i=2:m-1
for j=2:m-1
w(i,j)=r*u(i-1,j)+r*u(i,j-1)+r*u(i+1,j)+r*u(i,j+1)+(1-4*r)*u(i,j); end end u=w; end toc t=toc u
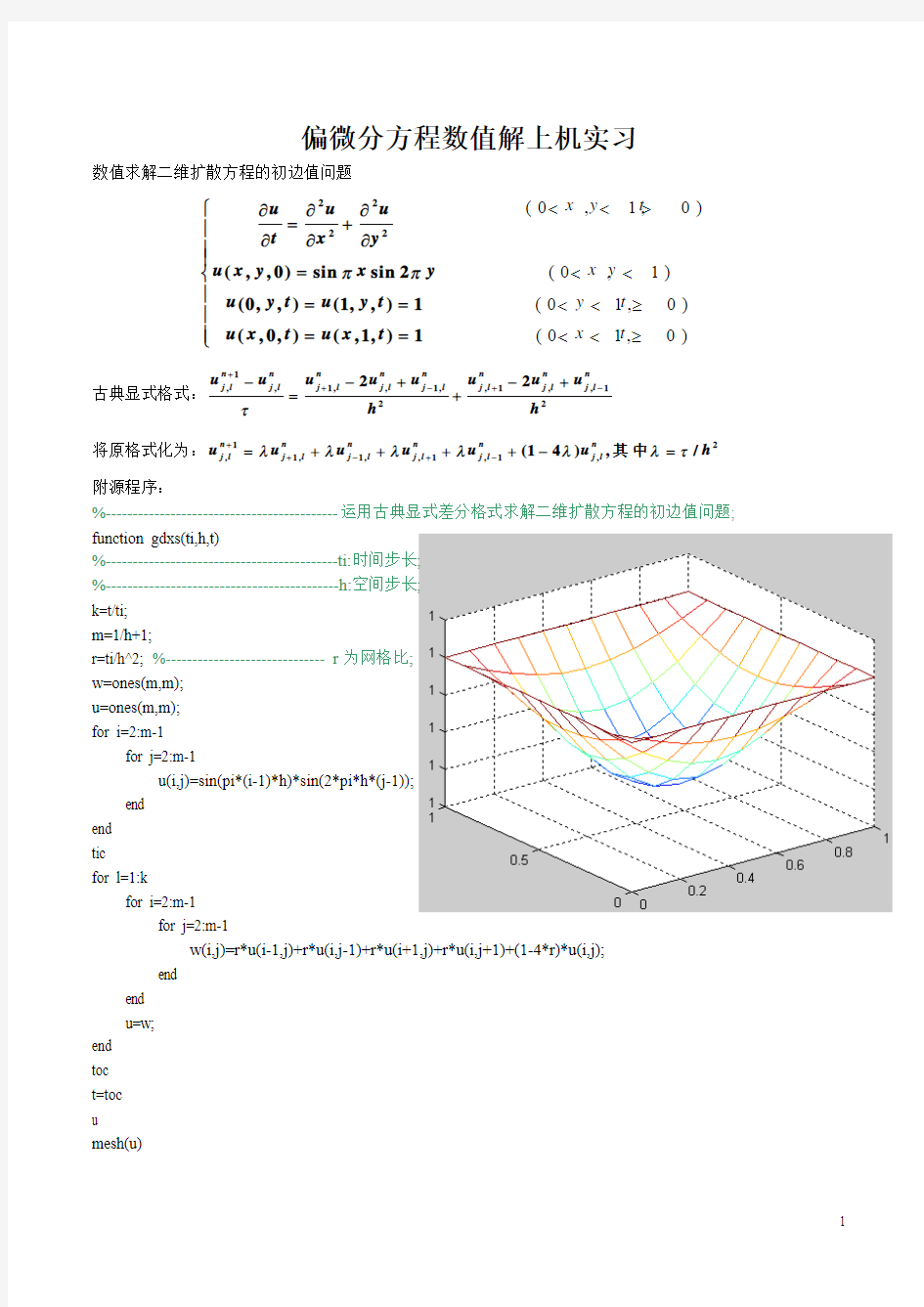
mesh(u)
交替方向隐式格式(P-R 格式):
1
111
2
222,,1,,1,,1,,1221111
1111222
2,,1,,1,,1,,122
222
222
n n n n n n n n j l j l j l j l j l j l j l j l n n n n n n n n j l j l j l j l j l j l j l j l u u u u u u u u h h
u u u u u u u u h h ττ+++++-+-++++
+++++-+-?--+-+?=+??
???--+-+?=+??? 将原差分格式化为:
111
222
1,,1,,1,,12
111
111222
,1,,11,,1,/n n n n n n j l j l j l j l j l j l n n n n n n j l j l j l j l j l j l
u u u u u u h u u u u u u λλλλλλλτλλλλλλ++++-+-+++
++++-+-?-+-=++?=??-+-=++?(2+2)(2-2),其中(2+2)(2-2) 121,,11
2
,22,1
,2,222222222222222222n n
l j n
n j l n j m n m l
u u u u u u λλλλλλ
λ
λλλλλ
λ
λ
λλ
λ
λλλλλ
λλλ
λ
λ+++??
???-+--??
?? ? ? ? ?-+-- ? ? ? ?
? ? ? ?= ? ? ? ? ? ? ? ? ? ?
? ?-+--?????? ? ???
-+-?-+--+-?
1
211,,1
1
12
,22,11
,2,222222n n l j n n j l n j m n m l
u u u
u u u λλλ
λλλ
λ
λ
λ++++++?????????????? ????-??? ? ?? ? ?- ? ?? ? ?
? ?? ?
?= ?
?? ? ? ? ?? ? ? ? ? ? ??-??
??? ?? ???
?
代入边界条件,转化为三对角矩阵
122,,21
2
,33,1
,121,2222222220022222222n n
l j n n j l n j m n m l
u u u u u u λλλλ
λλλλλλλ
λ
λλ
λλ
λλλ++-+-??
???+--??????
? ?
? ?
?-+-- ? ? ? ? ?
? ? ? ? ?=+ ? ? ? ? ? ? ? ? ? ?
? ?
? ? ?-+-??????
?? ? ???
+--+
1
212,,2
1
12
,33,11
,121,2222220022222n n l j n n j l n j m n m l
u u
u u u u λλ
λλλλλλ
λ
λλ
λλ+++++-+-?
????????????
?
????-????
?? ? ?
? ? ?-- ? ? ? ? ?
? ? ?
? ?=+ ? ? ? ? ? ? ? ? ? ?
? ? ? ? ?-+-???
???
?? ? ???
?
???????
附追赶法源程序:
%-------------------------------------------追赶法求解三对角方程组;
function x=zg(a,b,c,d)
%--------------------------------------------a:方程组系数矩阵A的下对角元素;
%--------------------------------------------b:方程组系数矩阵A的主对角元素;
%--------------------------------------------c:方程组系数矩阵A的上对角元素;
%--------------------------------------------d:追赶法所求方程的右端向量;
%--------------------------------------------l:系数矩阵A所分解成的下三角阵L中的下对角元素了l(i); %--------------------------------------------u:系数矩阵A所分解成的下三角阵U中的主对角元素了u(i); n=length(b);
u(1)=b(1);
y(1)=d(1);
for i=1:n-1 %--------------------------追赶法求解之追过程求解Ly=d;
l(i)=a(i)/u(i);
u(i+1)=b(i+1)-l(i)*c(i);
y(i+1)=d(i+1)-l(i)*y(i);
end
x(n)=y(n)/u(n); %------------------------追赶法求解之赶过程求解Uz=y;
for j=n-1:-1:1
if u(j)==0
break;
else
x(j)=(y(j)-c(j)*x(j+1))/u(j);
end
end
%-----------------------------------------------运用P-R差分格式求解二维扩散方程的初边值问题; function pr(ti,h,t)
%-------------------------------------------ti:时间步长h:空间步长;
k=t/ti+1;
m=1/h+1;
r=ti/h^2; %------------------------------ r为网格比;
w=ones(m,m);
u=ones(m,m); %------------------------输入初始值
v=ones(m,m);
for i=2:m-1
for j=2:m-1
u(i,j)=sin(pi*(i-1)*h)*sin(2*pi*h*(j-1));
end
end
%------------------------输入用P-R差分格式求解的三对角矩阵
b=ones(1,m-2)*(2+2*r);
a=-r*ones(1,m-3);
c=-r*ones(1,m-3);
A=zeros(m-2,m-2); for i=1:m-2
A(i,i)=2-2*r; end
for i=1:m-3 A(i,i+1)=r; A(i+1,i)=r; end
p=zeros(m-2,1); p(1)=2*r; p(m-2)=2*r; tic
for l=1:k
for i=2:m-1
d1=A*u(i,2:m-1)'+p; d1=d1';
w(2:m-1,i)=zg(a,b,c,d1); %-------------------------调用追赶法求解 d2=A*w(2:m-1,i)+p;
v(i,2:m-1)=zg(a,b,c,d2); %-------------------------调用追赶法求解 end u=v'; end toc t=toc u
mesh(0:0.1:1,0:0.1:1,u)
局部一维格式:
11112222
,,1,,1,1,,1,221111
11112222,,,1,,1,1,,122
2211()2222211()222
n n n n n n n n j l j l
j l j l j l j l j l j l n n n n n n n n j l j l j l j l j l j l j l j l u u u u u u u u h h
u u u u u u u u h h
ττ+++++-+-++++
+++++-+-?--+-+?=+?????--+-+?=+??? 将原格式化为:
111
222
1,,1,1,,1,2
111
111222
,1,,1,1,,1
(22)(22),/(22)(22)n n n n n n j l j l j l j l j l j l n n n n n n j l j l j l j l j l j l u u u u u u h u u u u u u λλλλλλλτλλλλλλ++++-+-+++
++++-+-?-++-=+-+?=??-++-=+-+?其中
121,1,1
2
2,2,1
,2,222222222222222222n n
l l n
n l l n m l n m l
u u u u u u λλλλλλ
λ
λλλλλ
λ
λ
λλ
λ
λλλλλ
λλλ
λ
λ+++??
???-+--??
?? ? ? ? ?-+-- ? ? ? ?
? ? ? ?= ? ? ? ? ? ? ? ? ? ?
? ?-+--?????? ? ???
-+-?-+--+-?
1
21,1,1
1
12
,2,211
,2,222222n n j j n n j j n j m n j m
u u u
u u u λλλ
λλλ
λ
λ
λ++++++?
????????????? ????-??? ? ?? ? ?- ? ?? ? ? ? ?? ?
?= ? ?? ? ? ? ?? ? ? ? ? ? ??-??
??? ?? ???
?
代入边界条件,转化为三对角矩阵
122,1,1
2
2,3,1
,21,222222220022222222n n
l l n
n l l n m l n m l
u u u u u u λλλλλ
λλλλλλλ
λ
λλ
λ
λλλλλλ+++-??
???+--??
???? ? ?
? ? ?-+-- ? ? ? ? ?
? ? ? ? ?=+ ? ? ? ? ? ? ? ? ? ?
? ?
? ? ?-+-???????? ? ???
+--+
1
21,1,2
1
12
,3,211
,12,2222002222n n j j n n j j n j m n j m
u u
u
u u u λλλ
λλλλλ
λ
λλ
λ
λλ+++++-+?
????????????
?
????-????
?? ? ??
? ? ?-- ? ?? ? ? ? ? ?? ?
? ?=+ ? ?? ? ? ? ? ? ?
? ? ? ? ? ?
?-+-???
????? ? ???
?
???
附源程序:
%------------------------------------------运用局部一维格式求解二维扩散方程的初边值问题;
function god(ti,hi,t) %------------------------------------------------ti 为时间步长 , hi 为空间步长; m=1/hi;n=t/ti;
g=ti/(hi^2); %--------------------------------- g 为网格比 u=ones(m+1,m+1); %------------------------输入初始值 for i=2:m for j=2:m
u(i,j)=sin(pi*(i-1)*hi)*sin(2*pi*(j-1)*hi); end end
a(1:m-2)=-0.5*g;
b(1:m-1)=1+g;
c(1:m-2)=-0.5*g; %------------------------输入用局部一维差分格式求解的三对角矩阵 B=zeros(m-1,m+1);
for i=1:m-1
B(i,i)=0.5*g;
B(i,i+1)=1-g;
B(i,i+2)=0.5*g;
end
f=zeros(m-1,1);
f(1,1)=0.5*g;
f(m-1,1)=0.5*g;
w=ones(m+1,m+1);
for i=1:n
for j=2:m
d=B*u(:,j)+f;
%-------------------------调用追赶法求解
x=zg(a,b,c,d);
w(2:m,j)=x';
end
for j=2:m
e=B*w(j,:)'+f;
x=zg(a,b,c,e); %-------------------------调用追赶法求解
u(j,2:m)=x;
end
end
u
mesh(u)
古典显式在t=1时运行结果:gdxs(0.0025,0.1,1)
所用时间t=0
1.00000 000000 000 1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000 000000 000 0.99999
999970
799
0.99999
999944
526
0.99999
999923
550
0.99999
999910
241
0.99999
999905
502
0.99999
999910
240
0.99999
999923
550
0.99999
999944
526
0.99999
999970
799
1.00000
000000
000
1.00000 000000 000 0.99999
999944
526
0.99999
999894
348
0.99999
999854
766
0.99999
999829
052
0.99999
999820
481
0.99999
999829
052
0.99999
999854
766
0.99999
999894
348
0.99999
999944
526
1.00000
000000
000
1.00000 000000 000 0.99999
999923
550
0.99999
999854
766
0.99999
999799
851
0.99999
999765
007
0.99999
999752
602
0.99999
999765
007
0.99999
999799
851
0.99999
999854
766
0.99999
999923
550
1.00000
000000
000
1.00000 000000 000 0.99999
999910
240
0.99999
999829
052
0.99999
999765
007
0.99999
999723
401
0.99999
999709
532
0.99999
999723
401
0.99999
999765
007
0.99999
999829
052
0.99999
999910
240
1.00000
000000
000
1.00000 000000 000 0.99999
999905
502
0.99999
999820
481
0.99999
999752
602
0.99999
999709
532
0.99999
999694
199
0.99999
999709
532
0.99999
999752
602
0.99999
999820
481
0.99999
999905
502
1.00000
000000
000
000000 000 999910
240
999829
052
999765
007
999723
401
999709
532
999723
401
999765
007
999829
052
999910
240
000000
000
1.00000 000000 000 0.99999
999923
550
0.99999
999854
766
0.99999
999799
851
0.99999
999765
007
0.99999
999752
602
0.99999
999765
007
0.99999
999799
851
0.99999
999854
766
0.99999
999923
550
1.00000
000000
000
1.00000 000000 000 0.99999
999944
526
0.99999
999894
348
0.99999
999854
766
0.99999
999829
052
0.99999
999820
481
0.99999
999829
052
0.99999
999854
766
0.99999
999894
348
0.99999
999944
526
1.00000
000000
000
1.00000 000000 000 0.99999
999970
799
0.99999
999944
526
0.99999
999923
550
0.99999
999910
240
0.99999
999905
502
0.99999
999910
240
0.99999
999923
550
0.99999
999944
526
0.99999
999970
799
1.00000
000000
000
1.00000 000000 000 1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
P-R 格式t=1时运行结果:pr(0.0025,0.1,1)所用时间t=0.36000000000000
1.00000 000000 000 1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000 000000 000 0.99999
999954
442
0.99999
999913
343
0.99999
999880
727
0.99999
999859
787
0.99999
999852
571
0.99999
999859
787
0.99999
999880
727
0.99999
999913
343
0.99999
999954
442
1.00000
000000
000
1.00000 000000 000 0.99999
999913
343
0.99999
999835
169
0.99999
999773
130
0.99999
999733
298
0.99999
999719
573
0.99999
999733
298
0.99999
999773
130
0.99999
999835
169
0.99999
999913
343
1.00000
000000
000
1.00000 000000 000 0.99999
999880
727
0.99999
999773
130
0.99999
999687
740
0.99999
999632
917
0.99999
999614
026
0.99999
999632
917
0.99999
999687
740
0.99999
999773
130
0.99999
999880
727
1.00000
000000
000
1.00000 000000 000 0.99999
999859
787
0.99999
999733
298
0.99999
999632
917
0.99999
999568
468
0.99999
999546
260
0.99999
999568
468
0.99999
999632
917
0.99999
999733
298
0.99999
999859
787
1.00000
000000
000
1.00000 000000 000 0.99999
999852
571
0.99999
999719
573
0.99999
999614
026
0.99999
999546
260
0.99999
999522
910
0.99999
999546
260
0.99999
999614
026
0.99999
999719
573
0.99999
999852
571
1.00000
000000
000
1.00000 000000 000 0.99999
999859
787
0.99999
999733
298
0.99999
999632
917
0.99999
999568
468
0.99999
999546
260
0.99999
999568
468
0.99999
999632
917
0.99999
999733
298
0.99999
999859
787
1.00000
000000
000
1.00000 000000 000 0.99999
999880
727
0.99999
999773
130
0.99999
999687
740
0.99999
999632
917
0.99999
999614
026
0.99999
999632
917
0.99999
999687
740
0.99999
999773
130
0.99999
999880
727
1.00000
000000
000
1.00000 000000 000 0.99999
999913
343
0.99999
999835
169
0.99999
999773
130
0.99999
999733
298
0.99999
999719
573
0.99999
999733
298
0.99999
999773
130
0.99999
999835
169
0.99999
999913
343
1.00000
000000
000
000000 000 999954
442
999913
343
999880
727
999859
787
999852
571
999859
787
999880
727
999913
343
999954
442
000000
000
1.00000 000000 000 1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
局部一维格式t=1时的运行结果:god(0.0025,0.1,1)所用时间t= 0.39000000000000
1.00000 000000 000 1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000 000000 000 0.99999
999952
157
0.99999
999908
996
0.99999
999874
744
0.99999
999852
753
0.99999
999845
175
0.99999
999852
753
0.99999
999874
744
0.99999
999908
996
0.99999
999952
157
1.00000
000000
000
1.00000 000000 000 0.99999
999908
996
0.99999
999826
901
0.99999
999761
749
0.99999
999719
920
0.99999
999705
506
0.99999
999719
920
0.99999
999761
749
0.99999
999826
901
0.99999
999908
996
1.00000
000000
000
1.00000 000000 000 0.99999
999874
744
0.99999
999761
749
0.99999
999672
076
0.99999
999614
503
0.99999
999594
664
0.99999
999614
503
0.99999
999672
076
0.99999
999761
750
0.99999
999874
744
1.00000
000000
000
1.00000 000000 000 0.99999
999852
753
0.99999
999719
920
0.99999
999614
503
0.99999
999546
821
0.99999
999523
499
0.99999
999546
821
0.99999
999614
503
0.99999
999719
920
0.99999
999852
753
1.00000
000000
000
1.00000 000000 000 0.99999
999845
175
0.99999
999705
506
0.99999
999594
664
0.99999
999523
499
0.99999
999498
977
0.99999
999523
499
0.99999
999594
664
0.99999
999705
506
0.99999
999845
175
1.00000
000000
000
1.00000 000000 000 0.99999
999852
753
0.99999
999719
920
0.99999
999614
503
0.99999
999546
821
0.99999
999523
499
0.99999
999546
821
0.99999
999614
503
0.99999
999719
920
0.99999
999852
753
1.00000
000000
000
1.00000 000000 000 0.99999
999874
744
0.99999
999761
749
0.99999
999672
076
0.99999
999614
503
0.99999
999594
664
0.99999
999614
503
0.99999
999672
076
0.99999
999761
750
0.99999
999874
744
1.00000
000000
000
1.00000 000000 000 0.99999
999908
996
0.99999
999826
901
0.99999
999761
749
0.99999
999719
920
0.99999
999705
506
0.99999
999719
920
0.99999
999761
750
0.99999
999826
901
0.99999
999908
996
1.00000
000000
000
1.00000 000000 000 0.99999
999952
157
0.99999
999908
996
0.99999
999874
744
0.99999
999852
753
0.99999
999845
175
0.99999
999852
753
0.99999
999874
744
0.99999
999908
996
0.99999
999952
157
1.00000
000000
000
1.00000 000000 000 1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
1.00000
000000
000
结论:由上面的表格数据可知:古典显式格式的计算速度最快,且当1/4
λ≤时,才是稳定的,局部一维格式的计算速度最慢,但是它是无条件稳定的,P-R格式的速度居中,也是无条件稳定的。
偏微分方程数值解试题(06B ) 参考答案与评分标准 信息与计算科学专业 一(10分)、设矩阵A 对称,定义)(),(),(2 1)(n R x x b x Ax x J ∈-=,)()(0x x J λλ?+=.若0)0('=?,则称称0x 是)(x J 的驻点(或稳定点).矩阵A 对称(不必正定),求证0x 是)(x J 的驻点的充要条件是:0x 是方程组 b Ax =的解 解: 设n R x ∈0是)(x J 的驻点,对于任意的n R x ∈,令 ),(2),()()()(2 000x Ax x b Ax x J x x J λλλλ?+-+=+=, (3分) 0)0('=?,即对于任意的n R x ∈,0),(0=-x b Ax ,特别取b Ax x -=0,则有0||||),(2000=-=--b Ax b Ax b Ax ,得到b Ax =0. (3分) 反之,若n R x ∈0满足b Ax =0,则对于任意的x ,)(),(2 1)0()1()(00x J x Ax x x J >+==+??,因此0x 是)(x J 的最小值点. (4分) 评分标准:)(λ?的展开式3分, 每问3分,推理逻辑性1分 二(10分)、 对于两点边值问题:?????==∈=+-=0 )(,0)(),()('b u a u b a x f qu dx du p dx d Lu 其中]),([,0]),,([,0)(min )(]),,([0min ],[1b a H f q b a C q p x p x p b a C p b a x ∈≥∈>=≥∈∈ 建立与上述两点边值问题等价的变分问题的两种形式:求泛函极小的Ritz 形式和Galerkin 形式的变分方程。 解: 设}0)(),,(|{11=∈=a u b a H u u H E 为求解函数空间,检验函数空间.取),(1b a H v E ∈,乘方程两端,积分应用分部积分得到 (3分) )().(),(v f fvdx dx quv dx dv dx du p v u a b a b a ==+=??,),(1 b a H v E ∈? 即变分问题的Galerkin 形式. (3分)
一.填空(1553=?分) 1.若步长趋于零时,差分方程的截断误差0→lm R ,则差分方程的解lm U 趋近于微分方 程的解lm u . 此结论_______(错或对); 2.一阶Sobolev 空间{} )(,,),()(21 Ω∈''=ΩL f f f y x f H y x 关于内积=1),( g f _____________________是Hilbert 空间; 3.对非线性(变系数)差分格式,常用 _______系数法讨论差分格式的_______稳定性; 4.写出3 x y =在区间]2,1[上的两个一阶广义导数:_________________________________, ________________________________________; 5.隐式差分格式关于初值是无条件稳定的. 此结论_______(错或对)。 二.(13分)设有椭圆型方程边值问题 用1.0=h 作正方形网格剖分 。 (1)用五点菱形差分格式将微分方程在内点离散化; (2)用截断误差为)(2 h O 的差分法将第三边界条件离散化; (3)整理后的差分方程组为 三.(12)给定初值问题 x u t u ??=?? , ()10,+=x x u 取时间步长1.0=τ,空间步长2.0=h 。试合理选用一阶偏心差分格式(最简显格式), 并以此格式求出解函数),(t x u 在2.0,2.0=-=t x 处的近似值。 1.所选用的差分格式是: 2.计算所求近似值: 四.(12分)试讨论差分方程 ()h a h a r u u r u u k l k l k l k l ττ + - = -+=++++11,111 1 逼近微分方程 0=??+??x u a t u 的截断误差阶R 。 思路一:将r 带入到原式,展开后可得格式是在点(l+1/2,k+1/2)展开的。 思路二:差分格式的用到的四个点刚好是矩形区域的四个顶点,可由此构造中心点的差分格 式。
偏微分方程数值解 偏微分方程地构建科学、工程学和其他领域的数学模型的主要手段。一般情况下,这些模型都需要用数值方法去求解。本书提供了标准数值技术的简明介绍。借助抛物线型、双曲线型和椭圆型方程的一些简单例子介绍了常用的有限差分方法、有限元方法、有限体方法、修正方程分析、辛积分格式、对流扩散问题、多重网络、共轭梯度法。利用极大值原理、能量法和离散傅里叶分析清晰严格地处理了稳定性问题。本书全面讨论了这些方法的性质,并附有典型的图像结果,提供了不同难度的例子和练习。 本书可作为数学、工程学及计算机科学专业本科教材,也可供工程技术人员和应用工作者参考。 偏微分方程数值解---学习总结(2) 关于SobolveSobolve空间的几个重要定理 迹定理 : ΩΩ是 RdRd 的一个有界开子集,具有李普希茨连续边界?Ω?Ω, s>12s>12, 则 a.存在唯一的连续线性映射γ0:Hs(Ω)→Hs?12(?Ω),满足γ0v=v ∣∣?Ω,?v∈Hs(Ω)∩C0(Ωˉˉˉˉ), b.存在唯一的连续映射R0:Hs?12(?Ω)→Hs(Ω),满足γ0°R0°φ=φ,?φ∈Hs?12(?Ω).(1)(2)(1)a.存在唯一的连续线性映射γ0:Hs(Ω)→Hs?12(?Ω),满足γ0v=v|?Ω,?v∈
Hs(Ω)∩C0(Ωˉ),(2)b.存在唯一的连续映射R0:Hs?12(?Ω)→Hs(Ω),满足γ0°R0°φ=φ,?φ∈Hs?12(?Ω). 迹定理把区域内部与边界联系起来. 上面定理中边界?Ω?Ω当被它的一个子集ΣΣ代替时,结论依然成立. S=1时, γ0:H1(Ω)→H12(?Ω)?L2(?Ω)||γ0v||0,?Ω≤||γ0v||2,?Ω≤C||v||1=C(||v||0+||?v||0).γ0:H1(Ω)→H12(?Ω)? L2(?Ω)||γ0v||0,?Ω≤||γ0v||2,?Ω≤C||v||1=C(||v||0+||? v||0). 注意几个范数 ||?||k||?||0||?||1||??||0=||?||k,2=||?||L2=||?||1,2=(||?||20+||??||20)12=|?|1.(3)(4)(5)(6)(3)||?||k=||?||k,2(4)||? ||0=||?||L2(5)||?||1=||?||1,2=(||?||02+||??||02)12(6)||?? ||0=|?|1. 庞加莱不等式(Poincare inequality): 假设ΩΩ是 RdRd 的一个有界联通开子集,ΣΣ是边界?Ω?Ω的一个非空的李普希茨连续子集. 则存在一个常数 CΩ>0CΩ>0满足 ∫Ωv2(x)dx≤CΩ∫Ω|?v(x)|2dx,?v∈H1Σ(Ω),其中H1Σ(Ω)={v ∈H1(Ω),γΣv=v∣∣Σ=0}.∫Ωv2(x)dx≤CΩ∫Ω|?v(x)|2dx,?v∈HΣ1(Ω),其中HΣ1(Ω)={v∈H1(Ω),γΣv=v|Σ=0}.
偏微分方程数值解试题(06B) 参考答案与评分标准 信息与计算科学专业 一(10分)、设矩阵A 对称,定义)(),(),(2 1 )(n R x x b x Ax x J ∈-= ,)()(0x x J λλ?+=.若0)0('=?,则称称0x 是)(x J 的驻点(或稳定点).矩阵A 对称(不必正定),求证0x 是)(x J 的驻点的充要条件是:0x 是方程组 b Ax =的解 解: 设n R x ∈0是)(x J 的驻点,对于任意的n R x ∈,令 ),(2 ),()()()(2 000x Ax x b Ax x J x x J λλλλ?+ -+=+=, (3分) 0)0('=?,即对于任意的n R x ∈,0),(0=-x b Ax ,特别取b Ax x -=0,则有 0||||),(2000=-=--b Ax b Ax b Ax ,得到b Ax =0. (3分) 反之,若 n R x ∈0满足 b Ax =0,则对于任意的 x ,)(),(2 1 )0()1()(00x J x Ax x x J >+ ==+??,因此0x 是)(x J 的最小值点. (4分) 评分标准:)(λ?的展开式3分, 每问3分,推理逻辑性1分 二(10分)、 对于两点边值问题:????? ==∈=+-=0 )(,0)() ,()(' b u a u b a x f qu dx du p dx d Lu 其中]),([,0]),,([,0)(min )(]),,([0min ] ,[1b a H f q b a C q p x p x p b a C p b a x ∈≥∈>=≥∈∈ 建立与上述两点边值问题等价的变分问题的两种形式:求泛函极小的Ritz 形式和 Galerkin 形式的变分方程。 解: 设}0)(),,(|{11 =∈=a u b a H u u H E 为求解函数空间,检验函数空间.取),(1 b a H v E ∈,乘方程两端,积分应用分部积分得到 (3分) )().(),(v f fvdx dx quv dx dv dx du p v u a b a b a ==+=??,),(1 b a H v E ∈? 即变分问题的Galerkin 形式. (3分) 令?-+=-=b a dx fu qu dx du p u f u u a u J ])([21),(),(21)(22,则变分问题的Ritz 形式
偏微分方程数值解实验报告
1、用有限元方法求下列边值问题的数值解:''()112x -y +y =2s i n ,0
1、 %Ritz Galerkin方法求解方程 function u1=Ritz(x) %定义步长 h=1/100; x=0:h:1; n=1/h; a=zeros(n-1,1); b=zeros(n,1); c=zeros(n-1,1); d=zeros(n,1); %求解Ritz方法中内点系数矩阵 for i=1:1:n-1 b(i)=(1/h+h*pi*pi/12)*2; d(i)=h*pi*pi/2*sin(pi/2*(x(i)+h))/2+h*pi*pi/2*sin(pi/2*x(i+1))/2; end %右侧导数条件边界点的计算 b(n)=(1/h+h*pi*pi/12); d(n)=h*pi*pi/2*sin(pi/2*(x(i)+h))/2; for i=1:1:n-1 a(i)=-1/h+h*pi*pi/24; c(i)=-1/h+h*pi*pi/24; end %调用追赶法 u=yy(a,b,c,d) %得到数值解向量 u1=[0,u] %对分段区间做图 plot(x,u1) %得到解析解 y1=sin(pi/2*x); hold on plot(x,y1,'o') legend('数值解','解析解') function x=yy(a,b,c,d) n=length(b); q=zeros(n,1); p=zeros(n,1); q(1)=b(1); p(1)=d(1); for i=2:1:n
偏微分方程数值解期末复习(2011硕士) 一、考题类型 本次试卷共六道题目,题型及其所占比例分别为: 填空题20%;计算题80% 二、按章节复习内容 第一章 知识点:Euler法、向前差商、向后差商、中心差商、局部截断误差、整体截断误差、相容性、收敛性、阶、稳定性、显格式、隐格式、线性多步法、第一特征多项式、第二特征多项式、稳定多项式、绝对稳定等; 要求: 会辨认差分格式, 判断线性多步法的误差和阶; 第二章 知识点:矩形网格、(正则,非正则)内点、边界点、偏向前(向后,中心)差商、五点差分格式、增设虚点法、积分插值法、线性椭圆型差分格式、极值原理、比较定理、五点差分格式的相容收敛和、稳定性等; 要求: 建立椭圆型方程边值问题的差分格式, 极值原理; 第四章 知识点:最简显格式、最简隐格式、CN格式、双层加权格式、Richardson 格式、网格比、传播因子法(分离变量法) 、传播因子、传播矩阵、谱半径、von Neumann条件、跳点格式、ADI格式、线性椭圆型差分格式、极值原理、比较定理、五点差分格式的相容收敛和稳定性等; 要求: 建立抛物型方程边值问题的差分格式, 计算局部截断误差; 第五章 知识点:左偏心格式、右偏心格式、中心格式、LF格式、LW格式、Wendroff 格式、跳蛙格式、特征线、CFL条件等; 要求: 建立双曲型方程边值问题的差分格式, 计算局部截断误差; 第七章 要求: 会用线性元(线性基)建立常微分方程边值问题的有限元格式
三 练习题 1、 已知显格式21131()22 n n n n u u h f f +++-=-,试证明格式是相容的,并求它的阶。 P39+P41 2、用Taylor 展开原理构造一元函数一阶导数和二阶导数的数值微分公式。 提示:向前、向后和中心差商与一阶导数间关系,二阶中心差商与二阶导数 之间的关系 课件 3、用数值微分方法或数值积分方法建立椭圆型方程 2222(,),(,),u u f x y x y x y ??--=?∈Ω?? :01,01x y Ω≤≤≤≤ 内点差分格式。 P75+课件 4、构造椭圆型方程边值问题的差分格式. P101 (4)题 5、构建一维热传导方程220,(0)u u Lu a a t x ??=-=>??的数值差分格式(显隐格式等)。 参考P132-135相关知识点 6、设有逼近热传导方程22(0)u u Lu a f a const t x ??≡-==>??的带权双层格式 ()()1111111122(1)2k k j j k k k k k k j j j j j j u u a u u u u u u h θθτ++++-+-+-??=-++--+?? 其中[0,1]θ∈,试求其截断误差。并证明当2 1212h a θτ=-时,截断误差的阶最 高阶为24()O h τ+。 P135+P165+课件 7、传播因子法证明抛物型方程22(0)u u Lu a f a const t x ??≡-==>??的最简显隐和六点CN 格式稳定性。 P156+课件 8、对一阶常系数双曲型方程的初边值问题 0,0,0,0,(,0)(),0,(0,)(),0, u u a t T x a t x u x x x u t t t T φψ???+=<≤<<∞>?????=≤<∞??=≤≤?
专业班级 姓名 学号 开课系室数学与计算科学学院 考试日期
偏微分方程数值解试卷 一(15分)、(1)简述用差分方法求解抛物型方程初边值问题的数值解的一般步骤.(2)写出近似一阶偏导数 n m x u |??的三种有限差分逼近及其误差阶,写出近似 n m x u |22 ??的差分逼近及其误差阶. 评分标准: (1) 7分,三个离散4分,其他步骤3分 (2) 8分,每个格式及误差2分。 二(15分)、(1)以抛物型方程的差分格式为例,解释差分格式的相容性,稳定性和收敛性概念,分析相容性,稳定性和收敛性与误差的关系,简述 Lax 等价性定理。(2) 简述差分格式稳定性分析的Fourier 级数法(或称为Neumann Von 方法,分离变量法)的一般步骤。 (1)8分,解释概念6分,等价关系2分 (2)7分,典型波2分,放大因子与条件3分,其他2分 三(20分)、对于边值问题 ?? ???=?=∈=??+???0 |) 1,0()1,0(),(,92 222G u G y x y u x u (1)建立该边值问题的五点差分格式(五点棱形格式又称正五点格式),推导截 断误差的阶。 (2)取3/1=h ,求边值问题的数值解(写出对应的方程组的矩阵形式并求解) (3)就取5/1=h 的情况写出对应方程组的系数矩阵(用分块矩阵表示)。 解:(1)7分,离过程与格式
第二页(共五页) 四(20分)、对于初边值问题??? ????≤≤==<<=≤<<
课程设计报告 课程:偏微分方程数值解学号: 姓名: 班级: 教师:
《偏微分方程数值解》 课程设计指导书 一.课程设计的目的 1.帮助掌握偏微分方程数值解相关知识。 2.理解偏微分方程数值解差分隐格式解决自由振动方程问题的方法。 3.锻炼编写程序代码的能力。 二.设计名称 差分法求自由振动问题的周期解。 三.设计要求 1.要求写出差分隐格式的理论方法。 2.要求编写matlab 程序,画出函数图形。 3.要求写出实验总结及心得体会。 四.设计题目 用差分法求自由振动问题的周期解: 2222000,,0|0,|sin (0,)(2,)t t u u x t t x u u x t u t u t π==???-=-∞<<∞>???? ??==??? =??? 要求用差分隐格式求解,其中14 θ= 。 五.设计细则 1.区域剖分: 构造上式的差分逼近,取空间步长h 和时间步长τ,用两族平行直线 ?? ?===±±=== ,2,1,0,, ,2,1,0,n n t t j jh x x n j τ 作矩形网格。 2.离散格式: 显格式: 于网点),(n j t x 用Taylor 展式,并整理方程得: ??? ?? ??--++=+-++==-+-++-121121102 10102100 )1(2)(),()()1()]()([2),(n j n j n j n j n j j j j j j j j u u r u u r u x x r x x r u x u τ?????
隐格式: 上述显格式并不是绝对稳定的差分格式,为了得到绝对稳定的差分格式,用第1-n 层、 n 层、1+n 层的中心差商的权平均去逼近xx u ,得到下列差分格式: ? ??? ?? ???+-++--++-=+-+-++==----+-++-+++-++-]22)21(2[2), ()()1()]()([2),(2111112112111112 211102 10102100h u u u h u u u h u u u a u u u x x r x x r u x u n j n j n j n j n j n j n j n j n j n j n j n j j j j j j j j θθθττ?????其中10≤≤θ是参数。当0=θ时就是显格式,而当4 1 =θ时可以证明该格式绝对稳定。 隐格式的矩阵形式是: ??? ???????? ???????????=??????????????????????????????????????????????? ?-+-+-+-+--+-+-+++122111121121 12222 222 2222221212121J J j n J n J n j n n z z z z z u u u u u r r r r r r r r r r r r θθθθ θθθθθ θ θθ 其中: 1 111111122]2()2)(21[(-----+-+-++-++--=n j n j n j n j n j n j n j n j j u u u u u u u u r z θθ 3.格式稳定性: 1)显格式: 显格式稳定的充分必要条件是:网格比1 引言 偏微分方程定解问题有着广泛的应用背景。人们用偏微分方程来描述、解释或者预见各种自然现象,并用于科学和工程技术的各个领域fll。然而,对于广大应用工作者来说,从偏微分方程模型出发,使用有限元法或有限差分法求解都要耗费很大的工作量,才能得到数值解。现在,MATLAB PDEToolbox已实现对于空间二维问题高速、准确的求解过程。 偏微分方程 如果一个微分方程中出现的未知函数只含一个自变量,这个方程叫做常微分方程,也简称微分方程;如果一个微分方程中出现多元函数的偏导数,或者说如果未知函数和几个变量有关,而且方程中出现未知函数对几个变量的导数,那么这种微分方程就是偏微分方程。 常用的方法有变分法和有限差分法。变分法是把定解问题转化成变分问题,再求变分问题的近似解;有限差分法是把定解问题转化成代数方程,然后用计算机进行计算;还有一种更有意义的模拟法,它用另一个物理的问题实验研究来代替所研究某个物理问题的定解。虽然物理现象本质不同,但是抽象地表示在数学上是同一个定解问题,如研究某个不规则形状的物体里的稳定温度分布问题,由于求解比较困难,可作相应的静电场或稳恒电流场实验研究,测定场中各处的电势,从而也解决了所研究的稳定温度场中的温度分布问题。 随着物理科学所研究的现象在广度和深度两方面的扩展,偏微分方程的应用范围更广泛。从数学自身的角度看,偏微分方程的求解促使数学在函数论、变分法、级数展开、常微分方程、代数、微分几何等各方面进行发展。从这个角度说,偏微分方程变成了数学的中心。 一、MATLAB方法简介及应用 1.1 MATLAB简介 MATLAB是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。 1.2 Matlab主要功能 数值分析 数值和符号计算 工程与科学绘图 控制系统的设计与仿真 数字图像处理 数字信号处理 通讯系统设计与仿真 财务与金融工程 1.3 优势特点 1) 高效的数值计算及符号计算功能,能使用户从繁杂的数学运算分析中解脱出来; 2) 具有完备的图形处理功能,实现计算结果和编程的可视化; 3) 友好的用户界面及接近数学表达式的自然化语言,使学者易于学习和掌握; 4) 功能丰富的应用工具箱(如信号处理工具箱、通信工具箱等) , 偏微分方程数值解试题 1、考虑一维的抛物型方程: 2200, [0,], 0t T (,), (,)(,0)() x x u u x t x u x t u u x t u u x x ππνπ?==??=∈≤≤??=== (1)导出时间离散是一阶向前Euler 格式,空间离散是二阶精度的差分格式; (2)讨论(1)中导出的格式的稳定性; (3)若时间离散为二阶精度的蛙跳格式, 11 2n n n t t u u u t t +-=?-= ?? 空间离散是二阶精度的中心差分,问所导出的格式稳定吗?为什么? 2、考虑Poission 方程 2(,)1, (,)0, in AB and AD (,)0, in BC and CD u x y x y u n u x y -?=∈Ω ?=?= 其中Ω是图1中的梯形。 使用差分方法来离散该方程。由于梯形的对称性,可以考虑梯形的一半,如图2, 图2 从物理空间到计算区域的几何变换 图1 梯形 为了求解本问题,采用如下方法:将Ω的一半投影到正方形区域?Ω ,然后在?Ω上使用差分方法来离散该方程。在计算区域?Ω 上用N N ?个网格点,空间步长为1/(1)N ξη?=?=-。 (1)引入一个映射T 将原区域Ω(带有坐标,x y )变换到单位正方形?Ω(带有坐标,ξη)。 同时导出在新区域上的方程和边界条件。 (2)在变换区域,使用泰勒展开导出各导数项在区域内部和边界点上的差分格式。 3、对线性对流方程0 constant >0u u a a t x ??+=??,其一阶迎风有限体积法离散格式为 1?n j u +=?n j u a t x ?-?(?n j u 1?n j u --) (1)写出0a <时的一阶迎风有限体积法的离散格式; (2)写出a 为任意符号的常数的一阶迎风有限体积法的守恒形式。 (3)使用0 u u u t x ??+=??说明一阶迎风有限体积法不是熵保持的格式。 4、对一维Poission 方程 , (0,1) (0)(1)0 x xx u xe x u u ?-=∈? ==? 将[]01,分成(1)n +等分,写出用中心差分离散上述方程的差分格式,并问: (1)该差分格式与原微分方程相容吗?为什么? (2)该差分格式稳定吗?为什么? (3)该差分格式是否收敛到原微分方程的解?为什么? (4)取(1)6n +=,写出该差分格式的矩阵表示。 5、叙述二重网格方法的执行过程,并对一维常微分方程边值问题 2 25, (0,1) (0)(1)0 xx u x x x u u πππ?-=∈? ==?(sin(5)+9sin(15)) 给出限制算子和延拓算子矩阵(以细网格h :7n =,粗网格2h :3n =为例)。 6、对一阶波动方程 01(,0)sin(), (0,1)2(0,)(1,)u u t x u x x x u t u t π???+=???? ? =∈?? =??? (1)写出用中心差分进行空间离散,用一阶向后Euler 进行时间离散的差分格式; 精品文档 偏微分方程数值解 上 机 实 验 报 告 (一)实验一 一、上机题目: 用线性元求解下列边值问题的数值解: 精品文档 ′′22?? ?? ??,0 精品文档 (二)实验二 四、上机题目: 求解 Helmholtz 方程的边值问题: u k 2u 1 ,于(0,1)*(0,1) u0,于1{ x0,0y1} U{0x1, y 1} 1{ x0,0y1} U{0x1, y1} u 0,于2{0x1, y 0} U { x1,0y1} n 其中 k=1,5,10,15,20 五、实验程序: 1 / 7 偏微分方程数值解试题 1、考虑一维的抛物型方程: 2200, [0, ], 0t T (,), (,)(,0)() x x u u x t x u x t u u x t u u x x ππνπ?==??=∈≤≤??=== (1)导出时间离散是一阶向前Euler 格式,空间离散是二阶精度的差分格式; (2)讨论(1)中导出的格式的稳定性; (3)若时间离散为二阶精度的蛙跳格式, 11 2n n n t t u u u t t +-=?-=?? 空间离散是二阶精度的中心差分,问所导出的格式稳定吗?为什么? 2、考虑Poission 方程 2(,)1, (,)0, in AB and AD (,)0, in BC and CD u x y x y u n u x y -?=∈Ω ?=?= 其中Ω是图1中的梯形。 使用差分方法来离散该方程。由于梯形的对称性,可以考虑梯形的一半,如图2, 图2 从物理空间到计算区域的几何变换 图1 梯形 2 / 7 为了求解本问题,采用如下方法:将Ω的一半投影到正方形区域?Ω ,然后在?Ω上使用差分方法来离散该方程。在计算区域?Ω 上用N N ?个网格点,空间步长为1/(1)N ξη?=?=-。 (1)引入一个映射T 将原区域Ω(带有坐标,x y )变换到单位正方形?Ω(带有坐标,ξη)。 同时导出在新区域上的方程和边界条件。 (2)在变换区域,使用泰勒展开导出各导数项在区域内部和边界点上的差分格式。 3、对线性对流方程 0 constant >0u u a a t x ??+=??,其一阶迎风有限体积法离散格式为 1?n j u +=?n j u a t x ?-?(?n j u 1?n j u --) (1)写出0a <时的一阶迎风有限体积法的离散格式; (2)写出a 为任意符号的常数的一阶迎风有限体积法的守恒形式。 (3)使用0 u u u t x ??+=??说明一阶迎风有限体积法不是熵保持的格式。 4、对一维Poission 方程 , (0,1)(0)(1)0 x xx u xe x u u ?-=∈?==? 将[]01,分成(1)n +等分,写出用中心差分离散上述方程的差分格式,并问: (1)该差分格式与原微分方程相容吗?为什么? (2)该差分格式稳定吗?为什么? (3)该差分格式是否收敛到原微分方程的解?为什么? (4)取(1)6n +=,写出该差分格式的矩阵表示。 5、叙述二重网格方法的执行过程,并对一维常微分方程边值问题 225, (0,1)(0)(1)0 xx u x x x u u πππ?-=∈?==?(sin(5)+9sin(15)) 给出限制算子和延拓算子矩阵(以细网格h :7n =,粗网格2h :3n =为例)。 6、对一阶波动方程 1(,0)sin(), (0,1)2(0,)(1,)u u t x u x x x u t u t π???+=?????=∈??=??? (1)写出用中心差分进行空间离散,用一阶向后Euler 进行时间离散的差分格式; 一、 问题 用有限元方法求下面方程的数值解 2 u u u f t ?-?+=? in (]0,T Ω? 0u = on []0,T ?Ω? ()00,u x u = in Ω 二、 问题分析 第一步 利用Green 公式,求出方程的变分形式 变分形式为:求()()21 00,;u L T H ∈Ω,使得 ()())(2 ,,,,u v u v u v f v t ???+??+= ???? ()10v H ?∈Ω (*) 以及 ()00,u x u =. 第二步 对空间进行离散,得出半离散格式 对区域Ω进行剖分,构造节点基函数,得出有限元子空间:()12,,,h NG V span ???=???,则(*)的Galerkin 逼近为: []0,t T ?∈,求()()1 0,h h u t x V H ∈?Ω,使得 ()()()()() () )(2 ,,,,h h h h h h h d u t v u t v u t v f v dt +??+= h h v V ?∈ (**) 以及()0,0h h u u =,0,h u 为初始条件0u 在h V 中的逼近,设0,h u 为0u 在h V 中的插值. 则0t ?≥,有()()1 N G h i i i u t t ξ? == ∑,0,h u =01 N G i i i ξ?=∑,代人(**)即可得到一常微分方程组. 第三步 进一步对时间进行离散,得到全离散的逼近格式 对 du dt 用差分格式.为此把[]0,T 等分为n 个小区间[]1,i i t t -,其长度1i i T t t t n -?=-= ,n t T =. 这样把求i t 时刻的近似记为i h u ,0 h u 是0u 的近似.这里对(**)采用向后的欧拉格式,即 ()()() () )(2 11 11 1 ,,,,i i i i h h h h h h h i h u u v u v u v f v t ++++-+??+ = ? h h v V ?∈ (***) i=0,1,2…,n-1. 0 h u =0,h u 由于向后欧拉格式为隐式格式且含有非线性项,故相邻两时间步之间采用牛顿迭代,即: 偏微分方程数值解 一(10分)、设矩阵A 对称正定,定义)(),(),(2 1 )(n R x x b x Ax x J ∈-= ,证明下列两个问题等价:(1)求n R x ∈0使)(min )(0x J x J n R x ∈=;(2)求下列方程组的解:b Ax = 解: 设n R x ∈0是)(x J 的最小值点,对于任意的n R x ∈,令 ),(2 ),()()()(2 000x Ax x b Ax x J x x J λλλλ?+ -+=+=, (3分) 因此0=λ是)(λ?的极小值点,0)0('=?,即对于任意的n R x ∈,0),(0=-x b Ax ,特别取b Ax x -=0,则有0||||),(2000=-=--b Ax b Ax b Ax ,得到b Ax =0. (3分) 反之,若 n R x ∈0满足 b Ax =0,则对于任意的x , )(),(2 1 )0()1()(00x J x Ax x x J >+ ==+??,因此0x 是)(x J 的最小值点. (4分) 评分标准:)(λ?的表示式3分, 每问3分,推理逻辑性1分 二(10分)、对于两点边值问题:????? ==∈=+-=0 )(,0)() ,()(b u a u b a x f qu dx du p dx d Lu 其中]),([,0]),,([,0)(min )(]),,([0min ] ,[1b a H f q b a C q p x p x p b a C p b a x ∈≥∈>=≥∈∈ 建立与上述两点边值问题等价的变分问题的两种形式:求泛函极小的Ritz 形式和 Galerkin 形式的变分方程。 解: 设}0)()(),,(|{11 0==∈=b u a u b a H u u H 为求解函数空间,检验函数空间.取),(10b a H v ∈,乘方程两端,积分应用分部积分得到 (3分) )().(),(v f fvdx dx quv dx dv dx du p v u a b a b a ==+=??,),(10 b a H v ∈? 即变分问题的Galerkin 形式. (3分) 二、改进的Euler 方法 梯形方法的迭代公式(1.10)比Euler 方法精度高,但其计算较复杂,在应用公式(1.10)进行计算时,每迭代一次,都要重新计算函数),(y x f 的值,且还要判断何时可以终止或转下一步计算.为了控制计算量和简化计算法,通常只迭代一次就转入下一步计算.具体地说,我们先用Euler 公式求得一个初步的近似值1+n y ,称之为预测值,然后用公式(1.10)作一次迭代得1+n y ,即将1+n y 校正一次.这样建立的预测-校正方法称为改进的Euler 方法: 预测: ),,(1n n n n y x hf y y +=+ 校正 : )].,(),([2 111+++++=n n n n n n y x f y x f h y y (1.15) 这个计算公式也可以表示为 11(,), (,), 1(). 2p n n n c n n p n p c y y hf x y y y hf x y y y y ++?=+??=+?? ?=+??? 例1 取步长0.1h =,分别用Euler 方法及改进的Euler 方法求解初值问题 d (1),01, d (0) 1. y y xy x x y ?=-+≤≤???=? 解 这个初值问题的准确解为()1(21)x y x e x =--. 根据题设知 ).1(),(xy y y x f +-= (1) Euler 方法的计算式为 )],1([1.01n n n n n y x y y y +?-=+ 由1)0(0==y y , 得 ,9.0)]101(1[1.011=?+??-=y ,8019.0)]9.01.01(9.0[1.09.02=?+??-=y 这样继续计算下去,其结果列于表9.1. (2) 改进的Euler 方法的计算式为 110.1[(1)],0.1[(1)], 1(), 2p n n n n c n p n p n p c y y y x y y y y x y y y y ++?=-?+?=-?+??? ?=+??? 由1)0(0==y y ,得 x ∈R n 2 ( Ax, x) , J ( x + x) = ? (1) = ? (0) + ( Ax, x) > J ( x ) ,因此 x 是 J ( x ) 的最小值点. (4 分) 2 二(10 分)、对于两点边值问题: ? dx dx a(u , v) = ?b ( p . + q u v)dx = ?b fvdx = f (v) , ? v ∈ H 1 (a , b ) dx dx a a 偏微分方程数值解 一(10 分)、设矩阵 A 对称正定,定义 J ( x ) = 1 ( Ax , x ) - (b , x ) ( x ∈ R n ) ,证明下 2 列两个问题等价:(1)求 x ∈ R n 使 J ( x ) = min J ( x ) ;(2)求下列方程组的解:Ax = b 解: 设 x ∈ R n 是 J ( x ) 的最小值点,对于任意的 x ∈ R n ,令 ?(λ) = J ( x + λx) = J ( x ) + λ( Ax - b , x) + λ2 (3 分) 因此 λ = 0 是 ?(λ) 的极小值点 , ? ' (0) = 0 ,即对于任意的 x ∈ R n , ( Ax - b , x) = 0 ,特 0 别取 x = Ax - b ,则有 ( Ax - b , Ax - b ) =|| Ax - b || 2 = 0 ,得到 Ax = b . (3 分) 0 0 反 之 , 若 x ∈ R n 满 足 Ax = b , 则 对 于 任 意 的 x , 1 0 0 0 评分标准: ?(λ) 的表示式 3 分, 每问 3 分,推理逻辑性 1 分 ? d du ?Lu = - ( p ) + qu = f x ∈ (a, b ) ?? u (a) = 0, u (b ) = 0 其中 p ∈ C 1 ([a , b ]), p ( x ) ≥ min p ( x ) = p x ∈[a,b ] min > 0, q ∈ C ([a , b ]), q ≥ 0, f ∈ H 0 ([a , b ]) 建立与上述两点边值问题等价的变分问题的两种形式:求泛函极小的 Ritz 形式和 Galerkin 形式的变分方程。 解 : 设 H 1 = {u | u ∈ H 1 (a , b ), u (a ) = u (b ) = 0} 为求解函数空间 , 检验函数空间 . 取 v ∈ H 1 (a, b ) ,乘方程两端,积分应用分部积分得到 (3 分) du dv 即变分问题的 Galerkin 形式. (3 分) 第十章 偏微分方程数值解法 偏微分方程问题,其求解十分困难。除少数特殊情况外,绝 大多数情况均难以求出精确解。因此,近似解法就显得更为重要。本章仅介绍求解各类典型偏微分方程定解问题的差分方法。 §1 差分方法的基本概念 1.1 几类偏微分方程的定解问题 椭圆型方程:其最典型、最简单的形式是泊松(Poisson )方程 ),(22 2 2y x f y u x u u =??+??=? 特别地,当 0),(≡y x f 时,即为拉普拉斯(Laplace )方程,又称 为调和方程 22 22 =??+??=?y u x u u Poisson 方程的第一边值问题为 ?? ?? ?Ω ?=Γ=Ω∈=??+??Γ∈),(),(),(),(),(22 22y x y x u y x y x f y u x u y x ? 其中 Ω为以Γ为边界的有界区域,Γ为分段光滑曲线, ΓΩY 称为定解区域,),(y x f ,),(y x ?分别为Ω,Γ上的已知连 续函数。 第二类和第三类边界条件可统一表示为 ),(),(y x u u y x ?α=??? ? ??+??Γ∈n 其中n 为边界Γ的外法线方向。当0=α时为第二类边界条件, 0≠α时为第三类边界条件。 抛物型方程:其最简单的形式为一维热传导方程 2 20(0)u u a a t x ??-=>?? 方程可以有两种不同类型的定解问题: 初值问题 ?? ???+∞ <<∞-=+∞<<-∞>=??-??x x x u x t x u a t u )()0,(,00 22 ? 初边值问题 2 212 00,0(,0)()0(0,)(),(,)()0u u a t T x l t x u x x x l u t g t u l t g t t T ????-=<<<
(完整版)偏微分方程的MATLAB解法
偏微分方程数值解(试题)
偏微分方程数值解实验报告
偏微分方程数值解(试题)
偏微分方程数值解法
偏微分方程数值解试题参考答案
偏微分方程数值解例题答案
偏微分方程数值解试题参考答案
第十章-偏微分方程数值解法