
Reprinted with corrections from The Bell System Technical Journal,
V ol.27,pp.379–423,623–656,July,October,1948.
A Mathematical Theory of Communication
By C.E.SHANNON
I NTRODUCTION
HE recent development of various methods of modulation such as PCM and PPM which exchange
bandwidth for signal-to-noise ratio has intensi?ed the interest in a general theory of communication.A basis for such a theory is contained in the important papers of Nyquist1and Hartley2on this subject.In the present paper we will extend the theory to include a number of new factors,in particular the effect of noise in the channel,and the savings possible due to the statistical structure of the original message and due to the nature of the?nal destination of the information.
The fundamental problem of communication is that of reproducing at one point either exactly or ap-proximately a message selected at another point.Frequently the messages have meaning;that is they refer to or are correlated according to some system with certain physical or conceptual entities.These semantic aspects of communication are irrelevant to the engineering problem.The signi?cant aspect is that the actual message is one selected from a set of possible messages.The system must be designed to operate for each possible selection,not just the one which will actually be chosen since this is unknown at the time of design.
If the number of messages in the set is?nite then this number or any monotonic function of this number can be regarded as a measure of the information produced when one message is chosen from the set,all choices being equally likely.As was pointed out by Hartley the most natural choice is the logarithmic function.Although this de?nition must be generalized considerably when we consider the in?uence of the statistics of the message and when we have a continuous range of messages,we will in all cases use an essentially logarithmic measure.
The logarithmic measure is more convenient for various reasons:
1.It is practically more useful.Parameters of engineering importance such as time,bandwidth,number
of relays,etc.,tend to vary linearly with the logarithm of the number of possibilities.For example,
adding one relay to a group doubles the number of possible states of the relays.It adds1to the base2
logarithm of this number.Doubling the time roughly squares the number of possible messages,or
doubles the logarithm,etc.
2.It is nearer to our intuitive feeling as to the proper measure.This is closely related to(1)since we in-
tuitively measures entities by linear comparison with common standards.One feels,for example,that
two punched cards should have twice the capacity of one for information storage,and two identical
channels twice the capacity of one for transmitting information.
3.It is mathematically more suitable.Many of the limiting operations are simple in terms of the loga-
rithm but would require clumsy restatement in terms of the number of possibilities.
The choice of a logarithmic base corresponds to the choice of a unit for measuring information.If the base2is used the resulting units may be called binary digits,or more brie?y bits,a word suggested by J.W.Tukey.A device with two stable positions,such as a relay or a?ip-?op circuit,can store one bit of information.N such devices can store N bits,since the total number of possible states is2N and log22N N.
If the base10is used the units may be called decimal digits.Since
log2M log10M log102
332log10M
1Nyquist,H.,“Certain Factors Affecting Telegraph Speed,”Bell System Technical Journal,April1924,p.324;“Certain Topics in Telegraph Transmission Theory,”A.I.E.E.Trans.,v.47,April1928,p.617.
2Hartley,R.V.L.,“Transmission of Information,”Bell System Technical Journal,July1928,p.535.
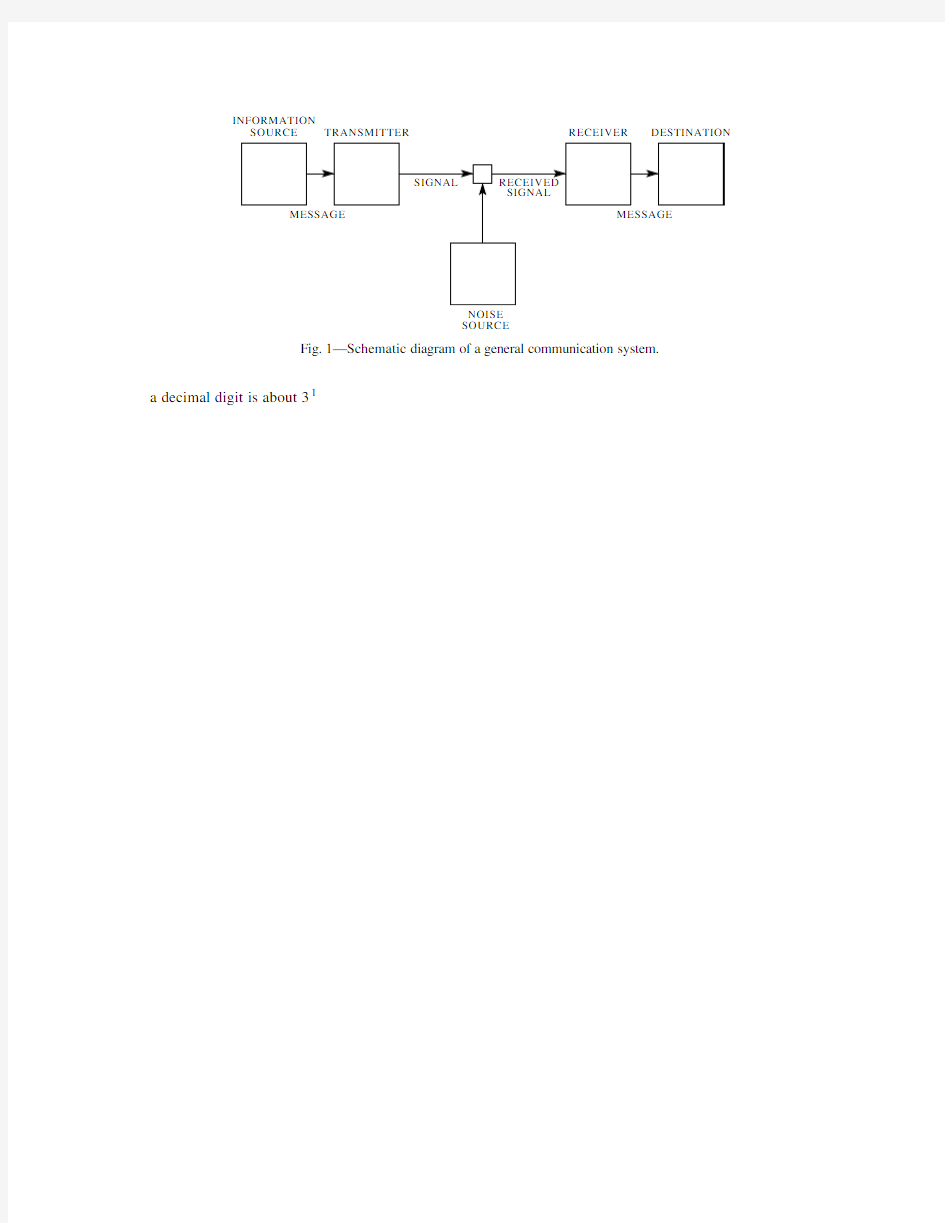
INFORMATION
SOURCE TRANSMITTER RECEIVER DESTINATION
NOISE
SOURCE
Fig.1—Schematic diagram of a general communication system.
a decimal digit is about31
physical counterparts.We may roughly classify communication systems into three main categories:discrete, continuous and mixed.By a discrete system we will mean one in which both the message and the signal are a sequence of discrete symbols.A typical case is telegraphy where the message is a sequence of letters
and the signal a sequence of dots,dashes and spaces.A continuous system is one in which the message and signal are both treated as continuous functions,e.g.,radio or television.A mixed system is one in which both discrete and continuous variables appear,e.g.,PCM transmission of speech.
We?rst consider the discrete case.This case has applications not only in communication theory,but also in the theory of computing machines,the design of telephone exchanges and other?elds.In addition
the discrete case forms a foundation for the continuous and mixed cases which will be treated in the second half of the paper.
PART I:DISCRETE NOISELESS SYSTEMS
1.T HE D ISCRETE N OISELESS C HANNEL
Teletype and telegraphy are two simple examples of a discrete channel for transmitting information.Gen-erally,a discrete channel will mean a system whereby a sequence of choices from a?nite set of elementary
symbols S1S n can be transmitted from one point to another.Each of the symbols S i is assumed to have a certain duration in time t i seconds(not necessarily the same for different S i,for example the dots and
dashes in telegraphy).It is not required that all possible sequences of the S i be capable of transmission on the system;certain sequences only may be allowed.These will be possible signals for the channel.Thus in telegraphy suppose the symbols are:(1)A dot,consisting of line closure for a unit of time and then line open for a unit of time;(2)A dash,consisting of three time units of closure and one unit open;(3)A letter space consisting of,say,three units of line open;(4)A word space of six units of line open.We might place the restriction on allowable sequences that no spaces follow each other(for if two letter spaces are adjacent, it is identical with a word space).The question we now consider is how one can measure the capacity of such a channel to transmit information.
In the teletype case where all symbols are of the same duration,and any sequence of the32symbols is allowed the answer is easy.Each symbol represents?ve bits of information.If the system transmits n symbols per second it is natural to say that the channel has a capacity of5n bits per second.This does not mean that the teletype channel will always be transmitting information at this rate—this is the maximum possible rate and whether or not the actual rate reaches this maximum depends on the source of information which feeds the channel,as will appear later.
In the more general case with different lengths of symbols and constraints on the allowed sequences,we make the following de?nition:
De?nition:The capacity C of a discrete channel is given by
log N T
C Lim
T∞
and therefore
C log X0
In case there are restrictions on allowed sequences we may still often obtain a difference equation of this type and?nd C from the characteristic equation.In the telegraphy case mentioned above
N t N t2N t4N t5N t7N t8N t10
as we see by counting sequences of symbols according to the last or next to the last symbol occurring. Hence C is log0where0is the positive root of12457810.Solving this we?nd C0539.
A very general type of restriction which may be placed on allowed sequences is the following:We imagine a number of possible states a1a2a m.For each state only certain symbols from the set S1S n can be transmitted(different subsets for the different states).When one of these has been transmitted the state changes to a new state depending both on the old state and the particular symbol transmitted.The telegraph case is a simple example of this.There are two states depending on whether or not a space was the last symbol transmitted.If so,then only a dot or a dash can be sent next and the state always changes. If not,any symbol can be transmitted and the state changes if a space is sent,otherwise it remains the same. The conditions can be indicated in a linear graph as shown in Fig.2.The junction points correspond to
the
Fig.2—Graphical representation of the constraints on telegraph symbols.
states and the lines indicate the symbols possible in a state and the resulting state.In Appendix1it is shown that if the conditions on allowed sequences can be described in this form C will exist and can be calculated in accordance with the following result:
Theorem1:Let b s i j be the duration of the s th symbol which is allowable in state i and leads to state j. Then the channel capacity C is equal to log W where W is the largest real root of the determinant equation:
∑s W b
s
i j i j0
where i j1if i j and is zero otherwise.
For example,in the telegraph case(Fig.2)the determinant is:
1W2W4
W3W6W2W410
On expansion this leads to the equation given above for this case.
2.T HE D ISCRETE S OURCE OF I NFORMATION
We have seen that under very general conditions the logarithm of the number of possible signals in a discrete channel increases linearly with time.The capacity to transmit information can be speci?ed by giving this rate of increase,the number of bits per second required to specify the particular signal used.
We now consider the information source.How is an information source to be described mathematically, and how much information in bits per second is produced in a given source?The main point at issue is the effect of statistical knowledge about the source in reducing the required capacity of the channel,by the use
of proper encoding of the information.In telegraphy,for example,the messages to be transmitted consist of sequences of letters.These sequences,however,are not completely random.In general,they form sentences and have the statistical structure of,say,English.The letter E occurs more frequently than Q,the sequence TH more frequently than XP,etc.The existence of this structure allows one to make a saving in time(or channel capacity)by properly encoding the message sequences into signal sequences.This is already done to a limited extent in telegraphy by using the shortest channel symbol,a dot,for the most common English letter E;while the infrequent letters,Q,X,Z are represented by longer sequences of dots and dashes.This idea is carried still further in certain commercial codes where common words and phrases are represented by four-or?ve-letter code groups with a considerable saving in average time.The standardized greeting and anniversary telegrams now in use extend this to the point of encoding a sentence or two into a relatively short sequence of numbers.
We can think of a discrete source as generating the message,symbol by symbol.It will choose succes-sive symbols according to certain probabilities depending,in general,on preceding choices as well as the particular symbols in question.A physical system,or a mathematical model of a system which produces such a sequence of symbols governed by a set of probabilities,is known as a stochastic process.3We may consider a discrete source,therefore,to be represented by a stochastic process.Conversely,any stochastic process which produces a discrete sequence of symbols chosen from a?nite set may be considered a discrete source.This will include such cases as:
1.Natural written languages such as English,German,Chinese.
2.Continuous information sources that have been rendered discrete by some quantizing process.For
example,the quantized speech from a PCM transmitter,or a quantized television signal.
3.Mathematical cases where we merely de?ne abstractly a stochastic process which generates a se-
quence of symbols.The following are examples of this last type of source.
(A)Suppose we have?ve letters A,B,C,D,E which are chosen each with probability.2,successive
choices being independent.This would lead to a sequence of which the following is a typical
example.
B D
C B C E C C C A
D C B D D A A
E C E E A
A B B D A E E C A C E E B A E E C B C E A D.
This was constructed with the use of a table of random numbers.4
(B)Using the same?ve letters let the probabilities be.4,.1,.2,.2,.1,respectively,with successive
choices independent.A typical message from this source is then:
A A A C D C
B D
C E A A
D A D A C
E D A
E A D C A B E D A D D C E C A A A A A D.
(C)A more complicated structure is obtained if successive symbols are not chosen independently
but their probabilities depend on preceding letters.In the simplest case of this type a choice
depends only on the preceding letter and not on ones before that.The statistical structure can
then be described by a set of transition probabilities p i j,the probability that letter i is followed
by letter j.The indices i and j range over all the possible symbols.A second equivalent way of
specifying the structure is to give the“digram”probabilities p i j,i.e.,the relative frequency of
the digram i j.The letter frequencies p i,(the probability of letter i),the transition probabilities 3See,for example,S.Chandrasekhar,“Stochastic Problems in Physics and Astronomy,”Reviews of Modern Physics,v.15,No.1, January1943,p.1.
4Kendall and Smith,Tables of Random Sampling Numbers,Cambridge,1939.
p i j and the digram probabilities p i j are related by the following formulas:
p i ∑j p i j
∑j p j i ∑j p j p j i
p i j p i p i j
∑j p i
j ∑i p i ∑i j
p i j 1As a speci?c example suppose there are three letters A,B,C with the probability tables:
p i j A B C 045i B 21151p i j
A
15
18270C 27
4135A typical message from this source is the following:
A B B A B A B A B A B A B A B B B A B B B B B A B A B A B A B A B B B A C A C A B
B A B B B B A B B A B A
C B B B A B A.
The next increase in complexity would involve trigram frequencies but no more.The choice of
a letter would depend on the preceding two letters but not on the message before that point.A set of trigram frequencies p i j k or equivalently a set of transition probabilities p i j k would be required.Continuing in this way one obtains successively more complicated stochastic pro-cesses.In the general n -gram case a set of n -gram probabilities p i 1i 2i n or of transition probabilities p i 1i 2i n 1i n is required to specify the statistical structure.
(D)Stochastic processes can also be de?ned which produce a text consisting of a sequence of
“words.”Suppose there are ?ve letters A,B,C,D,E and 16“words”in the language with associated probabilities:
.10A
.16BEBE .11CABED .04DEB .04ADEB
.04BED .05CEED .15DEED .05ADEE
.02BEED .08DAB .01EAB .01BADD .05CA .04DAD .05EE
Suppose successive “words”are chosen independently and are separated by a space.A typical message might be:
DAB EE A BEBE DEED DEB ADEE ADEE EE DEB BEBE BEBE BEBE ADEE BED DEED DEED CEED ADEE A DEED DEED BEBE CABED BEBE BED DAB DEED ADEB.
If all the words are of ?nite length this process is equivalent to one of the preceding type,but the description may be simpler in terms of the word structure and probabilities.We may also generalize here and introduce transition probabilities between words,etc.
These arti?cial languages are useful in constructing simple problems and examples to illustrate vari-ous possibilities.We can also approximate to a natural language by means of a series of simple arti?cial languages.The zero-order approximation is obtained by choosing all letters with the same probability and independently.The ?rst-order approximation is obtained by choosing successive letters independently but each letter having the same probability that it has in the natural language.5Thus,in the ?rst-order ap-proximation to English,E is chosen with probability .12(its frequency in normal English)and W with probability .02,but there is no in?uence between adjacent letters and no tendency to form the preferred
5Letter,
digram and trigram frequencies are given in Secret and Urgent by Fletcher Pratt,Blue Ribbon Books,1939.Word frequen-cies are tabulated in Relative Frequency of English Speech Sounds,G.Dewey,Harvard University Press,1923.
digrams such as TH,ED,etc.In the second-order approximation,digram structure is introduced.After a
letter is chosen,the next one is chosen in accordance with the frequencies with which the various letters
follow the?rst one.This requires a table of digram frequencies p i j.In the third-order approximation, trigram structure is introduced.Each letter is chosen with probabilities which depend on the preceding two
letters.
3.T HE S ERIES OF A PPROXIMATIONS TO E NGLISH
To give a visual idea of how this series of processes approaches a language,typical sequences in the approx-
imations to English have been constructed and are given below.In all cases we have assumed a27-symbol “alphabet,”the26letters and a space.
1.Zero-order approximation(symbols independent and equiprobable).
XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZL-
HJQD.
2.First-order approximation(symbols independent but with frequencies of English text).
OCRO HLI RGWR NMIELWIS EU LL NBNESEBY A TH EEI ALHENHTTPA OOBTTV A
NAH BRL.
3.Second-order approximation(digram structure as in English).
ON IE ANTSOUTINYS ARE T INCTORE ST BE S DEAMY ACHIN D ILONASIVE TU-
COOWE AT TEASONARE FUSO TIZIN ANDY TOBE SEACE CTISBE.
4.Third-order approximation(trigram structure as in English).
IN NO IST LAT WHEY CRATICT FROURE BIRS GROCID PONDENOME OF DEMONS-
TURES OF THE REPTAGIN IS REGOACTIONA OF CRE.
5.First-order word approximation.Rather than continue with tetragram,,n-gram structure it is easier
and better to jump at this point to word units.Here words are chosen independently but with their appropriate frequencies.
REPRESENTING AND SPEEDILY IS AN GOOD APT OR COME CAN DIFFERENT NAT-
URAL HERE HE THE A IN CAME THE TO OF TO EXPERT GRAY COME TO FURNISHES
THE LINE MESSAGE HAD BE THESE.
6.Second-order word approximation.The word transition probabilities are correct but no further struc-
ture is included.
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHAR-
ACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT
THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.
The resemblance to ordinary English text increases quite noticeably at each of the above steps.Note that these samples have reasonably good structure out to about twice the range that is taken into account in their construction.Thus in(3)the statistical process insures reasonable text for two-letter sequences,but four-letter sequences from the sample can usually be?tted into good sentences.In(6)sequences of four or more words can easily be placed in sentences without unusual or strained constructions.The particular sequence of ten words“attack on an English writer that the character of this”is not at all unreasonable.It appears then that a suf?ciently complex stochastic process will give a satisfactory representation of a discrete source.
The?rst two samples were constructed by the use of a book of random numbers in conjunction with
(for example2)a table of letter frequencies.This method might have been continued for(3),(4)and(5), since digram,trigram and word frequency tables are available,but a simpler equivalent method was used.
To construct(3)for example,one opens a book at random and selects a letter at random on the page.This letter is recorded.The book is then opened to another page and one reads until this letter is encountered. The succeeding letter is then recorded.Turning to another page this second letter is searched for and the succeeding letter recorded,etc.A similar process was used for(4),(5)and(6).It would be interesting if further approximations could be constructed,but the labor involved becomes enormous at the next stage.
4.G RAPHICAL R EPRESENTATION OF A M ARKOFF P ROCESS
Stochastic processes of the type described above are known mathematically as discrete Markoff processes and have been extensively studied in the literature.6The general case can be described as follows:There exist a?nite number of possible“states”of a system;S1S2S n.In addition there is a set of transition probabilities;p i j the probability that if the system is in state S i it will next go to state S j.To make this
Markoff process into an information source we need only assume that a letter is produced for each transition from one state to another.The states will correspond to the“residue of in?uence”from preceding letters.
The situation can be represented graphically as shown in Figs.3,4and5.The“states”are the
junction
Fig.3—A graph corresponding to the source in example B.
points in the graph and the probabilities and letters produced for a transition are given beside the correspond-ing line.Figure3is for the example B in Section2,while Fig.4corresponds to the example C.In Fig.
3
Fig.4—A graph corresponding to the source in example C.
there is only one state since successive letters are independent.In Fig.4there are as many states as letters. If a trigram example were constructed there would be at most n2states corresponding to the possible pairs of letters preceding the one being chosen.Figure5is a graph for the case of word structure in example D. Here S corresponds to the“space”symbol.
5.E RGODIC AND M IXED S OURCES
As we have indicated above a discrete source for our purposes can be considered to be represented by a Markoff process.Among the possible discrete Markoff processes there is a group with special properties of signi?cance in communication theory.This special class consists of the“ergodic”processes and we shall call the corresponding sources ergodic sources.Although a rigorous de?nition of an ergodic process is somewhat involved,the general idea is simple.In an ergodic process every sequence produced by the process 6For a detailed treatment see M.Fr′e chet,M′e thode des fonctions arbitraires.Th′e orie des′e v′e nements en cha??ne dans le cas d’un nombre?ni d’′e tats possibles.Paris,Gauthier-Villars,1938.
is the same in statistical properties.Thus the letter frequencies,digram frequencies,etc.,obtained from particular sequences,will,as the lengths of the sequences increase,approach de?nite limits independent of the particular sequence.Actually this is not true of every sequence but the set for which it is false has probability zero.Roughly the ergodic property means statistical homogeneity.
All the examples of arti?cial languages given above are ergodic.This property is related to the structure of the corresponding graph.If the graph has the following two properties7the corresponding process will be ergodic:
1.The graph does not consist of two isolated parts A and B such that it is impossible to go from junction
points in part A to junction points in part B along lines of the graph in the direction of arrows and also impossible to go from junctions in part B to junctions in part A.
2.A closed series of lines in the graph with all arrows on the lines pointing in the same orientation will
be called a“circuit.”The“length”of a circuit is the number of lines in it.Thus in Fig.5series BEBES is a circuit of length5.The second property required is that the greatest common divisor of the lengths of all circuits in the graph be
one.
If the?rst condition is satis?ed but the second one violated by having the greatest common divisor equal to d1,the sequences have a certain type of periodic structure.The various sequences fall into d different classes which are statistically the same apart from a shift of the origin(i.e.,which letter in the sequence is called letter1).By a shift of from0up to d1any sequence can be made statistically equivalent to any other.A simple example with d2is the following:There are three possible letters a b c.Letter a is
followed with either b or c with probabilities1
3respectively.Either b or c is always followed by letter
a.Thus a typical sequence is
a b a c a c a c a b a c a b a b a c a c
This type of situation is not of much importance for our work.
If the?rst condition is violated the graph may be separated into a set of subgraphs each of which satis?es the?rst condition.We will assume that the second condition is also satis?ed for each subgraph.We have in this case what may be called a“mixed”source made up of a number of pure components.The components correspond to the various subgraphs.If L1,L2,L3are the component sources we may write
L p1L1p2L2p3L3
7These are restatements in terms of the graph of conditions given in Fr′e chet.
where p i is the probability of the component source L i.
Physically the situation represented is this:There are several different sources L1,L2,L3which are each of homogeneous statistical structure(i.e.,they are ergodic).We do not know a priori which is to be used,but once the sequence starts in a given pure component L i,it continues inde?nitely according to the statistical structure of that component.
As an example one may take two of the processes de?ned above and assume p12and p28.A sequence from the mixed source
L2L18L2
would be obtained by choosing?rst L1or L2with probabilities.2and.8and after this choice generating a sequence from whichever was chosen.
Except when the contrary is stated we shall assume a source to be ergodic.This assumption enables one to identify averages along a sequence with averages over the ensemble of possible sequences(the probability of a discrepancy being zero).For example the relative frequency of the letter A in a particular in?nite sequence will be,with probability one,equal to its relative frequency in the ensemble of sequences.
If P i is the probability of state i and p i j the transition probability to state j,then for the process to be stationary it is clear that the P i must satisfy equilibrium conditions:
P j∑
i
P i p i j
In the ergodic case it can be shown that with any starting conditions the probabilities P j N of being in state j after N symbols,approach the equilibrium values as N∞.
6.C HOICE,U NCERTAINTY AND E NTROPY
We have represented a discrete information source as a Markoff process.Can we de?ne a quantity which will measure,in some sense,how much information is“produced”by such a process,or better,at what rate information is produced?
Suppose we have a set of possible events whose probabilities of occurrence are p1p2p n.These probabilities are known but that is all we know concerning which event will occur.Can we?nd a measure of how much“choice”is involved in the selection of the event or of how uncertain we are of the outcome?
If there is such a measure,say H p1p2p n,it is reasonable to require of it the following properties:
1.H should be continuous in the p i.
2.If all the p i are equal,p i1
2,p21
6
.On the right we?rst choose between two possibilities each with
probability1
3
,1
21
6
H1
2
1
3
1
2
is because this second choice only occurs half the time.
In Appendix2,the following result is established:
Theorem2:The only H satisfying the three above assumptions is of the form:
H K
n
∑
i1
p i log p i
where K is a positive constant.
This theorem,and the assumptions required for its proof,are in no way necessary for the present theory.
It is given chie?y to lend a certain plausibility to some of our later de?nitions.The real justi?cation of these de?nitions,however,will reside in their implications.
Quantities of the form H∑p i log p i(the constant K merely amounts to a choice of a unit of measure) play a central role in information theory as measures of information,choice and uncertainty.The form of H will be recognized as that of entropy as de?ned in certain formulations of statistical mechanics8where p i is
the probability of a system being in cell i of its phase space.H is then,for example,the H in Boltzmann’s famous H theorem.We shall call H∑p i log p i the entropy of the set of probabilities p1p n.If x is a chance variable we will write H x for its entropy;thus x is not an argument of a function but a label for a
number,to differentiate it from H y say,the entropy of the chance variable y.
The entropy in the case of two possibilities with probabilities p and q1p,namely
H p log p q log q
is plotted in Fig.7as a function of p.
H
BITS
p
Fig.7—Entropy in the case of two possibilities with probabilities p and1p.
The quantity H has a number of interesting properties which further substantiate it as a reasonable measure of choice or information.
1.H0if and only if all the p i but one are zero,this one having the value unity.Thus only when we
are certain of the outcome does H vanish.Otherwise H is positive.
2.For a given n,H is a maximum and equal to log n when all the p i are equal(i.e.,1
3.Suppose there are two events,x and y,in question with m possibilities for the?rst and n for the second. Let p i j be the probability of the joint occurrence of i for the?rst and j for the second.The entropy of the joint event is
H x y∑
i j
p i j log p i j
while
H x∑
i j p i j log∑
j
p i j
H y∑
i j p i j log∑
i
p i j
It is easily shown that
H x y H x H y
with equality only if the events are independent(i.e.,p i j p i p j).The uncertainty of a joint event is less than or equal to the sum of the individual uncertainties.
4.Any change toward equalization of the probabilities p1p2p n increases H.Thus if p1p2and we increase p1,decreasing p2an equal amount so that p1and p2are more nearly equal,then H increases. More generally,if we perform any“averaging”operation on the p i of the form
p i∑
j
a i j p j
where∑i a i j∑j a i j1,and all a i j0,then H increases(except in the special case where this transfor-mation amounts to no more than a permutation of the p j with H of course remaining the same).
5.Suppose there are two chance events x and y as in3,not necessarily independent.For any particular value i that x can assume there is a conditional probability p i j that y has the value j.This is given by
p i j
p i j
7.T HE E NTROPY OF AN I NFORMATION S OURCE
Consider a discrete source of the?nite state type considered above.For each possible state i there will be a set of probabilities p i j of producing the various possible symbols j.Thus there is an entropy H i for each state.The entropy of the source will be de?ned as the average of these H i weighted in accordance with the probability of occurrence of the states in question:
H∑
i
P i H i
∑
i j
P i p i j log p i j
This is the entropy of the source per symbol of text.If the Markoff process is proceeding at a de?nite time rate there is also an entropy per second
H∑
i
f i H i
where f i is the average frequency(occurrences per second)of state i.Clearly
H mH
where m is the average number of symbols produced per second.H or H measures the amount of informa-tion generated by the source per symbol or per second.If the logarithmic base is2,they will represent bits per symbol or per second.
If successive symbols are independent then H is simply∑p i log p i where p i is the probability of sym-bol i.Suppose in this case we consider a long message of N symbols.It will contain with high probability about p1N occurrences of the?rst symbol,p2N occurrences of the second,etc.Hence the probability of this particular message will be roughly
p p p1N
1p p2N
2
p p n N n
or
log p N∑
i
p i log p i
log p NH
H
log1p
N
H In other words we are almost certain to have
log p1
Theorem4:
Lim
N∞
log n q
N is the number of bits per symbol for
the speci?cation.The theorem says that for large N this will be independent of q and equal to H.The rate of growth of the logarithm of the number of reasonably probable sequences is given by H,regardless of our interpretation of“reasonably probable.”Due to these results,which are proved in Appendix3,it is possible for most purposes to treat the long sequences as though there were just2HN of them,each with a probability 2HN.
The next two theorems show that H and H can be determined by limiting operations directly from the statistics of the message sequences,without reference to the states and transition probabilities between states.
Theorem5:Let p B i be the probability of a sequence B i of symbols from the source.Let
G N
1
N
N ∑
n1
F n
F N
G N
and Lim N∞F N H.
These results are derived in Appendix3.They show that a series of approximations to H can be obtained
by considering only the statistical structure of the sequences extending over12N symbols.F N is the
better approximation.In fact F N is the entropy of the N th order approximation to the source of the type discussed above.If there are no statistical in?uences extending over more than N symbols,that is if the
conditional probability of the next symbol knowing the preceding N1is not changed by a knowledge of
any before that,then F N H.F N of course is the conditional entropy of the next symbol when the N1 preceding ones are known,while G N is the entropy per symbol of blocks of N symbols.
The ratio of the entropy of a source to the maximum value it could have while still restricted to the same symbols will be called its relative entropy.This is the maximum compression possible when we encode into the same alphabet.One minus the relative entropy is the redundancy.The redundancy of ordinary English, not considering statistical structure over greater distances than about eight letters,is roughly50%.This means that when we write English half of what we write is determined by the structure of the language and half is chosen freely.The?gure50%was found by several independent methods which all gave results in
this neighborhood.One is by calculation of the entropy of the approximations to English.A second method
is to delete a certain fraction of the letters from a sample of English text and then let someone attempt to
restore them.If they can be restored when50%are deleted the redundancy must be greater than50%.A third method depends on certain known results in cryptography.
Two extremes of redundancy in English prose are represented by Basic English and by James Joyce’s
book“Finnegans Wake”.The Basic English vocabulary is limited to850words and the redundancy is very high.This is re?ected in the expansion that occurs when a passage is translated into Basic English.Joyce
on the other hand enlarges the vocabulary and is alleged to achieve a compression of semantic content.
The redundancy of a language is related to the existence of crossword puzzles.If the redundancy is
zero any sequence of letters is a reasonable text in the language and any two-dimensional array of letters
forms a crossword puzzle.If the redundancy is too high the language imposes too many constraints for large crossword puzzles to be possible.A more detailed analysis shows that if we assume the constraints imposed
by the language are of a rather chaotic and random nature,large crossword puzzles are just possible when
the redundancy is50%.If the redundancy is33%,three-dimensional crossword puzzles should be possible, etc.
8.R EPRESENTATION OF THE E NCODING AND D ECODING O PERATIONS
We have yet to represent mathematically the operations performed by the transmitter and receiver in en-
coding and decoding the information.Either of these will be called a discrete transducer.The input to the transducer is a sequence of input symbols and its output a sequence of output symbols.The transducer may
have an internal memory so that its output depends not only on the present input symbol but also on the past
history.We assume that the internal memory is?nite,i.e.,there exist a?nite number m of possible states of the transducer and that its output is a function of the present state and the present input symbol.The next
state will be a second function of these two quantities.Thus a transducer can be described by two functions:
y n f x n n
n1g x n n
where
x n is the n th input symbol,
n is the state of the transducer when the n th input symbol is introduced,
y n is the output symbol(or sequence of output symbols)produced when x n is introduced if the state is n.
If the output symbols of one transducer can be identi?ed with the input symbols of a second,they can be
connected in tandem and the result is also a transducer.If there exists a second transducer which operates on the output of the?rst and recovers the original input,the?rst transducer will be called non-singular and
the second will be called its inverse.
Theorem7:The output of a?nite state transducer driven by a?nite state statistical source is a?nite state statistical source,with entropy(per unit time)less than or equal to that of the input.If the transducer is non-singular they are equal.
Let represent the state of the source,which produces a sequence of symbols x i;and let be the state of
the transducer,which produces,in its output,blocks of symbols y j.The combined system can be represented by the“product state space”of pairs.Two points in the space11and22,are connected by a line if1can produce an x which changes1to2,and this line is given the probability of that x in this
case.The line is labeled with the block of y j symbols produced by the transducer.The entropy of the output can be calculated as the weighted sum over the states.If we sum?rst on each resulting term is less than or equal to the corresponding term for,hence the entropy is not increased.If the transducer is non-singular let its output be connected to the inverse transducer.If H1,H2and H3are the output entropies of the source, the?rst and second transducers respectively,then H1H2H3H1and therefore H1H2.
Suppose we have a system of constraints on possible sequences of the type which can be represented by a linear graph as in Fig.2.If probabilities p s i j were assigned to the various lines connecting state i to state j this would become a source.There is one particular assignment which maximizes the resulting entropy(see Appendix4).
Theorem8:Let the system of constraints considered as a channel have a capacity C log W.If we assign
p s i j
B j
H
symbols per second over the channel where is arbitrarily small.It is not possible to transmit at an average rate greater than
C
H cannot be exceeded,may be proved by noting that the entropy
of the channel input per second is equal to that of the source,since the transmitter must be non-singular,and also this entropy cannot exceed the channel capacity.Hence H C and the number of symbols per second H H C H.
The?rst part of the theorem will be proved in two different ways.The?rst method is to consider the set of all sequences of N symbols produced by the source.For N large we can divide these into two groups, one containing less than2H N members and the second containing less than2RN members(where R is the logarithm of the number of different symbols)and having a total probability less than.As N increases and approach zero.The number of signals of duration T in the channel is greater than2C T with small when T is large.if we choose
T
H
C
N
where is small.The mean rate of transmission in message symbols per second will then be greater than
1T
N 1
1H
C
1
As N increases,and approach zero and the rate approaches
C
p s
m s1log21
2m s
p s1
2m s larger and their binary expansions therefore differ in the?rst m s places.Consequently all
the codes are different and it is possible to recover the message from its code.If the channel sequences are not already sequences of binary digits,they can be ascribed binary numbers in an arbitrary fashion and the binary code thus translated into signals suitable for the channel.
The average number H of binary digits used per symbol of original message is easily estimated.We have
H
1
N ∑log21
N
∑m s p s1
p s
p s
and therefore,
G N H G N
1
N plus the difference between the true entropy H and the entropy G N calculated for
sequences of length N.The per cent excess time needed over the ideal is therefore less than
G N
HN
1
This method of encoding is substantially the same as one found independently by R.M.Fano.9His method is to arrange the messages of length N in order of decreasing probability.Divide this series into two groups of as nearly equal probability as possible.If the message is in the?rst group its?rst binary digit will be0,otherwise1.The groups are similarly divided into subsets of nearly equal probability and the particular subset determines the second binary digit.This process is continued until each subset contains only one message.It is easily seen that apart from minor differences(generally in the last digit)this amounts to the same thing as the arithmetic process described above.
10.D ISCUSSION AND E XAMPLES
In order to obtain the maximum power transfer from a generator to a load,a transformer must in general be introduced so that the generator as seen from the load has the load resistance.The situation here is roughly analogous.The transducer which does the encoding should match the source to the channel in a statistical sense.The source as seen from the channel through the transducer should have the same statistical structure 9Technical Report No.65,The Research Laboratory of Electronics,M.I.T.,March17,1949.
as the source which maximizes the entropy in the channel.The content of Theorem9is that,although an exact match is not in general possible,we can approximate it as closely as desired.The ratio of the actual rate of transmission to the capacity C may be called the ef?ciency of the coding system.This is of course equal to the ratio of the actual entropy of the channel symbols to the maximum possible entropy.
In general,ideal or nearly ideal encoding requires a long delay in the transmitter and receiver.In the noiseless case which we have been considering,the main function of this delay is to allow reasonably good matching of probabilities to corresponding lengths of sequences.With a good code the logarithm of the reciprocal probability of a long message must be proportional to the duration of the corresponding signal,in fact
log p1
2,1
8
,1
2log1
4
log1
8
log1
4
bits per symbol
Thus we can approximate a coding system to encode messages from this source into binary digits with an average of7
211
8
37
2
,1
4
binary symbols per original letter,the entropies on a time
basis are the same.The maximum possible entropy for the original set is log42,occurring when A,B,C,
D have probabilities1
4,1
4
.Hence the relative entropy is7
This double process then encodes the original message into the same symbols but with an average compres-sion ratio7
p
In such a case one can construct a fairly good coding of the message on a0,1channel by sending a special sequence,say0000,for the infrequent symbol A and then a sequence indicating the number of B’s following it.This could be indicated by the binary representation with all numbers containing the special sequence deleted.All numbers up to16are represented as usual;16is represented by the next binary number after16 which does not contain four zeros,namely1710001,etc.
It can be shown that as p0the coding approaches ideal provided the length of the special sequence is properly adjusted.
PART II:THE DISCRETE CHANNEL WITH NOISE
11.R EPRESENTATION OF A N OISY D ISCRETE C HANNEL
We now consider the case where the signal is perturbed by noise during transmission or at one or the other of the terminals.This means that the received signal is not necessarily the same as that sent out by the transmitter.Two cases may be distinguished.If a particular transmitted signal always produces the same received signal,i.e.,the received signal is a de?nite function of the transmitted signal,then the effect may be called distortion.If this function has an inverse—no two transmitted signals producing the same received signal—distortion may be corrected,at least in principle,by merely performing the inverse functional operation on the received signal.
The case of interest here is that in which the signal does not always undergo the same change in trans-mission.In this case we may assume the received signal E to be a function of the transmitted signal S and a second variable,the noise N.
E f S N
The noise is considered to be a chance variable just as the message was above.In general it may be repre-sented by a suitable stochastic process.The most general type of noisy discrete channel we shall consider is a generalization of the?nite state noise-free channel described previously.We assume a?nite number of states and a set of probabilities
p i j
This is the probability,if the channel is in state and symbol i is transmitted,that symbol j will be received and the channel left in state.Thus and range over the possible states,i over the possible transmitted signals and j over the possible received signals.In the case where successive symbols are independently per-turbed by the noise there is only one state,and the channel is described by the set of transition probabilities p i j,the probability of transmitted symbol i being received as j.
If a noisy channel is fed by a source there are two statistical processes at work:the source and the noise. Thus there are a number of entropies that can be calculated.First there is the entropy H x of the source or of the input to the channel(these will be equal if the transmitter is non-singular).The entropy of the output of the channel,i.e.,the received signal,will be denoted by H y.In the noiseless case H y H x. The joint entropy of input and output will be H xy.Finally there are two conditional entropies H x y and H y x,the entropy of the output when the input is known and conversely.Among these quantities we have the relations
H x y H x H x y H y H y x
All of these entropies can be measured on a per-second or a per-symbol basis.
12.E QUIVOCATION AND C HANNEL C APACITY
If the channel is noisy it is not in general possible to reconstruct the original message or the transmitted signal with certainty by any operation on the received signal E.There are,however,ways of transmitting the information which are optimal in combating noise.This is the problem which we now consider.
Suppose there are two possible symbols0and1,and we are transmitting at a rate of1000symbols per second with probabilities p0p11
2whatever was transmitted and similarly for0.
Then about half of the received symbols are correct due to chance alone,and we would be giving the system
credit for transmitting500bits per second while actually no information is being transmitted at all.Equally “good”transmission would be obtained by dispensing with the channel entirely and?ipping a coin at the receiving point.
Evidently the proper correction to apply to the amount of information transmitted is the amount of this information which is missing in the received signal,or alternatively the uncertainty when we have received a signal of what was actually sent.From our previous discussion of entropy as a measure of uncertainty it seems reasonable to use the conditional entropy of the message,knowing the received signal,as a measure of this missing information.This is indeed the proper de?nition,as we shall see later.Following this idea the rate of actual transmission,R,would be obtained by subtracting from the rate of production(i.e.,the entropy of the source)the average rate of conditional entropy.
R H x H y x
The conditional entropy H y x will,for convenience,be called the equivocation.It measures the average ambiguity of the received signal.
In the example considered above,if a0is received the a posteriori probability that a0was transmitted is.99,and that a1was transmitted is.01.These?gures are reversed if a1is received.Hence
H y x99log99001log001
081bits/symbol
or81bits per second.We may say that the system is transmitting at a rate100081919bits per second. In the extreme case where a0is equally likely to be received as a0or1and similarly for1,the a posteriori
probabilities are1
2
and
H y x1212
1bit per symbol
or1000bits per second.The rate of transmission is then0as it should be.
The following theorem gives a direct intuitive interpretation of the equivocation and also serves to justify it as the unique appropriate measure.We consider a communication system and an observer(or auxiliary device)who can see both what is sent and what is recovered(with errors due to noise).This observer notes the errors in the recovered message and transmits data to the receiving point over a“correction channel”to enable the receiver to correct the errors.The situation is indicated schematically in Fig.8.
Theorem10:If the correction channel has a capacity equal to H y x it is possible to so encode the correction data as to send it over this channel and correct all but an arbitrarily small fraction of the errors. This is not possible if the channel capacity is less than H y x.
从实践的角度探讨在日语教学中多媒体课件的应用 在今天中国的许多大学,为适应现代化,信息化的要求,建立了设备完善的适应多媒体教学的教室。许多学科的研究者及现场教员也积极致力于多媒体软件的开发和利用。在大学日语专业的教学工作中,教科书、磁带、粉笔为主流的传统教学方式差不多悄然向先进的教学手段而进展。 一、多媒体课件和精品课程的进展现状 然而,目前在专业日语教学中能够利用的教学软件并不多见。比如在中国大学日语的专业、第二外語用教科书常见的有《新编日语》(上海外语教育出版社)、《中日交流标准日本語》(初级、中级)(人民教育出版社)、《新编基础日语(初級、高級)》(上海译文出版社)、《大学日本语》(四川大学出版社)、《初级日语》《中级日语》(北京大学出版社)、《新世纪大学日语》(外语教学与研究出版社)、《综合日语》(北京大学出版社)、《新编日语教程》(华东理工大学出版社)《新编初级(中级)日本语》(吉林教育出版社)、《新大学日本语》(大连理工大学出版社)、《新大学日语》(高等教育出版社)、《现代日本语》(上海外语教育出版社)、《基础日语》(复旦大学出版社)等等。配套教材以录音磁带、教学参考、习题集为主。只有《中日交流標準日本語(初級上)》、《初級日语》、《新编日语教程》等少数教科书配备了多媒体DVD视听教材。 然而这些试听教材,有的内容为日语普及读物,并不适合专业外语课堂教学。比如《新版中日交流标准日本语(初级上)》,有的尽管DVD视听教材中有丰富的动画画面和语音练习。然而,课堂操作则花费时刻长,不利于教师重点指导,更加适合学生的课余练习。比如北京大学的《初级日语》等。在这种情形下,许多大学的日语专业致力于教材的自主开发。 其中,有些大学的还推出精品课程,取得了专门大成绩。比如天津外国语学院的《新编日语》多媒体精品课程为2007年被评为“国家级精品课”。目前已被南开大学外国语学院、成都理工大学日语系等全国40余所大学推广使用。
Unit1 Americans believe no one stands still. If you are not moving ahead, you are falling behind. This attitude results in a nation of people committed to researching, experimenting and exploring. Time is one of the two elements that Americans save carefully, the other being labor. "We are slaves to nothing but the clock,” it has been said. Time is treated as if it were something almost real. We budget it, save it, waste it, steal it, kill it, cut it, account for it; we also charge for it. It is a precious resource. Many people have a rather acute sense of the shortness of each lifetime. Once the sands have run out of a person’s hourglass, they cannot be replaced. We want every minute to count. A foreigner’s first impression of the U.S. is li kely to be that everyone is in a rush -- often under pressure. City people always appear to be hurrying to get where they are going, restlessly seeking attention in a store, or elbowing others as they try to complete their shopping. Racing through daytime meals is part of the pace
新视野三版读写B2U4Text A College sweethearts 1I smile at my two lovely daughters and they seem so much more mature than we,their parents,when we were college sweethearts.Linda,who's21,had a boyfriend in her freshman year she thought she would marry,but they're not together anymore.Melissa,who's19,hasn't had a steady boyfriend yet.My daughters wonder when they will meet"The One",their great love.They think their father and I had a classic fairy-tale romance heading for marriage from the outset.Perhaps,they're right but it didn't seem so at the time.In a way, love just happens when you least expect it.Who would have thought that Butch and I would end up getting married to each other?He became my boyfriend because of my shallow agenda:I wanted a cute boyfriend! 2We met through my college roommate at the university cafeteria.That fateful night,I was merely curious,but for him I think it was love at first sight."You have beautiful eyes",he said as he gazed at my face.He kept staring at me all night long.I really wasn't that interested for two reasons.First,he looked like he was a really wild boy,maybe even dangerous.Second,although he was very cute,he seemed a little weird. 3Riding on his bicycle,he'd ride past my dorm as if"by accident"and pretend to be surprised to see me.I liked the attention but was cautious about his wild,dynamic personality.He had a charming way with words which would charm any girl.Fear came over me when I started to fall in love.His exciting"bad boy image"was just too tempting to resist.What was it that attracted me?I always had an excellent reputation.My concentration was solely on my studies to get superior grades.But for what?College is supposed to be a time of great learning and also some fun.I had nearly achieved a great education,and graduation was just one semester away.But I hadn't had any fun;my life was stale with no component of fun!I needed a boyfriend.Not just any boyfriend.He had to be cute.My goal that semester became: Be ambitious and grab the cutest boyfriend I can find. 4I worried what he'd think of me.True,we lived in a time when a dramatic shift in sexual attitudes was taking place,but I was a traditional girl who wasn't ready for the new ways that seemed common on campus.Butch looked superb!I was not immune to his personality,but I was scared.The night when he announced to the world that I was his girlfriend,I went along
Unit 1 1学习外语是我一生中最艰苦也是最有意义的经历之一。虽然时常遭遇挫折,但却非常有价值。 2我学外语的经历始于初中的第一堂英语课。老师很慈祥耐心,时常表扬学生。由于这种积极的教学方法,我踊跃回答各种问题,从不怕答错。两年中,我的成绩一直名列前茅。 3到了高中后,我渴望继续学习英语。然而,高中时的经历与以前大不相同。以前,老师对所有的学生都很耐心,而新老师则总是惩罚答错的学生。每当有谁回答错了,她就会用长教鞭指着我们,上下挥舞大喊:“错!错!错!”没有多久,我便不再渴望回答问题了。我不仅失去了回答问题的乐趣,而且根本就不想再用英语说半个字。 4好在这种情况没持续多久。到了大学,我了解到所有学生必须上英语课。与高中老师不。大学英语老师非常耐心和蔼,而且从来不带教鞭!不过情况却远不尽如人意。由于班大,每堂课能轮到我回答的问题寥寥无几。上了几周课后,我还发现许多同学的英语说得比我要好得多。我开始产生一种畏惧感。虽然原因与高中时不同,但我却又一次不敢开口了。看来我的英语水平要永远停步不前了。 5直到几年后我有机会参加远程英语课程,情况才有所改善。这种课程的媒介是一台电脑、一条电话线和一个调制解调器。我很快配齐了必要的设备并跟一个朋友学会了电脑操作技术,于是我每周用5到7天在网上的虚拟课堂里学习英语。 6网上学习并不比普通的课堂学习容易。它需要花许多的时间,需要学习者专心自律,以跟上课程进度。我尽力达到课程的最低要求,并按时完成作业。 7我随时随地都在学习。不管去哪里,我都随身携带一本袖珍字典和笔记本,笔记本上记着我遇到的生词。我学习中出过许多错,有时是令人尴尬的错误。有时我会因挫折而哭泣,有时甚至想放弃。但我从未因别的同学英语说得比我快而感到畏惧,因为在电脑屏幕上作出回答之前,我可以根据自己的需要花时间去琢磨自己的想法。突然有一天我发现自己什么都懂了,更重要的是,我说起英语来灵活自如。尽管我还是常常出错,还有很多东西要学,但我已尝到了刻苦学习的甜头。 8学习外语对我来说是非常艰辛的经历,但它又无比珍贵。它不仅使我懂得了艰苦努力的意义,而且让我了解了不同的文化,让我以一种全新的思维去看待事物。学习一门外语最令人兴奋的收获是我能与更多的人交流。与人交谈是我最喜欢的一项活动,新的语言使我能与陌生人交往,参与他们的谈话,并建立新的难以忘怀的友谊。由于我已能说英语,别人讲英语时我不再茫然不解了。我能够参与其中,并结交朋友。我能与人交流,并能够弥合我所说的语言和所处的文化与他们的语言和文化之间的鸿沟。 III. 1. rewarding 2. communicate 3. access 4. embarrassing 5. positive 6. commitment 7. virtual 8. benefits 9. minimum 10. opportunities IV. 1. up 2. into 3. from 4. with 5. to 6. up 7. of 8. in 9. for 10.with V. 1.G 2.B 3.E 4.I 5.H 6.K 7.M 8.O 9.F 10.C Sentence Structure VI. 1. Universities in the east are better equipped, while those in the west are relatively poor. 2. Allan Clark kept talking the price up, while Wilkinson kept knocking it down. 3. The husband spent all his money drinking, while his wife saved all hers for the family. 4. Some guests spoke pleasantly and behaved politely, while others wee insulting and impolite. 5. Outwardly Sara was friendly towards all those concerned, while inwardly she was angry. VII. 1. Not only did Mr. Smith learn the Chinese language, but he also bridged the gap between his culture and ours. 2. Not only did we learn the technology through the online course, but we also learned to communicate with friends in English. 3. Not only did we lose all our money, but we also came close to losing our lives.
新大学日语简明教程课文翻译 第21课 一、我的留学生活 我从去年12月开始学习日语。已经3个月了。每天大约学30个新单词。每天学15个左右的新汉字,但总记不住。假名已经基本记住了。 简单的会话还可以,但较难的还说不了。还不能用日语发表自己的意见。既不能很好地回答老师的提问,也看不懂日语的文章。短小、简单的信写得了,但长的信写不了。 来日本不久就迎来了新年。新年时,日本的少女们穿着美丽的和服,看上去就像新娘。非常冷的时候,还是有女孩子穿着裙子和袜子走在大街上。 我在日本的第一个新年过得很愉快,因此很开心。 现在学习忙,没什么时间玩,但周末常常运动,或骑车去公园玩。有时也邀朋友一起去。虽然我有国际驾照,但没钱,买不起车。没办法,需要的时候就向朋友借车。有几个朋友愿意借车给我。 二、一个房间变成三个 从前一直认为睡在褥子上的是日本人,美国人都睡床铺,可是听说近来纽约等大都市的年轻人不睡床铺,而是睡在褥子上,是不是突然讨厌起床铺了? 日本人自古以来就睡在褥子上,那自有它的原因。人们都说日本人的房子小,从前,很少有人在自己的房间,一家人住在一个小房间里是常有的是,今天仍然有人过着这样的生活。 在仅有的一个房间哩,如果要摆下全家人的床铺,就不能在那里吃饭了。这一点,褥子很方便。早晨,不需要褥子的时候,可以收起来。在没有了褥子的房间放上桌子,当作饭厅吃早饭。来客人的话,就在那里喝茶;孩子放学回到家里,那房间就成了书房。而后,傍晚又成为饭厅。然后收起桌子,铺上褥子,又成为了全家人睡觉的地方。 如果是床铺的话,除了睡觉的房间,还需要吃饭的房间和书房等,但如果使用褥子,一个房间就可以有各种用途。 据说从前,在纽约等大都市的大学学习的学生也租得起很大的房间。但现在房租太贵,租不起了。只能住更便宜、更小的房间。因此,似乎开始使用睡觉时作床,白天折小能成为椅子的、方便的褥子。
新视野大学英语第一册Unit 1课文翻译 学习外语是我一生中最艰苦也是最有意义的经历之一。 虽然时常遭遇挫折,但却非常有价值。 我学外语的经历始于初中的第一堂英语课。 老师很慈祥耐心,时常表扬学生。 由于这种积极的教学方法,我踊跃回答各种问题,从不怕答错。 两年中,我的成绩一直名列前茅。 到了高中后,我渴望继续学习英语。然而,高中时的经历与以前大不相同。 以前,老师对所有的学生都很耐心,而新老师则总是惩罚答错的学生。 每当有谁回答错了,她就会用长教鞭指着我们,上下挥舞大喊:“错!错!错!” 没有多久,我便不再渴望回答问题了。 我不仅失去了回答问题的乐趣,而且根本就不想再用英语说半个字。 好在这种情况没持续多久。 到了大学,我了解到所有学生必须上英语课。 与高中老师不同,大学英语老师非常耐心和蔼,而且从来不带教鞭! 不过情况却远不尽如人意。 由于班大,每堂课能轮到我回答的问题寥寥无几。 上了几周课后,我还发现许多同学的英语说得比我要好得多。 我开始产生一种畏惧感。 虽然原因与高中时不同,但我却又一次不敢开口了。 看来我的英语水平要永远停步不前了。 直到几年后我有机会参加远程英语课程,情况才有所改善。 这种课程的媒介是一台电脑、一条电话线和一个调制解调器。 我很快配齐了必要的设备并跟一个朋友学会了电脑操作技术,于是我每周用5到7天在网上的虚拟课堂里学习英语。 网上学习并不比普通的课堂学习容易。 它需要花许多的时间,需要学习者专心自律,以跟上课程进度。 我尽力达到课程的最低要求,并按时完成作业。 我随时随地都在学习。 不管去哪里,我都随身携带一本袖珍字典和笔记本,笔记本上记着我遇到的生词。 我学习中出过许多错,有时是令人尴尬的错误。 有时我会因挫折而哭泣,有时甚至想放弃。 但我从未因别的同学英语说得比我快而感到畏惧,因为在电脑屏幕上作出回答之前,我可以根据自己的需要花时间去琢磨自己的想法。 突然有一天我发现自己什么都懂了,更重要的是,我说起英语来灵活自如。 尽管我还是常常出错,还有很多东西要学,但我已尝到了刻苦学习的甜头。 学习外语对我来说是非常艰辛的经历,但它又无比珍贵。 它不仅使我懂得了艰苦努力的意义,而且让我了解了不同的文化,让我以一种全新的思维去看待事物。 学习一门外语最令人兴奋的收获是我能与更多的人交流。 与人交谈是我最喜欢的一项活动,新的语言使我能与陌生人交往,参与他们的谈话,并建立新的难以忘怀的友谊。 由于我已能说英语,别人讲英语时我不再茫然不解了。 我能够参与其中,并结交朋友。
习惯与礼仪 我是个漫画家,对旁人细微的动作、不起眼的举止等抱有好奇。所以,我在国外只要做错一点什么,立刻会比旁人更为敏锐地感觉到那个国家的人们对此作出的反应。 譬如我多次看到过,欧美人和中国人见到我们日本人吸溜吸溜地出声喝汤而面露厌恶之色。过去,日本人坐在塌塌米上,在一张低矮的食案上用餐,餐具离嘴较远。所以,养成了把碗端至嘴边吸食的习惯。喝羹匙里的东西也象吸似的,声声作响。这并非哪一方文化高或低,只是各国的习惯、礼仪不同而已。 日本人坐在椅子上围桌用餐是1960年之后的事情。当时,还没有礼仪规矩,甚至有人盘着腿吃饭。外国人看见此景大概会一脸厌恶吧。 韩国女性就座时,单腿翘起。我认为这种姿势很美,但习惯于双膝跪坐的日本女性大概不以为然,而韩国女性恐怕也不认为跪坐为好。 日本等多数亚洲国家,常有人习惯在路上蹲着。欧美人会联想起狗排便的姿势而一脸厌恶。 日本人常常把手放在小孩的头上说“好可爱啊!”,而大部分外国人会不愿意。 如果向回教国家的人们劝食猪肉和酒,或用左手握手、递东西,会不受欢迎的。当然,饭菜也用右手抓着吃。只有从公用大盘往自己的小盘里分食用的公勺是用左手拿。一旦搞错,用黏糊糊的右手去拿,
会遭人厌恶。 在欧美,对不受欢迎的客人不说“请脱下外套”,所以电视剧中的侦探哥隆波总是穿着外套。访问日本家庭时,要在门厅外脱掉外套后进屋。穿到屋里会不受欢迎的。 这些习惯只要了解就不会出问题,如果因为不知道而遭厌恶、憎恨,实在心里难受。 过去,我曾用色彩图画和简短的文字画了一本《关键时刻的礼仪》(新潮文库)。如今越发希望用各国语言翻译这本书。以便能对在日本的外国人有所帮助。同时希望有朝一日以漫画的形式画一本“世界各国的习惯与礼仪”。 练习答案 5、 (1)止める並んでいる見ているなる着色した (2)拾った入っていた行ったしまった始まっていた
新视野大学英语第三版第二册读写课文翻译 Unit 1 Text A 一堂难忘的英语课 1 如果我是唯一一个还在纠正小孩英语的家长,那么我儿子也许是对的。对他而言,我是一个乏味的怪物:一个他不得不听其教诲的父亲,一个还沉湎于语法规则的人,对此我儿子似乎颇为反感。 2 我觉得我是在最近偶遇我以前的一位学生时,才开始对这个问题认真起来的。这个学生刚从欧洲旅游回来。我满怀着诚挚期待问她:“欧洲之行如何?” 3 她点了三四下头,绞尽脑汁,苦苦寻找恰当的词语,然后惊呼:“真是,哇!” 4 没了。所有希腊文明和罗马建筑的辉煌居然囊括于一个浓缩的、不完整的语句之中!我的学生以“哇!”来表示她的惊叹,我只能以摇头表达比之更强烈的忧虑。 5 关于正确使用英语能力下降的问题,有许多不同的故事。学生的确本应该能够区分诸如their/there/they're之间的不同,或区别complimentary 跟complementary之间显而易见的差异。由于这些知识缺陷,他们承受着大部分不该承受的批评和指责,因为舆论认为他们应该学得更好。 6 学生并不笨,他们只是被周围所看到和听到的语言误导了。举例来说,杂货店的指示牌会把他们引向stationary(静止处),虽然便笺本、相册、和笔记本等真正的stationery(文具用品)并没有被钉在那儿。朋友和亲人常宣称They've just ate。实际上,他们应该说They've just eaten。因此,批评学生不合乎情理。 7 对这种缺乏语言功底而引起的负面指责应归咎于我们的学校。学校应对英语熟练程度制定出更高的标准。可相反,学校只教零星的语法,高级词汇更是少之又少。还有就是,学校的年轻教师显然缺乏这些重要的语言结构方面的知识,因为他们过去也没接触过。学校有责任教会年轻人进行有效的语言沟通,可他们并没把语言的基本框架——准确的语法和恰当的词汇——充分地传授给学生。
新视野大学英语1课文翻译 1下午好!作为校长,我非常自豪地欢迎你们来到这所大学。你们所取得的成就是你们自己多年努力的结果,也是你们的父母和老师们多年努力的结果。在这所大学里,我们承诺将使你们学有所成。 2在欢迎你们到来的这一刻,我想起自己高中毕业时的情景,还有妈妈为我和爸爸拍的合影。妈妈吩咐我们:“姿势自然点。”“等一等,”爸爸说,“把我递给他闹钟的情景拍下来。”在大学期间,那个闹钟每天早晨叫醒我。至今它还放在我办公室的桌子上。 3让我来告诉你们一些你们未必预料得到的事情。你们将会怀念以前的生活习惯,怀念父母曾经提醒你们要刻苦学习、取得佳绩。你们可能因为高中生活终于结束而喜极而泣,你们的父母也可能因为终于不用再给你们洗衣服而喜极而泣!但是要记住:未来是建立在过去扎实的基础上的。 4对你们而言,接下来的四年将会是无与伦比的一段时光。在这里,你们拥有丰富的资源:有来自全国各地的有趣的学生,有学识渊博又充满爱心的老师,有综合性图书馆,有完备的运动设施,还有针对不同兴趣的学生社团——从文科社团到理科社团、到社区服务等等。你们将自由地探索、学习新科目。你们要学着习惯点灯熬油,学着结交充满魅力的人,学着去追求新的爱好。我想鼓励你们充分利用这一特殊的经历,并用你们的干劲和热情去收获这一机会所带来的丰硕成果。 5有这么多课程可供选择,你可能会不知所措。你不可能选修所有的课程,但是要尽可能体验更多的课程!大学里有很多事情可做可学,每件事情都会为你提供不同视角来审视世界。如果我只能给你们一条选课建议的话,那就是:挑战自己!不要认为你早就了解自己对什么样的领域最感兴趣。选择一些你从未接触过的领域的课程。这样,你不仅会变得更加博学,而且更有可能发现一个你未曾想到的、能成就你未来的爱好。一个绝佳的例子就是时装设计师王薇薇,她最初学的是艺术史。随着时间的推移,王薇薇把艺术史研究和对时装的热爱结合起来,并将其转化为对设计的热情,从而使她成为全球闻名的设计师。 6在大学里,一下子拥有这么多新鲜体验可能不会总是令人愉快的。在你的宿舍楼里,住在你隔壁寝室的同学可能会反复播放同一首歌,令你头痛欲裂!你可能喜欢早起,而你的室友却是个夜猫子!尽管如此,你和你的室友仍然可能成
新视野大学英语2课文翻译(Unit1-Unit7) Unit 1 Section A 时间观念强的美国人 Para. 1 美国人认为没有人能停止不前。如果你不求进取,你就会落伍。这种态度造就了一个投身于研究、实验和探索的民族。时间是美国人注意节约的两个要素之一,另一个是劳力。 Para. 2 人们一直说:“只有时间才能支配我们。”人们似乎是把时间当作一个差不多是实实在在的东西来对待的。我们安排时间、节约时间、浪费时间、挤抢时间、消磨时间、缩减时间、对时间的利用作出解释;我们还要因付出时间而收取费用。时间是一种宝贵的资源,许多人都深感人生的短暂。时光一去不复返。我们应当让每一分钟都过得有意义。 Para. 3 外国人对美国的第一印象很可能是:每个人都匆匆忙忙——常常处于压力之下。城里人看上去总是在匆匆地赶往他们要去的地方,在商店里他们焦躁不安地指望店员能马上来为他们服务,或者为了赶快买完东西,用肘来推搡他人。白天吃饭时人们也都匆匆忙忙,这部分地反映出这个国家的生活节奏。工作时间被认为是宝贵的。Para. 3b 在公共用餐场所,人们都等着别人吃完后用餐,以便按时赶回去工作。你还会发现司机开车很鲁莽,人们推搡着在你身边过去。你会怀念微笑、简短的交谈以及与陌生人的随意闲聊。不要觉得这是针对你个人的,这是因为人们非常珍惜时间,而且也不喜欢他人“浪费”时间到不恰当的地步。 Para. 4 许多刚到美国的人会怀念诸如商务拜访等场合开始时的寒暄。他们也会怀念那种一边喝茶或咖啡一边进行的礼节性交流,这也许是他们自己国家的一种习俗。他们也许还会怀念在饭店或咖啡馆里谈生意时的那种轻松悠闲的交谈。一般说来,美国人是不会在如此轻松的环境里通过长时间的闲聊来评价他们的客人的,更不用说会在增进相互间信任的过程中带他们出去吃饭,或带他们去打高尔夫球。既然我们通常是通过工作而不是社交来评估和了解他人,我们就开门见山地谈正事。因此,时间老是在我们心中的耳朵里滴滴答答地响着。 Para. 5 因此,我们千方百计地节约时间。我们发明了一系列节省劳力的装置;我们通过发传真、打电话或发电子邮件与他人迅速地进行交流,而不是通过直接接触。虽然面对面接触令人愉快,但却要花更多的时间, 尤其是在马路上交通拥挤的时候。因此,我们把大多数个人拜访安排在下班以后的时间里或周末的社交聚会上。 Para. 6 就我们而言,电子交流的缺乏人情味与我们手头上事情的重要性之间很少有或完全没有关系。在有些国家, 如果没有目光接触,就做不成大生意,这需要面对面的交谈。在美国,最后协议通常也需要本人签字。然而现在人们越来越多地在电视屏幕上见面,开远程会议不仅能解决本国的问题,而且还能通过卫星解决国际问题。
新视野大学英语3第三版课文翻译 Unit 1 The Way to Success 课文A Never, ever give up! 永不言弃! As a young boy, Britain's great Prime Minister, Sir Winston Churchill, attended a public school called Harrow. He was not a good student, and had he not been from a famous family, he probably would have been removed from the school for deviating from the rules. Thankfully, he did finish at Harrow and his errors there did not preclude him from going on to the university. He eventually had a premier army career whereby he was later elected prime minister. He achieved fame for his wit, wisdom, civic duty, and abundant courage in his refusal to surrender during the miserable dark days of World War II. His amazing determination helped motivate his entire nation and was an inspiration worldwide. Toward the end of his period as prime minister, he was invited to address the patriotic young boys at his old school, Harrow. The headmaster said, "Young gentlemen, the greatest speaker of our time, will be here in a few days to address you, and you should obey whatever sound advice he may give you." The great day arrived. Sir Winston stood up, all five feet, five inches and 107 kilos of him, and gave this short, clear-cut speech: "Young men, never give up. Never give up! Never give up! Never, never, never, never!" 英国的伟大首相温斯顿·丘吉尔爵士,小时候在哈罗公学上学。当时他可不是个好学生,要不是出身名门,他可能早就因为违反纪律被开除了。谢天谢地,他总算从哈罗毕业了,在那里犯下的错误并没影响到他上大学。后来,他凭着军旅生涯中的杰出表现当选为英国首相。他的才思、智慧、公民责任感以及在二战痛苦而黑暗的时期拒绝投降的无畏勇气,为他赢得了美名。他非凡的决心,不仅激励了整个民族,还鼓舞了全世界。 在他首相任期即将结束时,他应邀前往母校哈罗公学,为满怀报国之志的同学们作演讲。校长说:“年轻的先生们,当代最伟大的演说家过几天就会来为你们演讲,他提出的任何中肯的建议,你们都要听从。”那个激动人心的日子终于到了。温斯顿爵士站了起来——他只有5 英尺5 英寸高,体重却有107 公斤。他作了言简意赅的讲话:“年轻人,要永不放弃。永不放弃!永不放弃!永不,永不,永不,永不!” Personal history, educational opportunity, individual dilemmas - none of these can inhibit a strong spirit committed to success. No task is too hard. No amount of preparation is too long or too difficult. Take the example of two of the most scholarly scientists of our age, Albert Einstein and Thomas Edison. Both faced immense obstacles and extreme criticism. Both were called "slow to learn" and written off as idiots by their teachers. Thomas Edison ran away from school because his teacher whipped him repeatedly for asking too many questions. Einstein didn't speak fluently until he was almost nine years old and was such a poor student that some thought he was unable to learn. Yet both boys' parents believed in them. They worked intensely each day with their sons, and the boys learned to never bypass the long hours of hard work that they needed to succeed. In the end, both Einstein and Edison overcame their childhood persecution and went on to achieve magnificent discoveries that benefit the entire world today. Consider also the heroic example of Abraham Lincoln, who faced substantial hardships, failures and repeated misfortunes in his lifetime. His background was certainly not glamorous. He was raised in a very poor family with only one year of formal education. He failed in business twice, suffered a nervous breakdown when his first love died suddenly and lost eight political
Text A 课文 A The humanities: Out of date? 人文学科:过时了吗? When the going gets tough, the tough takeaccounting. When the job market worsens, manystudents calculate they can't major in English orhistory. They have to study something that booststheir prospects of landing a job. 当形势变得困难时,强者会去选学会计。当就业市场恶化时,许多学生估算着他们不能再主修英语或历史。他们得学一些能改善他们就业前景的东西。 The data show that as students have increasingly shouldered the ever-rising c ost of tuition,they have defected from the study of the humanities and toward applied science and "hard"skills that they bet will lead to employment. In oth er words, a college education is more andmore seen as a means for economic betterment rather than a means for human betterment.This is a trend that i s likely to persist and even accelerate. 数据显示,随着学生肩负的学费不断增加,他们已从学习人文学科转向他们相信有益于将来就业的应用科学和“硬”技能。换言之,大学教育越来越被看成是改善经济而不是提升人类自身的手段。这种趋势可能会持续,甚至有加快之势。 Over the next few years, as labor markets struggle, the humanities will proba bly continue theirlong slide in succession. There already has been a nearly 50 percent decline in the portion of liberal arts majors over the past generatio n, and it is logical to think that the trend is boundto continue or even accel erate. Once the dominant pillars of university life, the humanities nowplay li ttle roles when students take their college tours. These days, labs are more vi vid and compelling than libraries. 在未来几年内,由于劳动力市场的不景气,人文学科可能会继续其长期低迷的态势。在上一代大学生中,主修文科的学生数跌幅已近50%。这种趋势会持续、甚至加速的想法是合情合理的。人文学科曾是大学生活的重要支柱,而今在学生们参观校园的时候,却只是一个小点缀。现在,实验室要比图书馆更栩栩如生、受人青睐。 Here, please allow me to stand up for and promote the true value that the h umanities add topeople's lives. 在这儿,请允许我为人文学科给人们的生活所增添的真实价值进行支持和宣传。
第10课 日本的季节 日本的一年有春、夏、秋、冬四个季节。 3月、4月和5月这三个月是春季。春季是个暖和的好季节。桃花、樱花等花儿开得很美。人们在4月去赏花。 6月到8月是夏季。夏季非常闷热。人们去北海道旅游。7月和8月是暑假,年轻人去海边或山上。也有很多人去攀登富士山。富士山是日本最高的山。 9月、10月和11月这3个月是秋季。秋季很凉爽,晴朗的日子较多。苹果、桔子等许多水果在这个季节成熟。 12月到2月是冬季。日本的南部冬天不太冷。北部非常冷,下很多雪。去年冬天东京也很冷。今年大概不会那么冷吧。如果冷的话,人们就使用暖气炉。 第12课 乡下 我爷爷住哎乡下。今天,我要去爷爷家。早上天很阴,但中午天空开始变亮,天转好了。我急急忙忙吃完午饭,坐上了电车。 现在,电车正行驶在原野上。窗外,水田、旱地连成一片。汽车在公路上奔驰。 这时,电车正行驶在大桥上。下面河水在流动。河水很清澈,可以清澈地看见河底。可以看见鱼在游动。远处,一个小孩在挥手。他身旁,牛、马在吃草。 到了爷爷居住的村子。爷爷和奶奶来到门口等着我。爷爷的房子是旧房子,但是很大。登上二楼,大海就在眼前。海岸上,很多人正在全力拉缆绳。渐渐地可以看见网了。网里有很多鱼。和城市不同,乡下的大自然真是很美。 第13课 暑假 大概没有什么比暑假更令学生感到高兴的了。大学在7月初,其他学校在二十四日左右进入暑假。暑假大约1个半月。 很多人利用这个假期去海边、山上,或者去旅行。学生中,也有人去打工。学生由于路费等只要半价,所以在学期间去各地旅行。因此,临近暑假时,去北海道的列车上就挤满了这样的人。从炎热的地方逃避到凉爽的地方去,这是很自然的事。一般在1月、最迟在2月底之前就要预定旅馆。不然的话可能会没有地方住。 暑假里,山上、海边、湖里、河里会出现死人的事,这种事故都是由于不注意引起的。大概只能每个人自己多加注意了。 在东京附近,镰仓等地的海面不起浪,因此挤满了游泳的人。也有人家只在夏季把海边的房子租下来。 暑假里,学校的老师给学生布置作业,但是有的学生叫哥哥或姐姐帮忙。 第14课 各式各样的学生 我就读的大学都有各种各样的学生入学。学生有的是中国人,有的是美国人,有的是英国人。既有年轻的,也有不年轻的。有胖的学生,也有瘦的学生。学生大多边工作边学习。因此,大家看上去都很忙。经常有人边听课边打盹。 我为了学习日本先进的科学技术和日本文化来到日本。预定在这所大学学习3年。既然特意来了日本,所以每天都很努力学习。即便如此,考试之前还是很紧张。其他学生也是这
教育界的科技革命 如果让生活在年的人来到我们这个时代,他会辨认出我们当前课堂里发生的许多事情——那盛行的讲座、对操练的强调、从基础读本到每周的拼写测试在内的教学材料和教学活动。可能除了教堂以外,很少有机构像主管下一代正规教育的学校那样缺乏变化了。 让我们把上述一贯性与校园外孩子们的经历作一番比较吧。在现代社会,孩子们有机会接触广泛的媒体,而在早些年代这些媒体简直就是奇迹。来自过去的参观者一眼就能辨认出现在的课堂,但很难适应现今一个岁孩子的校外世界。 学校——如果不是一般意义上的教育界——天生是保守的机构。我会在很大程度上为这种保守的趋势辩护。但变化在我们的世界中是如此迅速而明确,学校不可能维持现状或仅仅做一些表面的改善而生存下去。的确,如果学校不迅速、彻底地变革,就有可能被其他较灵活的机构取代。 计算机的变革力 当今时代最重要的科技事件要数计算机的崛起。计算机已渗透到我们生活的诸多方面,从交通、电讯到娱乐等等。许多学校当然不能漠视这种趋势,于是也配备了计算机和网络。在某种程度上,这些科技辅助设施已被吸纳到校园生活中,尽管他们往往只是用一种更方便、更有效的模式教授旧课程。 然而,未来将以计算机为基础组织教学。计算机将在一定程度上允许针对个人的授课,这种授课形式以往只向有钱人提供。所有的学生都会得到符合自身需要的、适合自己学习方法和进度的课程设置,以及对先前所学材料、课程的成绩记录。 毫不夸张地说,计算机科技可将世界上所有的信息置于人们的指尖。这既是幸事又是灾难。我们再也无须花费很长时间查找某个出处或某个人——现在,信息的传递是瞬时的。不久,我们甚至无须键入指令,只需大声提出问题,计算机就会打印或说出答案,这样,人们就可实现即时的"文化脱盲"。 美中不足的是,因特网没有质量控制手段;"任何人都可以拨弄"。信息和虚假信息往往混杂在一起,现在还没有将网上十分普遍的被歪曲的事实和一派胡言与真实含义区分开来的可靠手段。要识别出真的、美的、好的信息,并挑出其中那些值得知晓的, 这对人们构成巨大的挑战。 对此也许有人会说,这个世界一直充斥着错误的信息。的确如此,但以前教育当局至少能选择他们中意的课本。而今天的形势则是每个人都拥有瞬时可得的数以百万计的信息源,这种情况是史无前例的。 教育的客户化 与以往的趋势不同,从授权机构获取证书可能会变得不再重要。每个人都能在模拟的环境中自学并展示个人才能。如果一个人能像早些时候那样"读法律",然后通过计算机模拟的实践考试展现自己的全部法律技能,为什么还要花万美元去上法学院呢?用类似的方法学开飞机或学做外科手术不同样可行吗? 在过去,大部分教育基本是职业性的:目的是确保个人在其年富力强的整个成人阶段能可靠地从事某项工作。现在,这种设想有了缺陷。很少有人会一生只从事一种职业;许多人都会频繁地从一个职位、公司或经济部门跳到另一个。 在经济中,这些新的、迅速变换的角色的激增使教育变得大为复杂。大部分老成持重的教师和家长对帮助青年一代应对这个会经常变换工作的世界缺乏经验。由于没有先例,青少年们只有自己为快速变化的"事业之路"和生活状况作准备。