
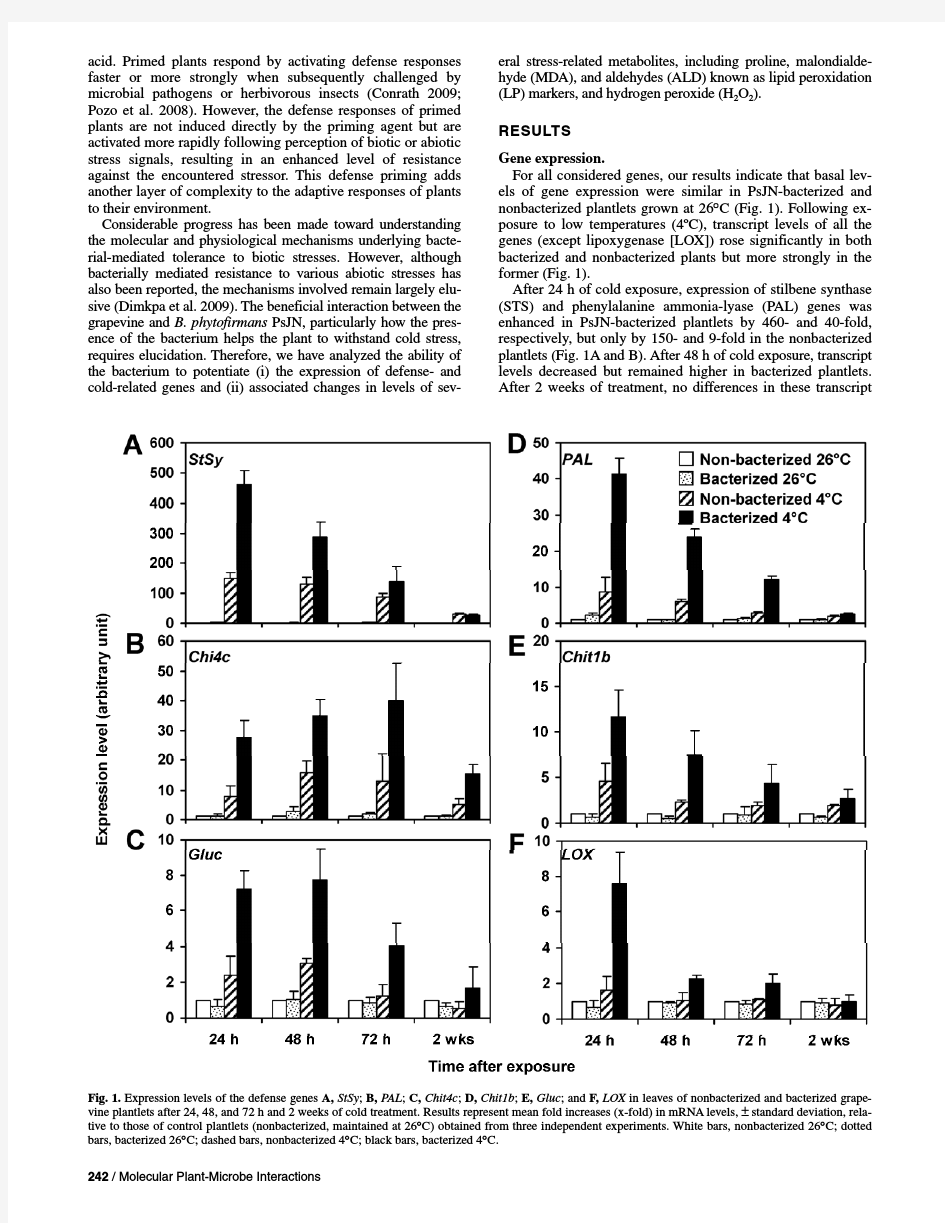
用Prim算法构造最小生成树 班级:2010级计算机1班学号:2010131116 姓名:杨才一、实验目的 了解最小生成树的概念,掌握生成最小生成树的方法。 二、实验内容 建立一个含任意结点的无向连通网,并用Prim算法构造其最小生成树 三、实验要点及说明 如果无向连通图是一个网,则其所有生成树中必有一棵树的边的权值总和最小,这棵生成树为最小生成树。 Prim算法:在图G=(V,E)(V为顶点集,E为边集)中任选一顶点v0,令集合U={v0}为初态,在一个顶点在U中,另一顶点在V-U 中的所有边中找权值最小的边(u,v)(U∈ u,v∈ V-U),并将v加入到U中,同时将边(u,v)加入集合T中(T的初态为空集),这样不断地扩大U,直至U=V,则集合T中的边为所求最小生成树的边 四、算法思想与算法描述 1、邻接矩阵的数据类型的定义如下: typedef struct { int no; /*顶点编号*/ string name; /*顶点其他信息*/ } VertexType; /*顶点类型*/ typedef struct/*图的定义*/ { int edges[MAXV][MAXV]; /*邻接矩阵*/ int vexnum,arcnum; /*顶点数,弧数*/ VertexType vexs[MAXV]; /*存放顶点信息*/ }MGraph; 2、临时数组的存放的数据类型 struct { int closest; // U集中的顶点序号 int lowcost; // 边的权值 } closedge[MAXV]; int const INF=32767; /*INF表示∞*/ 3、prime算法实现:(原理见实验说明) void prime(MGraph g,int v) { int lowcost[MAXV]; int min; int closest[MAXV]; int i,j,k; for(i=0;i :算法的设计思想 本算法采用分支定界算法实现。构造解空间树为:第一个城市为根结点,与第一个城市相邻的城市为根节点的第一层子节点,依此类推;每个父节点的子节点均是和它相邻的城市;并且从第一个根节点到当前节点的路径上不能出现重复的城市。 本算法将具有最佳路线下界的节点作为最有希望的节点来展开解空间树,用优先队列实现。算法的流程如下:从第一个城市出发,找出和它相邻的所有城市,计算它们的路线下界和费用,若路线下界或费用不满足要求,将该节点代表的子树剪去,否则将它们保存到优先队列中,并选择具有最短路线下界的节点作为最有希望的节点,并保证路径上没有回路。当找到一个可行解时,就和以前的可行解比较,选择一个较小的解作为当前的较优解,当优先队列为空时,当前的较优解就是最优解。算法中首先用Dijkstra算法算出所有点到代表乙城市的点的最短距离。算法采用的下界一个是关于路径长度的下界,它的值为从甲城市到当前城市的路线的长度与用Dijkstra算法算出的当前城市到乙城市的最短路线长度的和;另一个是总耗费要小于1500。 伪代码 算法AlgBB() 读文件m1和m2中的数据到矩阵length和cost中 Dijkstra(length) Dijkstra(cost) while true do for i←1 to 50 do //选择和node节点相邻的城市节点 if shortestlength>optimal or mincost>1500 pruning else if i=50 optimal=min(optimal,tmpopt)//选当前可行解和最优解的 较小值做最优解 else if looped //如果出现回路 pruning //剪枝 else 将城市i插入到优先队列中 end for while true do if 优先队列为空 输出结果 else 取优先队列中的最小节点 if 这个最小节点node的路径下界大于当前的较优解 continue 算法分析与设计之Prim 学院:软件学院学号:201421031059 :吕吕 一、问题描述 1.Prim的定义 Prim算法是贪心算法的一个实例,用于找出一个有权重连通图中的最小生成树,即:具有最小权重且连接到所有结点的树。(强调的是树,树是没有回路的)。 2.实验目的 选择一门编程语言,根据Prim算法实现最小生成树,并打印最小生成树权值。 二、算法分析与设计 1.Prim算法的实现过程 基本思想:假设G=(V,E)是连通的,TE是G上最小生成树中边的集合。算法从U ={u0}(u0∈V)、TE={}开始。重复执行下列操作: 在所有u∈U,v∈V-U的边(u,v)∈E中找一条权值最小的边(u0,v0)并入集合TE中,同时v0并入U,直到V=U为止。 此时,TE中必有n-1条边,T=(V,TE)为G的最小生成树。 Prim算法的核心:始终保持TE中的边集构成一棵生成树。 2.时间复杂度 Prim算法适合稠密图,其时间复杂度为O(n^2),其时间复杂度与边得数目无关,N 为顶点数,而看ruskal算法的时间复杂度为O(eloge)跟边的数目有关,适合稀疏图。 三、数据结构的设计 图采用类存储,定义如下: class Graph { private: int *VerticesList; int **Edge; int numVertices; int numEdges; int maxVertices; public: Graph(); ~Graph(); bool insertVertex(const int vertex); bool insertEdge(int v1,int v2,int cost); int getVertexPos(int vertex); int getValue(int i); int getWeight(int v1,int v2); int NumberOfVertices(); 4.3.3实现技术 (1)KKT 条件,工作集选取及停止准则 在求最小包围球的过程中,迭代没有结束前,每轮迭代会有一个新点被选中,核集中加入新的点后,在核集中的点是下面三种情况之一: 1.核向量,满足KKT 条件; 2.处在球内的非核向量,对应的i α为0,也满足KKT 条件; 3.在(,)t t B c R 外面。刚加入进来的点0l α=违反KKT 条件。 加入新的训练点后,参照传统SVM 方法对核集中的样本点检查是否违反KKT 条件的算法推导如下: 原始问题的KKT 条件: 2 2 (||()||)0i i i R c x αξ?+--= (4.16) 加上已知条件 0i i βξ=,0i i C αβ--= 根据i α的不同,有三种情况: ● 0i α=,有22||()||0i i R c x ξ?+--≥,又i C β=,则0i ξ=,因此有 2 2 ||()||i c x R ?-≤ (4.17) ● 0i C α<<,有22||()||0i i R c x ξ?+--=,又0i β>,则0i ξ=,因此有 2 2 ||()||i c x R ?-= (4.18) ● i C α=,有22||()||0i i R c x ξ?+--=,又0i β=,则0i ξ≥,因此有 2 2 ||()||i c x R ?-≥ (4.19) 每次迭代以对KKT 条件破坏最多的两个样本为工作集,因此,选取以下两个样本下标 2 arg m ax(||()|||) i i s c x C ?α=-< 2 arg m in(||()|||0)i i t c x ?α=-> 若记 2 ||()|| s i g c x ?=-,2||()||t i g c x ?=- 算法和流程图 一、学习目的和学习内容 学习各种软件的使用——>让运算机按照我们的意图去完成一件事——>编程序(软件)给别人用; 国际信息学(运算机)奥林匹克竞赛——全国中学生信息学奥赛——江苏省中学生信息学奥赛; 竞赛的内容确实是编程竞赛;这也是我们的学习目的和内容; 运算机程序设计语言:人类语言——>用程序设计语言(如Pascal语言)表示——>再翻译成机器语言; 二、运算机解决问题的步骤 做任何一件事都要有一定的的步骤,如求1+2+3+4+5+6+7+8+9+10; 运算机解题步骤:分析问题 ——>确定解决问题的方法和步骤(即算法) ——>选择一种运算机语言,依照算法编写运算机程序 ——>让运算机执行那个程序获得结果 三、算法的概念 1、为解决某一个问题而采取的方法和步骤,称为算法。或者说算法是解决一个问题的方法的精确描述。 如:已知半径,运算圆的面积的算法。 算法读入半径R的值——>运算圆的面积S=π*R*R——>输出圆的面积S。 注意:算法不一定唯独,如求1+2+3+4+5+6+7+8+9+10的算法。 2、算法的特点: ①有穷性:必须在执行了有穷个运算步骤后终止; ②确定性:每一个步骤必须是精确的、无二义性的; ③可行性:能够用运算机解决、能在有限步、有限时刻内完成; ④有输入: ⑤有输出: 四、算法举例 例一:交换两个大小相同的杯子中的液体(A水、B酒)。 算法1: 1、再找一个大小与A相同的空杯子C; 2、A——>C; 3、B——>A; 4、C——>B;终止。 或(B——>C、A——>B、C——>A) 算法2: 1、再找两个空杯子C和D; 2、A——>C、B——>D; 3、C——>B、D——>A;终止。 莫队算法详解 本文翻译自MO’s Algorithm (Query square root decomposition),作者anudeep2011,发表日期为2014-12-28。由于最近碰到一些莫队算法的题目,找到的相关中文资料都比较简略,而这篇英语文章则讲解的比较详细,故翻译成中文与大家分享。由于本人水平有限,错误在所难免,请谅解。下面是译文。 我又发现了一个有用,有趣但网上资源非常少的话题。在写作之前,我做了一个小调查,令我惊讶的是,几乎所有的印度程序员都不知道该算法。学习这个很重要,事实上所有的codeforces 红名程序员都使用这个算法,比如在div 1 C 题和D 题中。在一年半以前没有这方面的题目,但从那时起这类题目的数量就爆发了!我们可以期待这在未来的比赛中会有更多的这类题目。 莫队算法详解 问题描述 复杂度的简单的解法 一个解决上述问题的算法及其正确性对上述算法的复杂性证明 - 上述算法的适用范围 习题和示例代码 问题描述 给定一个大小为N 的数组,数组中所有元素的大小<=N 。你需要回答M 个查询。每个查询的形式是L ,R 。你需要回答在范围[ L ,R ]中至少重复3次的数字的个数。 例如:数组为{ 1,2,3,1,1,2,1,2,3,1 }(索引从0开始) 查询:L = 0,R = 4。答案= 1。在范围[L ,R]中的值 = { 1,2,3,1,1 },只有1是至少重复3次的。 查询:L = 1, R = 8。答案= 2。在范围[L ,R]中的值 = { 2,3,1,1,2,1,2,3 }, 1重复3遍并且2重复3次。至少重复3次的元素数目=答案= 2。 复杂度的简单的解法 对于每一个查询,从L 至R 循环,统计元素出现频率,报告答案。考虑M = N 的情况,以下程序在最 O ()N 2O (?N ) N ??√O ()N 2 2 /*分别利用prim算法和kruskal算法实现求图的最小生成树*/ #include if(i==j) GA[i][j]=0; else GA[i][j]=MaxValue; printf("输入%d条无向带权边",e); for(k=0;k xx学院 《数据结构与算法》课程设计 报告书 课程设计题目 PRIM算法求最小生成树 院系名称计算机科学与技术系 专业(班级) 姓名(学号) 指导教师 完成时间 一、问题分析和任务定义 在该部分中主要包括两个方面:问题分析和任务定义; 1 问题分析 本次课程设计是通过PRIM(普里姆)算法,实现通过任意给定网和起点,将该网所对应的所有生成树求解出来。 在实现该本设计功能之前,必须弄清以下三个问题: 1.1 关于图、网的一些基本概念 1.1.1 图图G由两个集合V和E组成,记为G=(V,E),其中V是顶点的有穷非空集合,E是V中顶点偶对的有穷集,这些顶点偶对称为边。通常,V(G)和E(G)分别表示图G的顶点集合和边集合。E(G)也可以为空集。则图G只有顶点而没有边。1.1.2 无向图对于一个图G,若边集E(G)为无向边的集合,则称该图为无向图。1.1.3 子图设有两个图G=(V,E)G’=(V’,),若V’是V的子集,即V’?V ,且E’是E的子集,即E’?E,称G’是G的子图。 1.1.4 连通图若图G中任意两个顶点都连通,则称G为连通图。 1.1.5 权和网在一个图中,每条边可以标上具有某种含义的数值,该数值称为该边的权。把边上带权的图称为网。如图1所示。 1.2 理解生成树和最小生成树之间的区别和联系 1.2.1 生成树在一个连通图G中,如果取它的全部顶点和一部分边构成一个子图G’,即:V(G’)= V(G)和E(G’)?E(G),若边集E(G’)中的边既将图中的所有顶点连通又不形成回路,则称子图G’是原图G的一棵生成树。 1.2.2 最小生成树图的生成树不是唯一的,把具有权最小的生成树称为图G的最小生成树,即生成树中每条边上的权值之和达到最小。如图1所示。 图1.网转化为最小生成树 1.3 理解PRIM(普里姆)算法的基本思想 1.3.1 PRIM算法(普里姆算法)的基本思想假设G =(V,E)是一个具有n个顶点的连通网,T=(U,TE)是G的最小生成树,其中U是T的顶点集,TE是T的边集,U和TE的初值均为空集。算法开始时,首先从V中任取一个顶点(假定取V0),将它并入U中,此时U={V0},然后只要U是V的真子集,就从那些其一个端点已在T中,另一个端点仍在T外的所有边中,找一条最短(即权值最小)边,假定为(i,j),其中V i∈U,V j∈(V-U),并把该边(i,j)和顶点j分别并入T的边集TE和顶点集U,如此进行下去,每次往生成树里并入一个顶点和一条边,直到n-1次后就把所有n个顶点都并入到生成树T的顶点集中,此时U=V,TE中含有n-1条边,T就是最后得到的最小生成树。可以看出,在普利姆算法中,是采用逐步增加U中的顶点,常称为“加点法”。为了实现这个算法在本设计中需要设置一个辅助数组 1.无向网图及其邻接矩阵存储示意图 0 34 56 999 999 34 arc[ 6][6]= 34 0 58 999 50 999 56 58 0 76 13 30 999 999 76 0 63 48 999 50 13 63 0 999 34 56 999 999 34 0 2.Prim()算法构造最小生成树过程 1).连通网U={南京} cost={(南京,上海)18,(南京,北京)56,(南京,南昌)999,(南京,天津)999,(南京,徐州)34} 2).U={南京,上海} cost={(南京,北京)56,(南京,南昌)999,(上海,天津)50,(南京,徐州)34} 3).U={南京,上海,天津} cost={(天津,北京)13,(天津,南昌)63,(南京,徐州)34} 4).U={南京,上海,天津,北京} cost={(天津,南昌)63,(北京,徐州)30} 5).U={南京,上海,天津,北京,徐州} cost={(徐州,南昌)48} 6).U={南京,上海,天津,北京,徐州,南昌} cost={} 南京 上海 北京 南昌 天津 徐州 76 48 63 13 30 50 58 18 34 56 南京 上海 南昌 天津 徐州 北京 3.Prim算法构造最小生成树过程中参数变化 南京:v0 上海:v1 北京:v2 南昌:v3 天津:v4 徐州:v5 顶点集 数组 shortEdge 南京上海北京南昌天津徐州U 输出 adjvex lowcost 0 0 0 0 0 0 {v0} {v0,v1} 0 1856 999 999 34 adjvex lowcost 0 0 0 0 1 0 {v0,v1} {v1,v4} 0 0 56 999 5034 adjvex lowcost 0 0 4 4 1 0 {v0,v1,v4} {v4,v2} 0 0 1363 0 34 adjvex lowcost 0 0 4 5 1 2 {v0,v1,v4,v2} {v2,v5} 0 0 0 48 0 30 adjvex lowcost 0 0 4 5 1 2 {v0,v1,v4,v2,v5} {v5,v3} 0 0 0 480 0 adjvex lowcost 0 0 4 3 1 2 {v0,v1,v4,v2,v5,v3} 0 0 0 0 0 0 4.程序主要代码 /***********构造函数***********/ //设置的固定的值方便调试 template 程序算法描述流程图 程序算法描述流程图 算法的方法 递推法 递推是序列计算机中的一种常用算法。它是按照一定的规律来计算序列中的每个项,通常是通过计算机前面的一些项来得出序列中的指定项的值。其思想是把一个复杂的庞大的计算过程转化为简单过程的多次重复,该算法利用了计算机速度快和不知疲倦的机器特点。 递归法 程序调用自身的编程技巧称为递归(recursion)。一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说,递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。 注意: (1) 递归就是在过程或函数里调用自身; (2) 在使用递归策略时,必须有一个明确的递归结束条件,称为递归出口。 穷举法 穷举法,或称为暴力破解法,其基本思路是:对于要解决的问题,列举出它的所有可能的情况,逐个判断有哪些是符合问题所要求的条件,从而得到问题的解。它也常用于对于密码的破译,即将密码进行逐个推算直到找出真正的密码为止。例如一个 已知是四位并且全部由数字组成的密码,其可能共有10000种组合,因此最多尝试10000次就能找到正确的密码。理论上利用这种方法可以破解任何一种密码,问题只在于如何缩短试误时间。因此有些人运用计算机来增加效率,有些人辅以字典来缩小密码组合的范围。 贪心算法 贪心算法是一种对某些求最优解问题的更简单、更迅速的设计技术。 用贪心法设计算法的特点是一步一步地进行,常以当前情况为基础根据某个优化测度作最优选择,而不考虑各种可能的整体情况,它省去了为找最优解要穷尽所有可能而必须耗费的大量时间,它采用自顶向下,以迭代的方法做出相继的贪心选择,每做一次贪心选择就将所求问题简化为一个规模更小的子问题, 通过每一步贪心选择,可得到问题的一个最优解,虽然每一步上都要保证能获得局部最优解,但由此产生的全局解有时不一定是最优的,所以贪婪法不要回溯。 贪婪算法是一种改进了的分级处理方法,其核心是根据题意选取一种量度标准,然后将这多个输入排成这种量度标准所要求的顺序,按这种顺序一次输入一个量,如果这个输入和当前已构成在这种量度意义下的部分最佳解加在一起不能产生一个可行解,则不把此输入加到这部分解中。这种能够得到某种量度意义下最优解的分级处理方法称为贪婪算法。 对于一个给定的问题,往往可能有好几种量度标准。初看起来,这些量度标准似乎都是可取的,但实际上,用其中的大多数量度标准作贪婪处理所得到该量度意义下的最优解并不是问题的最优解,而是次优解。因此,选择能产生问题最优解的最优量度标准是使用贪婪算法的核心。 一般情况下,要选出最优量度标准并不是一件容易的事,但对某问题能选择出最优量度标准后,用贪婪算法求解则特别有效。 算法与程序框图 一、程序框图与算法基本逻辑结构: 1.程序框图符号及作用: 程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形. 例:解一元二次方程:2 0(0)ax bx c a ++=≠ 2.画程序框图的规则: 为了使大家彼此之间能够读懂各自画出的框图,必须遵守一些共同的规则,下面对一些常用的规则做一简要介绍. (1)实用标准的框图符号. (2)框图一般按从上到下、从左到右的方向画. (3)一个完整的程序框图必须有终端框,用于表示程序的开始和结束. (4)除判断框外,大多数框图符号只有一个进入点和一个退出点,判断框是具有超过一个退出点的唯一符号,另外,一种判断框是“是”与“不是”两分支的判断,而且有且仅有两个结果;还有一种是多分支判断,有几个不同的结果. 3.算法的三种基本逻辑结构: (1)顺序结构 顺序结构是最简单的算法结构,语句与语句之间, 框与框之间是按从上到下的顺序进行的,它是由 若干个依次执行的处理步骤组成的,它是任何一 个算法离不开的基本结构.如图,只有在执行完步 骤n 后,才能接着执行步骤n+1. 例:.已知梯形的上底、下底和高分别为5、8、9,写出求梯形的面积的算法,画出流程图. 解:算法如下: S1 a ←5; S2 b ←8; S3 h ←9; S4 S ←(a +b )×h /2; S5 输出S . 流程图如下: (2)条件结构 一些简单的算法可以用顺序结构来实现,顺序结构中所表达的逻辑关系是自然串行,线性排列的.但这种结构无法描述逻辑判断,并根据判断结果进行不同的处理的操作,(例如遇到十字路口看信号灯过马路的问题)因此,需要另一种逻辑结构来处理这类问题. 条件结构的结构形式如图,在此结构中含有一个判断框,算法执行到此判断框给定的条件P 时,根据条件P 是否成立,选择不同的执行框(步骤A ,步骤B ),无论条件P 是否成立,只能执行步骤A 或步骤B 之一,不可以两者都执行或都不执行.步骤A 和步骤B 中可以有一个是空的. 例:某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为 0.53,50, 500.53(50)0.85, 50, c ωωωω?≤?=? ?+-?>?其中ω(单位:kg )为行李的重量. 试给出计算费用c (单位:元)的一个算法,并画出流程图. 1S 输入行李的重量ω; 2S 如果50ω≤,那么0.53c ω=?, 否则500.53(50)0.85c ω=?+-?; 3S 输出行李的重量ω和运费c . 步骤n 步骤n+1 ↓ ↓ ↓ 开始结束b h a 5 89 S (+)×/2a b h 输出S 满足条件? 步骤A 步骤B 是否 满足条件? 步骤A 是否 Java基础算法详解 查找和排序算法是算法的入门知识,其经典思想可以用于很多算法当中。因为其实现代码较短,应用较常见。所以在面试中经常会问到排序算法及其相关的问题。但万变不离其宗,只要熟悉了思想,灵活运用也不是难事。一般在面试中最常考的是快速排序和归并排序,并且经常有面试官要求现场写出这两种排序的代码。对这两种排序的代码一定要信手拈来才行。还有插入排序、冒泡排序、堆排序、基数排序、桶排序等。 面试官对于这些排序可能会要求比较各自的优劣、各种算法的思想及其使用场景。还有要会分析算法的时间和空间复杂度。通常查找和排序算法的考察是面试的开始,如果这些问题回答不好,估计面试官都没有继续面试下去的兴趣都没了。所以想开个好头就要把常见的排序算法思想及其特点要熟练掌握,有必要时要熟练写出代码。 冒泡排序 冒泡排序是最简单的排序之一了,其大体思想就是通过与相邻元素的比较和交换来把小的数交换到最前面。这个过程类似于水泡向上升一样,因此而得名。举个栗子,对5,3,8,6,4这个无序序列进行冒泡排序。首先从后向前冒泡,4和6比较,把4交换到前面,序列变成5,3,8,4,6。同理4和8交换,变成5,3,4,8,6,3和4无需交换。5和3交换,变成3,5,4,8,6,3.这样一次冒泡就完了,把最小的数3排到最前面了。对剩下的序列依次冒泡就会得到一个有序序列。冒泡 排序的时间复杂度为O(n^2)。 实现代码: *@Description:冒泡排序算法实现 public class BubbleSort { public static void bubbleSort(int[] arr) { if(arr == null || arr.length == 0) for(int i=0; i) { for(int j=arr.length-1; ji; j--) { if(arr[j]arr[j-1]) { swap(arr, j-1, j); public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; 抑或简单理解一点的正向排序 public class BubbleSort { public static void bubbleSort(int[] arr) { if(arr == null || arr.length == 0) for(int i=1;iarr.length-1;i++) { for(int j=0; jarr.length-i; j++) { if(arr[j]arr[j+1]) { swap(arr, j+1, j); 概率流程图的数学计算 授课对象:高二 授课内容:算法流程图、排列组合、统计 一、知识回顾 算法流程图的组成元素、画法、代码、秦九韶算法 例1 任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判定。 例2 用二分法设计一个求议程x2–2=0的近似根的算法。 已知x=4,y=2,画出计算w=3x+4y的值的程序框图。 解:程序框如下图所示: 2 4和2分别是x和y的值 分类加法计数原理、分步乘法计数原理 分类加法计数原理,是什么?怎么用? 核心:每法皆可完成,方法可分类 分步乘法计数原理,是什么?怎么用? 核心:每法皆分步,每步皆未完 排列 排头与非排头 二、课堂讲解 1.排列组合 组合的定义,组合数公式 例:从10个不同颜色的球里面选2个,有多少种情况 二者的区别与关系 2.统计学 简单随机抽样 (1)简单随机抽样要求被抽取的样本的总体个数N是有限的。 (2)简单随机样本数n小于等于样本总体的个数N。 (3)简单随机样本是从总体中逐个抽取的。 (4)简单随机抽样是一种不放回的抽样。 (5)简单随机抽样的每个个体入样的可能性均为n/N。 为了了解全校240名学生的身高情况,从中抽取40名学生进行测量,下列说法正确的是 A.总体是240 B、个体是每一个学生 C、样本是40名学生 D、样本容量是40 分层抽样 (1)分层需遵循不重复、不遗漏的原则。 (2)抽取比例由每层个体占总体的比例确定。 (3)各层抽样按简单随机抽样进行。 某高中共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采 用分层抽样抽取容量为45的样本,那么高一、高二、高三各年级抽取的人数分别为 A.15,5,25 B.15,15,15 C.10,5,30 D15,10,20 某中学高一年级有学生600人,高二年级有学生450人,高三年级有学生750人,每 个学生被抽到的可能性均为0.2,若该校取一个容量为n的样本,则n= 。 系统抽样 下列抽样中不是系统抽样的是() A、从标有1~15号的15号的15个小球中任选3个作为样本,按从小号到 大号排序,随机确定起点i,以后为i+5, i+10(超过15则从1再数起)号入样 B工厂生产的产品,用传关带将产品送入包装车间前,检验人员从传送带上每隔五分钟抽一件产品检验 C、搞某一市场调查,规定在商场门口随机抽一个人进行询问,直到调查到事先规定 的调查人数为止 D、电影院调查观众的某一指标,通知每排(每排人数相等)座位号为14的观众留下 来座谈 从忆编号为1~50的50枚最新研制的某种型号的导弹中随机抽取5枚来进行发射实验, 若采用每部分选取的号码间隔一样的系统抽样方法,则所选取5枚导弹的编号可能是 A.5,10,15,20,25 B、3,13,23,33,43 C.1,2,3,4,5 D、2,4,6,16,32 统计图表:条形图,折线图,饼图,茎叶图 频率分布直方图 为了了解高一学生的体能情况,某校抽取部分学 生进行一分钟跳绳次数次测试,将所得数据整理 后,画出频率分布直方图(如图),图中从左到右 各小长方形面积之比为2:4:17:15:9:3, 第二小组频数为12. (1)第二小组的频率是多少?样本容量是多 少? (2)若次数在110以上(含110次)为达标,试 估计该学校全体高一学生的达标率是多 少? Prim 算法和Kruskal 算法的Matlab 实现 连线问题应用举例: 欲铺设连接n 个城市的高速公路,若i 城与j 城之间的高速公路造价为ij C ,试设计一个线路图,使总的造价最低。 连线问题的数学模型就是图论中在连通的赋权图上求权最小的支撑树。试用Matlab 分别实现求最小支撑数的Prim 算法和Krusal 算法(避圈法)。 一.基本要求: (1) 画出程序流程图; (2) 对关键算法、变量和步骤进行解释说明; (3) 用如下两图对所写算法的正确性进行验证。即输入图的信息,输出对应图 的最小支撑树及其权值。 v 1 v 74 5 v 216 19 6 6 11 2183020 51514 9241 67 53 48 44 (4)分析两种算法的实现复杂度。 二.扩展要求: (1)提供对算法效率(复杂度)进行评估的方法,并通过举例验证,与分析得到的算法复杂度结果相对照; (2)从降低内存消耗、减少计算时间的角度,对算法进行优化。 三.实验步骤 I.用Prim 算法求最小生成树 i .算法分析及需求分析,程序设计 prim 算法的基本思想是:设G=(V ,E )是一个无向连通网,令T=(U ,TE )是G 的最小生成树。T 的初始状态为U={v0}(v0 )TE={},然后重复执行下述操作:在所有u U , v V-U 的边中找一条代价最小的边(u ,v )并入集合TE ,同时v 并入U ,直至U=V 为止。 显然,Prim 算法的基本思想是以局部最优化谋求全局的最优化,而且,还涉及到起始结点的问题。 本程序完成的功能是:从图中的任意结点出发,都能够找出最小生成树 求最短路径算法总结 分类:数据结构 标签: floyd算法 it 部分内容参考 All-Pairs 的最短路径问题:所有点对之间的最短路径 Dijkstra算法是求单源最短路径的,那如果求图中所有点对的最短路径的话则有以下两种解法: 解法一: 以图中的每个顶点作为源点,调用Dijkstra算法,时间复杂度为O(n3); 解法二: Floyd(弗洛伊德算法)更简洁,算法复杂度仍为O(n3)。 n 正如大多数教材中所讲到的,求单源点无负边最短路径用Dijkstra,而求所有点最短路径用Floyd。确实,我们将用到Floyd算法,但是,并不是说所有情况下Floyd都是最佳选择。 对于没有学过Floyd的人来说,在掌握了Dijkstra之后遇到All-Pairs最短路径问题的第一反应可能会是:计算所有点的单源点最短路径,不就可以得到所有点的最短路径了吗。简单得描述一下算法就是执行n次Dijkstra算法。 Floyd可以说是Warshall算法的扩展了,三个for循环便可以解决一个复杂的问题,应该说是十分经典的。从它的三层循环可以看出,它的复杂度是n3,除了在第二层for中加点判断可以略微提高效率,几乎没有其他办法再减少它的复杂度。 比较两种算法,不难得出以下的结论:对于稀疏的图,采用n次Dijkstra比较出色,对于茂密的图,可以使用Floyd算法。另外,Floyd可以处理带负边的图。 下面对Floyd算法进行介绍: Floyd算法的基本思想: 可以将问题分解,先找出最短的距离,然后在考虑如何找出对应的行进路线。如何找出最短路径呢,这里还是用到动态规划的知识,对于任何一个城市而言,i到j的最短距离不外乎存在经过i与j之间的k和不经过k两种可能,所以可以令k=1,2,3,...,n(n是城市的数目),在检查d(ij)与d(ik)+d(kj)的值;在此d(ik)与d(kj)分别是目前为止所知道的i到k 与k到j的最短距离,因此d(ik)+d(kj)就是i到j经过k的最短距离。所以,若有d(ij)>d(ik)+d(kj),就表示从i出发经过k再到j的距离要比原来的i到j距离短,自然把i到j的d(ij)重写为d(ik)+d(kj),每当一个k查完了,d(ij)就是目前的i到j的最短距离。重复这一过程,最后当查完所有的k时,d(ij)里面存放的就是i到j之间的最短距离了。 Floyd算法的基本步骤: 定义n×n的方阵序列D-1, D0 , … Dn-1, 初始化:D-1=C D-1[i][j]=边 1. 输人一个数到变量 a ,输出它的绝对值。(要求用单分支和双分支结构分别设计算法) 单分支结构算法: (1) 输入任意数并赋值给变量 a ; (2) 判断a 是否小于0,如果a 小于0 ,取a 的相反数; (3) 输出a 。 双分支结构算法: (1) 输人任意数并赋值给变量 a ; (2) 判断a 是否小于0,如果a 小于0则输出a 的相反数,否则输出 a 。 2. 最值问题: max-x, i —1 i -i+1 /输出乜/ / 输出 a / 单分支结构算法流程图 双分支结构算法流程医 (1 )求输人的两个数中的最大值。 (开始T (3)求输入的十个数中的最大值。 「开始 J x 7 /输応 '」/输出b / ■ /输躬 ] (2 )求输人的三个数中的最大值。 3.循环求和(不同的控制循环方法) 1.求输人20个数的和。 (知道循环次数,可以采用循环变量i来控制循环次数) 计数法 3.对输入的数据求和,当所求的和超过100则停止输入并 输出求和结果(设此题中输人的 数皆为正数)。 (没有指出输人数据的具体个 数,且不能依据对输入数据的值 来控制循环,控制循环的关键就 在于对循环体中变量s 的判断) 2.求输入的若干个学生成绩 的和,输入-1表示结束。 (不能确定次数,可以用 输入的数据的值来进行控 标志法 输出a / / 输呼〃箱単b / / 輸匹 输出如下图形: ********** ********** ********** ********** ********** A,o?o?o?o? o? o?o?o?oeo> o?o?o?o?o> o?o?o?o?o? o ?o?o?o?o?B?o?o?o?c?o ???o?oeo?o ?o ?o?o?o?o ?o ?o?o?o?o ?o ?o?o?o?o c.?o?o?o?o?o o?o?o?o?o??o?o?o?o ?o o*o?o?o?o??oeoooeoeo a o ?o?o?o?o??o?o?o?o?o ?o?o?o*o?o o?o*oeo>o? 最小生成树Prim算法实现的c ++语言,使用邻接矩阵存储边信息。共三个文件。 第一个 #ifndef __PRIM_H__ #define __PRIM_H__ template t (智乐圆入门1) A*(A星)算法(一) 记得好象刚知道游戏开发这一行的时候老师就提到过A星算法,当时自己基础还不行,也就没有去看这方面的资料,前几天找了一些资料,研究了一天,觉的现在网上介绍A星算法的资料都讲的不够详细(因为我下的那个资料基本算是最详细的了- -但是都有一些很重要的部分没有说清楚....),所以我自己重新写一篇讲解A星算法的资料,还是借用其他资料的一些资源.不过转载太多了,只有谢谢原作者了:) 我们将以下图作为地图来进行讲解,图中对每一个方格都进行了编号,其中绿色的方格代表起点,红色的方格代表终点,蓝色的方格代表障碍,我们将用A星算法来寻找一条从起点到终点最优路径,为了方便讲解,本地图规定只能走上下左右4个方向,当你理解了A星算法,8个方向也自然明白 在地图中,每一个方格最基本也要具有两个属性值,一个是方格是通畅的还是障碍,另一个就是指向他父亲方格的指针(相当于双向链表结构中的父结点指针),我们假设方格值为0时为通畅,值为1时为障碍 A星算法中,有2个相当重要的元素,第一个就是指向父亲结点的指针,第二个就是一个OPEN表,第三个就是CLOSE表,这两张表的具体作用我们在后面边用边介绍,第四个就是每个结点的F值(F值相当于图结构中的权值) 而F = H + G;其中H值为从网格上当前方格移动到终点的预估移动耗费。这经常被称为启发式的,可能会让你有点迷惑。这样叫的原因是因为它只是个猜测。我们没办法事先知道路径的长度,因为路上可能存在各种障碍(墙,水,等等)。虽然本文只提供了一种计算H的方法,但是你可以在网上找到很多其他的方法,我们定义H 值为终点所在行减去当前格所在行的绝对值与终点所在列减去当前格所在最短路径流程图及算法详解
Prim最小生成树算法实验报告材料
svdd算法详解
算法和流程图
莫队算法详解
分别利用prim算法和kruskal算法实现求图的最小生成树
PRIM算法求最小生成树
Prim算法说明及图解
程序算法描述流程图.doc
算法与程序框图汇总
线 性 规 划 算 法 详 解
算法流程图、排列组合、统计
Prim算法和Kruskal算法的Matlab实现
Floyd算法详解
算法流程图
最小生成树 Prim算法实现C++
A星算法详解-通俗易懂初学者必看